 |
Определение геометрического очага деформации
|
|
|
|
Дано: марка стали 10; а = 140 мм; hо = 40 мм; hк = 22 мм; f = 0,40; t = 920 °С;
U =  .
.
Очагом деформации при осадке является вся полоса, так как она осаживается одновременно и полностью. Поскольку длина полосы бесконечна, то рассмотрим поперечное сечение полосы.
Оси координат расположим, как показано на рисунке 4. Из рисунка видно, что ось z направлена по высоте заготовки, т.е. по направлению активной силы. Ось у, направленная по длине заготовки, перпендикулярна плоскости чертежа.

Рисунок 4. Геометрический очаг деформации
Штриховой линией на рисунке показано поперечное сечение полосы до осадки, сплошной – после осадки.
Коэффициент высотной деформации:
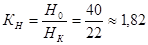 не превышает 2
не превышает 2
Относительная деформация:
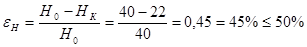
Определение сопротивления металла деформированию
Сопротивление металла деформированию в точке деформируемого тела равно интенсивности напряжений в этой точке, достаточной для осуществления пластической деформации при заданных условиях взаимодействия тела и инструмента.
 (8)
(8)
где 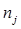 - коэффициент, учитывающий влияние среднего главного напряжения (для плоского деформированного состояния
- коэффициент, учитывающий влияние среднего главного напряжения (для плоского деформированного состояния 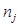 = 1,15);
= 1,15);
 - истинный предел текучести.
- истинный предел текучести.
 (9)
(9)
где 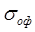 - сопротивление деформированию в линейном напряжённом состоянии;
- сопротивление деформированию в линейном напряжённом состоянии;
 ;
;
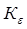 - термомеханический коэффициент, учитывающий влияние обжатия,
- термомеханический коэффициент, учитывающий влияние обжатия,
для стали марки 10 при  :
: 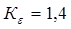 ;
;
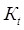 - термомеханический коэффициент, учитывающий влияние температуры,
- термомеханический коэффициент, учитывающий влияние температуры,
для стали марки 10 при  :
:  ;
;
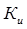 -термомеханический коэффициент, учитывающий влияние скорости деформирования, для стали марки 10 при
-термомеханический коэффициент, учитывающий влияние скорости деформирования, для стали марки 10 при  :
: 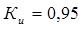 .
.
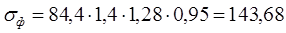 МПа
МПа
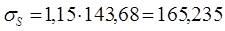 МПа
МПа
Определение контактных напряжений
Контактное напряжение состоит из двух составляющих:
|
|
|
- нормальное касательное напряжение σz,направление вектора которого совпадает с нормалью к площадке приложения сил,
- касательное контактное напряжение τк, действующее в плоскости площадки приложения сил. (см. рисунок 5.)

Рисунок 5. Кинематическая схема при осадке
Направление элементарных сил трения на контактной поверхности, а следовательно, и контактных касательных напряжений показано на рисунок 5. Согласно правилу знаков касательные напряжения на половине фигуры справа от оси будут отрицательны, а слева – положительны. В силу симметрии сечения относительно координатных осей достаточно рассматривать лишь первый квадрант.
Выделим в теле бесконечно малый объём плоскостями, параллельными оси z на расстоянии x и x+dx от начала координат; длину этого объёма примем равной единице.(см. рисунок 6). На выделенный объём действуют нормальные напряжения σz, σx, σx+dσx и касательное напряжение τxz. Согласно второму допущению принимаем, что σz и σx не зависят от координаты z, т.е. постоянны по высоте и зависят только от координаты x. Тогда второе дифференциальное уравнение равновесия
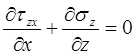 тождественно обращается в нуль.
тождественно обращается в нуль.

Рисунок 6. Схема к определению усилия осадки
Касательное напряжение τxz, переменное по ширине и высоте, на контактной поверхности равно τк - касательному напряжению, обусловленному
трением тела об инструмент. Величина уменьшается при удалении от контактной поверхности и вследствие симметрии на середине высоты полосы равна нулю. Примем, что τxz зависит от высоты полосы линейно, т.е.
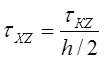 . (10)
. (10)
Тогда 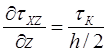 . (11)
. (11)
Подставив значение 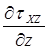 в первое уравнение равновесия, получим:
в первое уравнение равновесия, получим:
 (12)
(12)
Так как касательное напряжение на контактной поверхности обусловлено трением металла об инструмент, естественно его определить на основании закона Кулона - Амонтона:
|
|
|
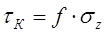 (13)
(13)
Тогда  (14)
(14)
Уравнение пластичности для плоского деформированного состояния для нашего случая представим в виде:
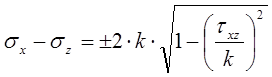 (15)
(15)
Разность нормальных напряжений зависит от касательного напряжения.
Если касательное контактное напряжение не зависит от нормальных напряжений, то разность нормальных напряжений – величина постоянная. В частных случаях, когда τк и τxz равны нулю (трение отсутствует), σx и σz являются главными напряжениями и выражение (15) превращается в уравнение (6):
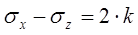 (16)
(16)
Когда τк достигнет максимальной величины k, уравнение (15) получит вид:
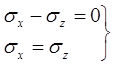 (17)
(17)
Дифференцируя уравнения (6) и (17), получаем уравнение пластичности в дифференциальной форме:
 (18)
(18)
точное при указанных выше условиях постоянства или независимости τк от σx и σz.
Если τк зависит от нормального напряжения σz, как в нашем случае, при изменении τк от нуля до 0,7k для приближённых расчётов можно пользоваться уравнением пластичности в форме (6), а при 0,7k < τк ≤ k - в форме (15). Тогда выражение (17) является приближённым.
Подставив выражения (13) и (18) в уравнение (12), получим:
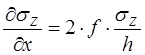 (19)
(19)
После разделения переменных и интегрирования находим:
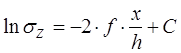 (20)
(20)
Отсюда
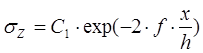 (21)
(21)
Постоянную интегрирования C1 определим из граничного условия (при x=b, σz = -β∙σт = - σт):
 (22)
(22)
Следовательно,
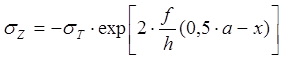 (23)
(23)
 (24)
(24)
По формуле (23) можно определить σz в любой точке контактной поверхности.
Зона скольжения – участок где металл скользит по инструменту, контактное касательное напряжение является напряжением трения скольжения и подчиняется закону Кулона - Амонтона (напряжение трения равно произведению коэффициента трения на нормальное давление). На этом участке касательные напряжения возрастают, пропорциональны нормальному напряжению и изменяются от (х =0,5∙а) до (х = хв = 0,5∙а - ψ∙h).
Изменение нормального напряжения описывается уравнением:
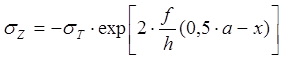
Изменение касательного контактного напряжения - уравнением:
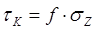
Однако увеличение абсолютной величины  с уменьшением х может происходить до значения
с уменьшением х может происходить до значения 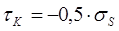 .
.
Эпюра нормальных напряжений в зоне скольжения – возрастающая показательная кривая. Эпюра касательных напряжений в зоне скольжения – возрастающая показательная кривая.
|
|
|
Вариант 1
Крайние значения:
При х = 0,5∙140 = 70 мм:
 МПа.
МПа.
 МПа.
МПа.
При х = хв = 0,5∙140 – 0,28∙22 = 63,84 мм:
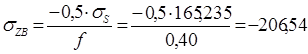 МПа.
МПа.
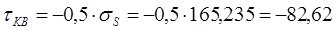 МПа.
МПа.
Промежуточные значения:
При х = 68 мм:
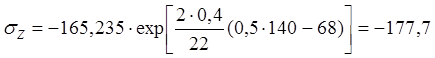 МПа.
МПа.
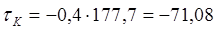 МПа.
МПа.
При х = 66 мм:
 МПа.
МПа.
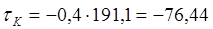 МПа.
МПа.
Зона торможения – участок от (х = хв) до (х = хс = h), в котором равновероятно скольжение металла по инструменту и сдвиги внутри металла по плоскостям, параллельным контактной плоскости. После того как 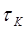 достигнет значения
достигнет значения 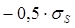 , а
, а  значения
значения  , рост касательного напряжения
, рост касательного напряжения 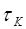 прекращается и оно принимает постоянное значение
прекращается и оно принимает постоянное значение  постоянства касательных напряжений
постоянства касательных напряжений
Изменение нормального напряжения описывается уравнением:
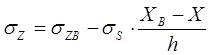
Изменение касательного контактного напряжения - уравнением:
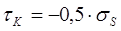
Эпюра нормальных напряжений в зоне торможения – возрастающая прямая (линейная зависимость). Эпюра касательных напряжений в зоне торможения – горизонтальная прямая (неизменная величина).
Крайние значения:
При х = хв = 63,84 мм:
 МПа (см.выше)
МПа (см.выше)
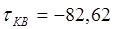 МПа.(см.выше)
МПа.(см.выше)
При х = хс ≈ h ≈ 22 мм:
 МПа.
МПа.
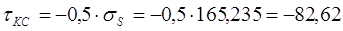 МПа.
МПа.
Зона прилипания – участок, где контактные касательные напряжения меняют своё направление при переходе через середину полосы и на контактной поверхности изменяются по линейному закону. Возрастание нормальных напряжений происходит менее интенсивно, чем в предыдущих зонах. Величина нормального напряжения на оси полосы имеет максимальное значение. Экспериментально установлено, что за границу этой зоны можно приближённо принять абсциссу, равную толщине образца, т.е. от (х = хс ≈ h) до (х = х0 = 0)
Изменение нормального напряжения описывается уравнением:
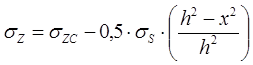
Изменение касательного контактного напряжения - уравнением:

Эпюра нормальных напряжений в зоне прилипания – параболическая зависимость. Эпюра касательных напряжений в зоне прилипания – наклонная прямая, проходящая через начало координат (линейная зависимость).
|
|
|
Крайние значения:
При х = хс ≈ 22 мм:
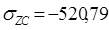 МПа (см.выше)
МПа (см.выше)
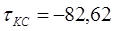 МПа.(см.выше)
МПа.(см.выше)
При х = х0 = 0 мм:
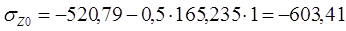 МПа.
МПа.
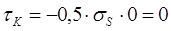 МПа.
МПа.
Промежуточные значения:
При х = 20 мм:
 МПа.
МПа.
При х = 15 мм:
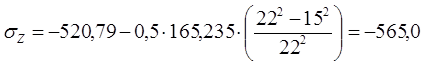 МПа.
МПа.
При х = 10 мм:
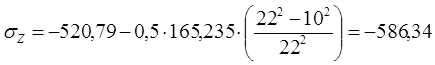 МПа.
МПа.
При х = 5 мм:
 МПа.
МПа.
Протяжённость участков зависит от соотношения ширины полосы к её толщине и от величины коэффициента трения.

Рисунок 7.Эпюра распределения контактных нормальных напряжений

Рисунок 8. Эпюра распределения контактных касательных напряжений
|
|
|


