 |
Лабораторная работа №4. Опытная проверка уравнения бернулли при преобразовании пьезометрического и динамического давления
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №4
ОПЫТНАЯ ПРОВЕРКА УРАВНЕНИЯ БЕРНУЛЛИ ПРИ ПРЕОБРАЗОВАНИИ ПЬЕЗОМЕТРИЧЕСКОГО И ДИНАМИЧЕСКОГО ДАВЛЕНИЯ
Цель работы: опытно изучить преобразование динамического давления в пьезометрическое и наоборот.
Работу проводить на участках 10 – 11 (диффузор) и 12 – 13 (конфузор) в воздухопровода (см. рис. 9).
Схема конфузора и эпюра давлений показаны на рис. 13.
По уравнению Бернулли 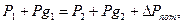
по формуле (9)
 - потерянное давление,
- потерянное давление, 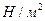 (мм. в. ст. );
(мм. в. ст. );
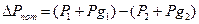 (24)
(24)
На рис. 14 показана схема диффузора и эпюра давлений.
Здесь 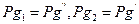
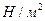 (мм. в. ст. );
(мм. в. ст. );
 определить по формуле (24).
определить по формуле (24).
Порядок проведения работы
1. Опыты проводить на трех расходах воздуха.
2. Перед началом работы выполнить замеры для определения плотности и расхода воздуха.
Результаты занести в табл. 4. 1.
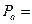
 (мм. рт. ст. );
(мм. рт. ст. );
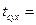
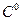 - температура сухого термометра;
- температура сухого термометра;
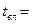
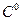 - температура влажного термометра;
- температура влажного термометра;
Таблица 4. 1
| №
| По результатам замеров | По результатам расчетов | |||||||||||
| 
| 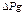
| 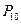
| 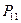
| 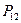
| 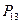
| 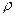
| 
| 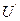
| 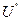
| 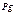
| 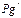
| |
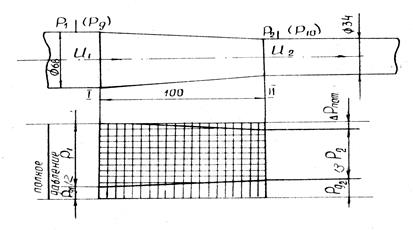
Рисунок 13. Схема конфузора и эпюра давлений
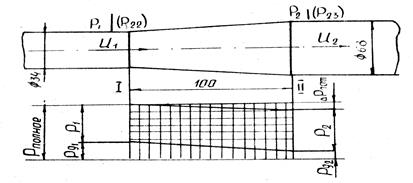
Рисунок 14. Схема диффузора и эпюра давлений
По результатам замеров следует произвести расчеты в следующем порядке:
1. Плотность воздуха 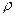 у измерительной диафрагмы по формуле (3) или (4).
у измерительной диафрагмы по формуле (3) или (4).
2. Расход воздуха V по формуле (5).
3. Средние скорости воздуха в воздухопроводе 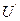 и
и 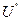 по формулам (7) и (8).
по формулам (7) и (8).
4. Динамические давления 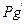 и
и 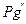 по формуле (9).
по формуле (9).
Результаты этих расчетов занести в табл. 4. 1.
|
|
|
Дальнейшие расчеты занести в табл. 4. 2.
Таблица 4. 2
| № | Конфузор | Диффузор | |||||||||||
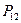
| 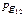
| 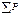
| 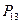
| 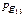
| 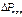
| 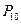
| 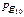
| 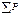
| 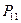
| 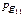
| 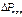
| 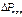 расч.
расч.
| |
5. Потерянное давление  по формуле (24).
по формуле (24).
6. По результатам замеров и расчетов под эскизами конфузора и диффузора в масштабе построить эпюры давлений для каждого опыта отдельно (по 3 эпюры).
7. Кроме того, для диффузора необходимо определить потерю давления расчетным путем
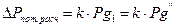 ,
,
где 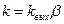 - коэффициент потери давления в диффузоре;
- коэффициент потери давления в диффузоре;
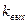 - по графику рис. 10.
- по графику рис. 10.
Поправочный коэффициент 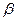 определить по графику рис. 15 в зависимости от угла раскрытия диффузора.
определить по графику рис. 15 в зависимости от угла раскрытия диффузора.
Угол раскрытия диффузора можно определить по формуле (25)
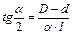 , (25)
, (25)

Полученные результаты  сравнить с опытными.
сравнить с опытными.
Контрольные вопросы
1. Что такое конфузор?
2. Что такое диффузор?
3. Назначение конфузора и диффузора.
ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ:
1. Приступать к выполнению лабораторной работы только с разрешения преподавателя.
2. При обращении со стеклянными приборами соблюдать осторожность и бережное обращение.
3. Запуск и остановку вентилятора производит лаборант по указанию
преподавателя или преподаватель.
4. Не загораживать выход воздуха из установки.
5. По окончании работы все переносные приборы сдаются преподавателю (лаборанту).
Рекомендуемая литература
1. Металлургическая теплотехника: В 2 т. Т. I. Теоретические основы: Учеб. для вузов / В. А. Кривандин, В. А. Арутюнов, Б. С. Мастрюков и др. – М.: Металлургия, 1986. – С. 88 – 94.
Казанцев Е. И. Промышленные печи: Справочник. – М.: Металлургия,
ЛАБОРАТОРНАЯ РАБОТА №5
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ ЧЕРЕЗ МНОГОСЛОЙНУЮ СТЕНКУ
|
|
|
Цель работы: Познакомиться с математическим и графическим методом определения теплопроводности материалов через многослойную стенку.
Общие сведения
В природе широко распространены процессы, связанные с переносом массы и энергии. Сюда относятся молекулярная и турбулентная диффузия, вязкость и теплопроводность.
Механизм передачи тепла теплопроводностью весьма сложен. Колебательные движения атомов в кристаллической решетке твердого вещества способствуют передачи тепла в теле. Кроме того, в металлах тепло переносится электронами проводимости, образующими " электронный газ" или электронную плазму, пронизывающую кристаллическую решетку. Большая электропроводность тела сопровождается и высокой теплопроводностью.
Показателем способности проводить тепло является коэффициент теплопроводности 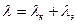 , который состоит из двух слагаемых:
, который состоит из двух слагаемых:
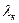 - проводимость, зависящая от колебательных движений атомов в решетке, и
- проводимость, зависящая от колебательных движений атомов в решетке, и 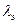 - проводимость, обязанная обмену электронами. Опыт показывает, что у металлов
- проводимость, обязанная обмену электронами. Опыт показывает, что у металлов 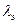 > >
> > 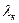 .
.
Пористая структура вещества усложняет процесс теплопроводности ещё более. Теплопроводность заменяется совместным действием различных видов теплопередачи. В порах тепло передаётся излучением от одной перегородки к другой. Перегородки являются экранами. Поры заняты газами, теплопроводность газов очень мала, конвекция в микропорах также незначительна. Это уменьшает теплопроводность материала. Все это сказывается на коэффициент теплопроводности 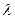 , который в этом случае уже не выражает собой чистую теплопроводность материалов, а представляет собой условную величину, эквивалентно заменяющую совместное действие теплопередачи различных видов внутри пористого тела.
, который в этом случае уже не выражает собой чистую теплопроводность материалов, а представляет собой условную величину, эквивалентно заменяющую совместное действие теплопередачи различных видов внутри пористого тела.
Тепло переходит в телах от более нагретой массы к менее нагретой. Разность температур является необходимым условием теплопередачи.
В случае одномерного потока теплопередача теплопроводностью может быть описана уравнением Фурье:
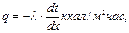
где q - удельный тепловой поток, который показывает, сколько больших калорий тепла передаётся через 1 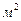 поперечного сечения тела в 1 час. Знак минус перед правой частью поставлен потому, что с увеличением значения х температурах t уменьшается, т. е. приращение температуры dt отрицательно.
поперечного сечения тела в 1 час. Знак минус перед правой частью поставлен потому, что с увеличением значения х температурах t уменьшается, т. е. приращение температуры dt отрицательно.
|
|
|
Величина 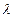 - коэффициент теплопроводности материала; он показывает, сколько тепла передаётся через 1
- коэффициент теплопроводности материала; он показывает, сколько тепла передаётся через 1  поперечного сечения тела в 1 час, когда длина проводника в направлении теплового потока равна 1 м и разность температур на концах тела равна 1°. Величина
поперечного сечения тела в 1 час, когда длина проводника в направлении теплового потока равна 1 м и разность температур на концах тела равна 1°. Величина 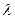 , зависит от технического состава, физической структуры, температуры материала проводника и др. Определяют
, зависит от технического состава, физической структуры, температуры материала проводника и др. Определяют 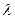 экспериментально или по эмпирическим формулам из справочника.
экспериментально или по эмпирическим формулам из справочника.
В твёрдых телах теплопроводность в зависимости от температуры изменяется по-разному. Теплопроводность материалов с плотной кристаллической структурой (без пор) по мере повышения температуры, как правило, уменьшается. К таким материалам можно отнести металлы и минералы с кристаллической структурой, например магнезит.
Теплопроводность пористых, аморфных или стекловидных материалов с повышением температуры увеличивается. Сюда относятся шамот, динас, красный кирпич, асбест и другие многопористые материалы. Повышение теплопроводности для материалов этой группы следует объяснить увеличением доли тепла, передаваемого излучением в порах.
Истинная зависимость теплопроводности 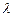 от температуры t достаточно сложна. Для решения технических задач в целях упрощения принимают линейную зависимость
от температуры t достаточно сложна. Для решения технических задач в целях упрощения принимают линейную зависимость 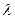 от t что достаточно хорошо совпадает с экспериментальными данными:
от t что достаточно хорошо совпадает с экспериментальными данными:
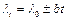
Поскольку температура по толщине слоя, через который проходит тепловой поток q, меняется, то используется 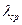 - средний коэффициент теплопроводности в интервале температур
- средний коэффициент теплопроводности в интервале температур 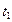 и
и 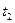 :
:
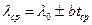
Величина 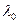 - коэффициент теплопроводности при
- коэффициент теплопроводности при 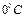 , который в огнеупорах весьма сильно изменяется, уменьшаясь с увеличением пористости тела. На рисунке 15 показано распределение температур через плоскую однослойную стенку.
, который в огнеупорах весьма сильно изменяется, уменьшаясь с увеличением пористости тела. На рисунке 15 показано распределение температур через плоскую однослойную стенку.
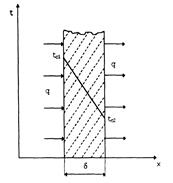
Рисунок 15. Распределение температур в плоской однослойной стенке
Количество тепла, проходящего через плоскую однородную стенку, определяется по формуле:
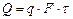
|
|
|
где q - плотность теплового потока, 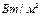 .
.
F - площадь стенки, 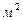
 - длительность нагрева, час.
- длительность нагрева, час.
Распределение температур по толщине однослойной стенки имеет линейную зависимость, т. е. описывается уравнением:
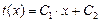 ;
;
где:
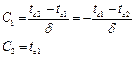
Тогда искомое распределение температур по толщине однослойной стенки будет иметь вид:
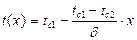 ; (1)
; (1)
Используя уравнение Фурье и продифференцировав уравнение (1) определяем плотность теплового потока, проходящего через стенку:
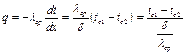
где 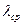 - средний коэффициент теплопроводности. Вт/(м °С);
- средний коэффициент теплопроводности. Вт/(м °С);
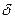 - толщина стенки, м;
- толщина стенки, м;
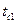 и
и 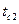 -температуры, поддерживаемые на поверхностях стенки, °С.
-температуры, поддерживаемые на поверхностях стенки, °С.
Отношение 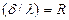 называют термическим сопротивлением стенки. Оно определяет падение температуры в стенке на единицу плотности теплового потока.
называют термическим сопротивлением стенки. Оно определяет падение температуры в стенке на единицу плотности теплового потока.
Стены металлургических печей и других нагревательных устройств обычно выкладывают из различных огнеупоров в несколько слоев: три, четыре, и более. Тогда для многослойной стенки, состоящей из n-слоёв. плотность теплового потока определяется по формуле:
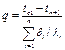 (2)
(2)
В знаменателе представлено общее термическое сопротивление стенки, как сумма частных термических сопротивлений каждого из слоев.
Так как в формуле (2) есть среднее значение коэффициентов теплопроводности для каждого из слоев, для их нахождения надо найти средние температуры каждого из слоев.
Внутри каждого слоя 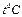 измеряется по прямой, но для многослойной стенки в целом она представляет собой ломаную линию. Значения неизвестных температур на границе слоев многослойной стенки можно уточнять графически. Так. например, для 3-х слойной стенки, при построении графика по оси абсцисс в произвольном масштабе, в порядке расположения слоев, откладываются значения их термических сопротивлений
измеряется по прямой, но для многослойной стенки в целом она представляет собой ломаную линию. Значения неизвестных температур на границе слоев многослойной стенки можно уточнять графически. Так. например, для 3-х слойной стенки, при построении графика по оси абсцисс в произвольном масштабе, в порядке расположения слоев, откладываются значения их термических сопротивлений 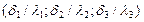 и восстанавливаются перпендикуляры. На крайних из восстановленных перпендикулярах также в произвольном, но в одинаковом масштабе, откладываются значения наружных температур
и восстанавливаются перпендикуляры. На крайних из восстановленных перпендикулярах также в произвольном, но в одинаковом масштабе, откладываются значения наружных температур 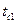 и
и 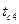 . Полученные точки А и С соединяются прямой Точки пересечения этой прямой со средними перпендикулярами дают значения искомых температур
. Полученные точки А и С соединяются прямой Точки пересечения этой прямой со средними перпендикулярами дают значения искомых температур 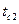 и
и  . На рисунке 16 представлен графический метод определения температур в 3 - х слойной стенке.
. На рисунке 16 представлен графический метод определения температур в 3 - х слойной стенке.
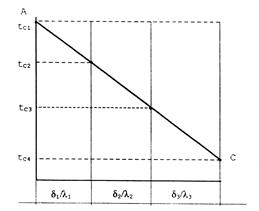
Рисунок 16. Графический способ определения промежуточных
температур
Приборы и материалы : муфельная печь, двухслойный образец из огнеупорных материалов (магнезита и шамота), термопара типа ХА, милливольтметр, термометр.
|
|
|
|
|
|


