Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

б) Сигнал со случайной начальной фазой




Распределение помехи релеевское, но при больших отношениях «сигнал-шум» распределение сводится к нормальному

qo=Ö-2×ln(Pлт).

Тогда для Pлт1=10-3, qo=3,72;

             Pлт2=10-5, qo=4,8.

Таблица 4.2

Точки построения кривой обнаружения для сигнала с неизвестной начальной фазой*

q P лт1 =10-3 P лт2 =10-5
1 0,00326 0,00007
2 0,4272 0,0025
3 0,2358 0,035
4 0,6103 0,21
5 0,8997 0,57
6 0,9887 0,88
7 0,99841 0,98
8 0,99999 0,9993
9   0,99999

В) сигнал со случайной фазой и амплитудой

qo=Ö-2×ln(Pлт).

Тогда для Pлт1=10-3, qo=3,72;

             Pлт2=10-5, qo=4,8.

Расчет точек для кривой обнаружения.

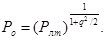
Таблица 4.3

Точки построения кривой обнаружения для сигнала с неизвестной начальной фазой и амплитудой*

q P лт1 =10-3 P лт2 =10-5
1 0,01 0,0005
2 0,1 0,02
3 0,2848 0,11
4 0,4642 0,28
5 0,5995 0,42
6 0,6852 0,55
7 0,7627 0,64
8 0,8111 0,7
9 0,8467 0,76
10 0,8753 0,8
11 0,8938 0,83
12 0,9097 0,85
13 0,9224 0,87
14 0,9326 0,89
15 0,941 0,91
16 0,9479 0,92
17 0,9536 0,924
18 0,9585 0,93
19 0,9627 0,944
20 0,9662 0,95

 

Расчет характеристик обнаружения

а) Находим энергию сигнала при Pomin=0,92

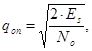 тогда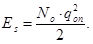

Данные наших расчетов приведены в приложении (рис.1) и (рис.2).

Таблица 3.4

Энергия сигнала при заданной минимальной вероятности правильного обнаружения

Сигнал

P лт1 =10-3

P лт2 =10-5
qn Es qn Es
полностью известный 4,5 2,261×10-13 6 3,015×10-13
со случайной начальной фазой 5,1 2,563×10-13 6,7 3,367×10-12
со случайной фазой и амплитудой 13 6,533×10-12 17 1,005×10-12

 

б) энергия минимального сигнала при когерентном и некогерентном приеме.

Еи=Es/n –для когерентного приема.

Еи=Es/Ön – для некогерентного приема.

n=1 и n=20 – число сигналов принимаемой последовательности.

Для n=1 различие между когерентным и некогерентным приемами отсутствуют.

Таблица 4.5

Энергия минимального порогового сигнала

   

P лт1 =10-3

P лт2 =10-5
сигнал вид приема n=1 n=20 n=1 n=20

точно известный

 когерент.

2,261×10-12

 1,508×10-14

3,015×10-13

 2,01×10-14
некогерент. 5,839×10-13 7,785×10-13

со случ. нач. фазой

 когерент.

2,563×10-13

 1,709×10-14

3,367×10-12

 2,245×10-14
некогерент. 6,617×10-13 8,694×10-13

со случ. нач. фазой и амп.

 когерент.

6,533×10-12

 4,355×10-14

1,005×10-12

 6,701×10-14
некогерент. 1,687×10-13 2,595×10-13

 

в) коэффициент распознавания

d=qоп/Ön – для когерентного приема.

d=qоп/4Ön – для когерентного приема.

Таблица 4.6

Коэффициент распознавания, d

   

P лт1 =10-3

P лт2 =10-5
сигнал вид приема n=1 n=20 n=1 n=20

точно известный сигнал

 когерент.

4,5

 1,162

6

 1,549
некогерент. 2,287 3,049

сигнал со случ. нач. фазой

 когерент.

5,1

 1,317

6,7

 1,73
некогерент. 2,591 3,404

сигнал со случ. нач. фазой и амп.

 когерент.

13

 3,357

17

 5,164
некогерент. 6,606 10,163

г) импульсная мощность

Wи=Es/tи, для n=1;

Wи=Eи/tи, для n=20.

Таблица 4.7

Импульсная мощность Wи, Вт

   

P лт1 =10-3

P лт2 =10-5
сигнал вид приема n=1 n=20 n=1 n=20

точно известный

 когерент.

3,354×10-10

 2,236×10-11

4,472×10-10

 2,981×10-11
некогерент. 8,659×10-11 1,155×10-11

со случ. нач. фазой

 когерент.

3,801×10-10

 2,534×10-11

4,993×10-10

 3,329×10-11
некогерент. 9,814×10-11 1,289×10-10

со случ. нач. фазой и амп.

 когерент.

9,688×10-10

 6,459×10-11

1,491×10-9

 9,937×10-10
некогерент. 2,502×10-10 3,849×10-10

 

ВЫВОД

 

 В данной курсовой работе были рассчитаны и построены кривые семейства характеристик обнаружения и определены значения порогового сигнала для исходных данных. Расчет проводился для когерентной последовательности и некогерентной последовательности импульсов при полностью известном сигнале, со случайной начальной фазой и амплитудой. По результатам расчетов видно что при некогерентном сигнале коэффициент распознавания выше, чем при когерентном, также при этом выше и импульсная мощность. Также можно сделать вывод, что у различных сигналов, таких, например, как полностью известный сигнал и сигнал со случайной начальной фазой, будут разные энергий при заданной минимальной вероятности правильного обнаружения, в первом случае она меньше.

 

ПРИЛОЖЕНИЕ

 

 

 


* см. приложение (рис.1 и рис.2)

* см. приложение (рис.1 и рис.2)

* см. приложение (рис.1 и рис.2)
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...