Главная | Обратная связь | Поможем написать вашу работу!

Общие сведения о методике тепловых расчетов рудничного воздуха

Процесс теплообмена является нестационарным и физическая модель его может быть представлена в общем виде следующим образом. В момент проведения горных выработок температура пород равна средней температуре горного массива на данной глубине. Эта температура определяется местом расположения шахты, геотермическим градиентом, глубиной залегания, характеристикой пород и другими факторами. В начальный момент величина тепловыделений определяется коэффициентом теплоотдачи α, зависящим, как известно, от числа Re, размеров и формы поперечного сечения и шероховатости стенок выработки. В начале процесса более интенсивно охлаждаются ближайшие к вентиляционной струе породные слои массива; при значительном удалении от поверхности охлаждения уменьшение температуры становится малозаметным. С течением времени, по мере охлаждения поверхностных слоев, увеличивается также и степень охлаждения пород на большей глубине.

Вследствие охлаждения поверхностных слоев возрастает их термическое сопротивление, ввиду чего происходит непрерывное уменьшение тепловыделений. Увеличение термического сопротивления переходу тепла от медленно охлаждающихся глубинных массивов через слои, имеющие во времени различную степень охлаждения (обратно пропорциональную их расстоянию от ограничивающей массив поверхности), приводит к тому, что распределение температур в массиве в каждый данный момент времени происходит по весьма сложным законам. Руководствуясь этой физической моделью, А.Ф. Воропаев, используя метод конечных разностей, установил качественное и количественное распределение нестационарных температур в околоствольных массивах при теплообмене стенок ствола с вентиляционной струей. При теоретическом решении задачи распределение температур определялось автором для бесконечного тела, ограниченного плоской поверхностью, с последующим приближенным переходом к цилиндрической форме ограничивающей поверхности. Такое упрощение процесса теплообмена между массивом и воздухом в точных решениях может быть допущено только для стволов угольных шахт из-за относительно незначительного влияния этого теплообмена (по сравнению с рудными шахтами, породы которых обладают значительно большей теплопроводностью) на изменение параметров воздуха в стволе. А.Ф. Воропаев предложил формулы для определения температуры воздуха в стволах глубоких угольных шахт с учетом влияния тепла горного массива и сезонных колебаний температуры атмосферного воздуха. Составляя дифференциальное уравнение теплового баланса элемента выработки, А.Ф. Воропаев принял упрощающее допущение, что тепло от окислительных процессов равно теплу, расходуемому на увлажнение воздуха.

Наиболее распространенными в практике тепловых расчетов угольных шахт являются формулы, предложенные академиком А.Н. Щербанем, которые получены решением дифференциального уравнения теплопроводности полого горного массива, ограниченного цилиндрической поверхностью, при заданном законе ее теплообмена с воздухом и температуре, постоянной во времени. Положительным здесь является то, что решение уравнения произведено методом операционного исчисления, который наиболее подходит к решению такого рода задач (теплопередача цилиндрических тел). Анализ исходного уравнения позволил автору исследовать характер образования и роль в процессе теплообмена сезонных и суточных теплоуравнивающих оболочек. Из анализа этих решений, произведенного О.А. Кремневым, следует, что они больше приближаются к точным решениям для периода проветривания выработок от года до 10 лет.

Как показали исследования Ю.Д. Дядькина, график изменения температуры воздуха в выработке описывается выпуклой кривой, так как вследствие увеличения температуры воздуха и уменьшения напора теплоотдача пород по длине выработки уменьшается.

О.А. Кремнев предложил точное аналитическое решение задачи нестационарной теплопроводности бесконечных полых однородных цилиндров и дал критериальную зависимость, которая упрощает использование довольно сложных формул.

Наиболее ценны теоретические исследования О.А. Кремнева в области процессов теплообмена в очистных и подготовительных забоях.

Для прямых и обратных тепловых расчетов он предложил отдельные формулы для вертикальных стволов, горизонтальных и наклонных выработок и очистных забоев. Погрешности, получаемые при расчетах (несколько завышенные значения температур при обратных расчетах и заниженные - при прямых), обуславливаются тем, что автор принимает прямолинейный закон изменения влагосодержания воздуха независимо от характера изменения температуры в пределах расчетного участка.

В одной из последних работ Ю.Д. Дядькина подвергнуты всестороннему анализу существующие методы тепловых расчетов шахт и предложены формулы, которые получены из правильной физической модели нестационарного теплообмена в протяженных горных выработках и очистных забоях. Недостатком этих формул является то, что они не учитывают сезонных колебаний температуры атмосферного воздуха, которые по наблюдениям, проведенным ДГИ на металлических рудниках, оказывают существенное влияние на атмосферные условия в горных выработках.

Как указывает А.Н. Щербань, расчетная формула Ю.Д. Дядькина неприменима для горизонтальных и наклонных выработок средней и большей протяженности, так как автором принят прямолинейный закон изменения влагосодержания воздуха при постоянстве его относительной влажности по длине выработки, что не соответствует действительности.

Из приведенного обзора следует, что подавляющее большинство исследователей проводили изучение атмосферных тепловых условий и теоретические исследования вопросов теплообмена в горных выработках применительно к горнотехническим условиям глубоких угольных шахт.

Примечания

1. Параметр из формулы находится следующим образом:

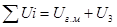
где - температура закладки, град;

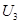-часть периметра соприкасающаяся с закладкой, м;

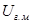- часть периметра соприкасающаяся с горным массивом, м;

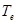- естественная температура породы, град.

. Коэффициент нестационарного теплообмена k_τнаходится из формулы

где Кu - критерий Кирпичева определяется по номограмме;

R₀ - эквивалентный радиус выработки, м;

λ_П - коэффициент теплопроводности пород на расчетном участке, Вт/ (м∙град).

. Эквивалентный радиус выработки R₀ находится по формуле

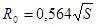
где S - площадь сечения выработки, м².

4. Критерий Био определяется по зависимости

где α - коэффициент теплоотдачи, Вт/ (м²∙⁰С).

. Коэффициент теплоотдачи находится по формуле

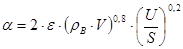
где ε - коэффициент шероховатости стенок выработки;

V - скорость воздуха, м/с;

ρ_В - плотность воздуха, кг/м³.

. Критерий Фурье находится по формуле

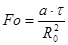
где а - температуропроводность горных пород на расчетном участке, м²/час;

τ - время проветривания расчетного участка, час.

Расчетная часть

4.1 Произведем расчет параметра :

Произведем расчет параметра α: \

V	0,179	0,268	0,538
α	2,23	3,07	5,29

Произведем расчет параметра Fo:

Произведем расчет параметра Bi:

Произведем расчет параметра k_τ:

при Ки=1,1 и при Ки=1,4 соответственно

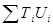Произведем расчет параметра :

=10+20=30

Влияние Q на температуру воздуха в забое:

Q; м³/с	t₂ при Q=10	t₂ при Q=15	t₂ при Q=30
N₁L₁ T₁∆φ₁	26,031	24,226	22,576
N₂L₂ T₂∆φ₂	28,391	25,874	23,576
N₃L₃ T₃∆φ₃	30,621	27,390	24,462

Влияние N на температуру воздуха в забое:

N; кВт	t₂ при N=100	t₂ при N=150	t₂ при N=400
L₁ Q₁T₁∆φ₁	26,031	26, 200	28,384
L₂ Q₂T₂∆φ₂	25,478	25,874	27,061
L₃ Q₃T₃∆φ₃	23,894	24,121	24,804

4.10 Влияние L на температуру воздуха в забое:

L; м	t₂ при L=100	t₂ при L=200	t₂ при L=300
N₁Q₁T₁∆φ₁	26,031	27,279	28,153
N₂ Q₂T₂∆φ₂	24,916	25,874	26,545
N₃ Q₃T₃∆φ₃	23,759	24,374	24,804

4.11 Влияние T на температуру воздуха в забое:

T; ⁰С	t₂ при T =24	t₂ при T =30	t₂ при T=36
N₁L₁ Q₁∆φ₁	26,031	26,674	27,278
N₂L₂ Q₂∆φ₂	25,328	25,874	26,391
N₃L₃ Q₃∆φ₃	24,102	24,462	24,804

4.12 Влияние ∆φ на температуру воздуха в забое:

∆φ;	t₂ при ∆φ=0,01	t₂ при ∆φ=0,03	t₂ при ∆φ=0,06
N₁L₁ T₁ Q₁	26,031	25,835	25,537
N₂L₂ T₂Q₂	26,075	25,876	25,576
N₃L₃ T₂Q₃	25, 195	25,048	24,804

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: