 |
Кривая нормального распределения и ее свойства
|
|
|
|
В результате многочисленных экспериментов было установлено, что при механической обработке деталей вероятность получения линейного размера в пределах некоторого интервала его изменения  определяется следующим выражением
определяется следующим выражением
 . (13.13)
. (13.13)
Функция
 (13.14)
(13.14)
называется плотностью вероятности случайных величин и выражает закон нормального распределения. График этой функции приведен на рис.13.2 и называется кривой нормального распределения.
Из формулы (13.14) следует, что плотность вероятности случайных величин для линейных размеров имеет размерность обратную длине, т.к. среднее квадратическое отклонение имеет данную размерность. В этой связи плотность вероятности следует рассматривать, как вероятность появления случайной величины в окрестности некоторой точки на отрезке единичной длины. В окрестностях  плотность вероятности высокая, т.е. вероятность появления случайной величины в окрестностях этой точки максимальная. С увеличением разности
плотность вероятности высокая, т.е. вероятность появления случайной величины в окрестностях этой точки максимальная. С увеличением разности  плотность распределения уменьшается.
плотность распределения уменьшается.
Геометрически  представляет собой площадь фигуры на отрезке
представляет собой площадь фигуры на отрезке  под кривой нормального распределения.
под кривой нормального распределения.
Для достаточно узкого интервала согласно теореме о среднем
 ;
;  . (13.15)
. (13.15)
Кривая нормального распределения имеет следующие свойства:
1. Ось  является асимптотой для ее ветвей.
является асимптотой для ее ветвей.
2. При 
 . (13.16)
. (13.16)
3. Кривая имеет две точки перегиба  и
и  , которые находятся на расстоянии
, которые находятся на расстоянии  от оси симметрии (рис.13.2). Ординаты их равны
от оси симметрии (рис.13.2). Ординаты их равны
 . (13.17)
. (13.17)
4. Если случайная величина подчиняется нормальному закону распределения и может принимать любые численные значения в интервале  , то
, то
 . (13.18)
. (13.18)
Это свойство вытекает из положения, что вероятность появления случайной величины в интервале  равна единице.
равна единице.
|
|
|
Положение кривой относительно начала координат, и ее форма определяются двумя параметрами  и
и  . С изменением
. С изменением  форма кривой остается прежней. Изменяется ее положение относительно начала координат (рис. 13.3). С изменением
форма кривой остается прежней. Изменяется ее положение относительно начала координат (рис. 13.3). С изменением  центр кривой остается на прежнем месте. Изменяется ее форма (рис.13.4). С увеличением
центр кривой остается на прежнем месте. Изменяется ее форма (рис.13.4). С увеличением  кривая растягивается и уменьшается по высоте. Таким образом,
кривая растягивается и уменьшается по высоте. Таким образом,  является мерой рассеяния случайной величины.
является мерой рассеяния случайной величины.
Нормирование распределения, функция Лапласа
Введем новую переменную  . После замены переменной в (13.13) получаем
. После замены переменной в (13.13) получаем
 (13.19)
(13.19)
где  и
и  - новые пределы интегрирования.
- новые пределы интегрирования.
Это действие называется нормированием распределения.  . После нормирования плотность вероятности выразится следующим образом
. После нормирования плотность вероятности выразится следующим образом
 (13.20)
(13.20)
Сущность операции нормирования заключается в сведении всего многообразия кривых распределения к одной, зависящей только от нормированной переменной. Для этой кривой среднее арифметическое равно нулю, а среднее квадратическое отклонение равно единице. Графическая интерпретация процедуры нормирования заключается в совмещении центра группирования с началом новой системы координат  . В этом случае кривая нормального распределения становится симметричной относительно оси ординат и называется плотностью вероятности нормированного распределения.
. В этом случае кривая нормального распределения становится симметричной относительно оси ординат и называется плотностью вероятности нормированного распределения.
Пусть  ;
;  . Тогда
. Тогда
 , (13.21)
, (13.21)
Интеграл  называется функцией Лапласа.
называется функцией Лапласа.
Геометрически функция Лапласа выражает площадь фигуры под кривой плотности вероятности нормированного распределения  в промежутке от 0 до
в промежутке от 0 до  . Интеграл в
. Интеграл в  нельзя выразить в элементарных функциях и его значение задано в специальных таблицах.
нельзя выразить в элементарных функциях и его значение задано в специальных таблицах.
Применение функции Лапласа позволяет вычислить теоретические частость и частоту. Из выражений (13.13) и (13.14) полагая  получаем
получаем
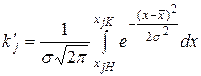 . (13.22)
. (13.22)
Выполним операцию нормирования. В результате замены переменной будем иметь

 , (13.23)
, (13.23)
где  и
и  - новые пределы интегрирования.
- новые пределы интегрирования.
|
|
|
Тогда
 (13.24)
(13.24)
|
|
|


