 |
Локальная и нелокальная задачи для уравнения смешанного типа второго порядка с оператором Геллестедта
|
|
|
|
Соиск. Дзарахохов А.В.
Кафедра математики.
Горский государственный аграрный университет
Доказана однозначная разрешимость локальной и нелокальной краевых задач для нагруженных уравнений 2 порядка оператора Геллестедта.
Рассмотрим уравнение
(1)
в области Ω, ограниченной отрезками АА0, ВВ0, А0В0 прямых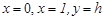 
соответственно и характеристиками
уравнения (1) в полуплоскости y<0, λ(y) – заданная непрерывная функция.
Пусть 
– параболическая, 
- гиперболическая области Ω, 
- интервал прямой y=0.
ЗАДАЧА 1. Найти в областях Ω1, Ω2 решение
уравнения (1), удовлетворяющее краевым условиям
, (2)
, (3)
где 
- непрерывные, а 
- дважды непрерывно дифференцируемая функции, причем
. (4)
Решение задачи Коши 
для уравнения (1), y<0, в области Ω2 имеет вид [1]:
, (5)
где 
.
Удовлетворяя (5) заданному условию (3), получим
. (6)
В равенстве (6) сделаем замену
.
В результате получим
.
Заменяя в последнем равенстве x через 
, получаем:
. (7)
Из равенства (7) находим
, (8)
где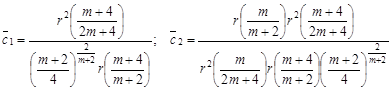 
.
Обращая (8) как обобщенное интегральное уравнение Абеля относительно 
, получаем [2]:
. (9)
Или с учетом перестановки Дирихле порядка интегрирования во втором интеграле правой части (9), получаем:
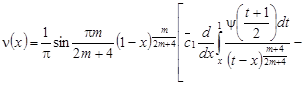
. (10)
Рассмотрим
.
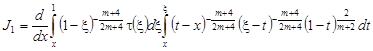Произведя замену переменных 
в последнем равенстве, получим
. На основании равенства [3]
будем иметь
. (11)
Подставляя (11) в (10), окончательно получаем функциональное соотношение между 
и 
, привнесенное из гиперболической части области Ω на линию y = 0:
. (12)
При m = 0 оно принимает вид:
. (13)
Устремляя 
из Ω1, получаем функциональное соотношение между и , привносимое на линию y = 0 в виде:
. (14)
В начале рассмотрим случай, когда m = 0. Исключая из уравнения (13) и (14) и, учитывая краевые условия (2), приходим к задаче
|
|
|
, (15)
. (16)
Решение (15), (16) представим в виде:
, (17)
где обозначено
.
Отсюда полагая x=x0, в силу условия (14) однозначно найдем 
. Затем подставляя это значение в (17) полностью определяем 
.
После определения в области Ω1 приходим к задаче (1), (2) и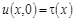 
. Нетрудно убедиться, что решение 
этой задачи удовлетворяет интегральному уравнению
, (18)
где 
– функция Грина указанной выше смешанной задачи для уравнения теплопроводности. Отсюда, полагая в (18) x = x0, для функции 
получаем интегральное уравнение
(19)
с ядром
и правой частью 
.
Уравнение (19) является интегральным уравнением Вольтерра второго рода и оно безусловно разрешимо в пространстве 
.
ЗАДАЧА 2. Требуется найти функцию 
, удовлетворяющую всем условиям задачи 1, кроме второго условия из (2) и (4), вместо которых берут условия:
, (20)
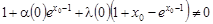. (21)
Для решения задачи 2, поступая как выше, с учетом условия (21) функцию однозначно определим решением уравнения (15), удовлетворяющим условиям
.
Пользуясь функцией Грина 
второй краевой задачи для уравнения теплопроводности, убеждаемся, что решение 
задачи 2 в области Ω1 удовлетворяет уравнению
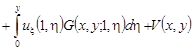, (22)
где 
.
Отсюда полагая в (22) x = x0 и учитывая условие (20), получаем систему интегральных уравнений Вольтерра второго рода относительно 
и 
:
(23)
,
,
,
.
В силу свойства функции Грина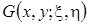 
и ядер системы (23), нетрудно убедиться, что система уравнений (23) допускает единственное решение в пространстве 
[4].
Пусть теперь m > 0. Исключая 
из системы уравнений (12) и (15), получаем интегродифференциальное уравнение относительно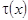 
:
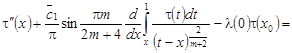
, (24)
удовлетворяющее граничному условию
(25)
в случае задачи 1 и нелокальному условию
(26)
в случае задачи 2.
Интегрируя равенство (24) дважды от 0 до x, с учетом граничных условий (25), (26), получаем:
(27)
Преобразуем двойной интеграл в левой части равенства (27):
|
|
|
. (28)
Учитывая равенство (28) в (27), получаем:
(29)
где 
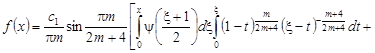
. (30)
Преобразуем двойные интегралы в равенстве (30). В результате получим
,
.
Учитывая J3 и J4 в равенстве (30), окончательно будем иметь:
Откуда заключаем, что 
. Таким образом, относительно 
получим интегральное уравнение Фредгольма второго рода:
, (31)
|
.
Так как 
, то обращая (31) через резольвенту R(x, t), будем иметь
, (31)
где 
Полагая в равенстве (31) х=х0 и х=1, однозначно определим
,
, если выполнены условия
.
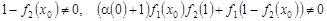После определения функции 
в области Ω1 приходим к задаче (1), (2) и 
, которая на основании свойств функции Грина эквивалентно редуцируется к интегральному уравнению Вольтерра второго рода. В области Ω2 решение задачи 2 задается формулой (5).
Список литературы
Бицадзе А.В. Уравнения смешанного типа. М.: ВИНИТИ АН СССР, 1959.
Трикоми Ф.О. О линейных уравнениях смешанного типа. М.: ОГИЗ, 1947.
Мюнтц Г. Интегральные уравнения //Л.-Н.ГТТИ. 1934. Т1.
Елеев В.А. Краевые задачи для нагруженного гиперболо-параболического уравнения с характеристической линией изменения типа // Украинский мат. журнал. Киев, 1995. Т.47, №12.
|
|
|
