Каковы законы распределения местных скоростей в живом сечении потока при ламинарном и турбулентном режимах

Негосударственное образовательное учреждение

Среднего профессионального образования

«Нефтяной техникум»

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ

«Гидравлика»

№ Варианта 7

Выполнил(а) студент(ка) заочного отделения 2 курса группы ИС14 Специальность:   Дата выполнения:	Дувакин Даниил Анатольевич «Сооружение и эксплуатация ГНП и ГНХ» «___»___________ 2016 г.
Проверил преподаватель: Королёва М.Р. В результате рецензирования получил оценку: __________, имеются замечания:___________________________ ________________________________________________________________________________________________________________________________________________
	Контрольную работу принял(а) _______________________________ Дата принятия: «___»_______2016 г. Рег. №_________________________

Ижевск

Г.

Содержание.

1)Каковы законы распределения местных скоростей в живом сечении потока при ламинарном и турбулентном режимах……………………………………………….3

2) Что называется вязкостью жидкости и от чего она зависит…………………….11

3)Задача №1……………………………………………………………………………13

4)Задача №2……………………………………………………………………………14

5)Задача №3……………………………………………………………………………15

6)Задача №4……………………………………………………………………………16

7)Задача №5……………………………………………………………………………17

8)Задача №6……………………………………………………………………………18

9)Список литературы...............................................................................................19

 

 

Каковы законы распределения местных скоростей в живом сечении потока при ламинарном и турбулентном режимах

Рассмотрим характер распределения скоростей в сечении потока при ламинарном и турбулентном режимах движения жидкости. Как показали теоретический анализ и опыты при ламинарном режиме движения жидкости в круглой трубе, скорости в поперечном сечении распределены по параболе (рис. 28), скорости у стенок трубы равны нулю и, плавно увеличиваясь, достигают максимума на оси потока.

При ламинарном режиме движения существуют лишь продольные составляющие скоростей. В этом случае силы сопротивления движению возникают вследствие трения между слоями жидкости, т. е. зависят от вязкости жидкости и не зависят (почти) от состояния стенок.

При турбулентном режиме закон распределения скоростей по живому сечению более сложен; в большей части сечения скорости близки к средней и резко падают в тонком слое у стенок, доходя до нуля. График распределения скоростей по сечению близок к трапеции (рис. 29). Такое распределение скоростей вызывается турбулентным перемешиванием в результате поперечных перемещений частиц. Быстро движущиеся частицы жидкости из средней части потока сталкиваются с медленно движущимися частицами вблизи стенок, благодаря чему и происходит выравнивание скоростей.

И только в пограничном слое, где стенки препятствуют перемешиванию, скорость резко убывает. Экспериментально подтверждается, что при турбулентном режиме движении потери напора по длине зависят от состояния стенок, ограничивающих поток. Если пропускать по трубе жидкость с различными скоростями, начиная с ламинарного режима и постепенно переходя к турбулентному, и одновременно измерять потери напора, то можно получить график зависимости потерь напора от скорости 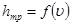(рис. 30). График показывает, что при скорости меньше некоторого предела потери напора прямо пропорциональны первой степени скорости (на графике участок 0-1).

Как и следовало ожидать, этот предел соответствует критической скорости

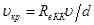(83)

После перехода от ламинарного режима к турбулентному потери напора растут пропорционально скорости в степени, большей единицы (на графике участок кривой 2-3). Переход от ламинарного режима к турбулентному может происходит и при числах Рейнольдса, больших критического.

Обратный же переход от турбулентного режима к ламинарному осуществляется при почти одинаковом значении , которое и считается критическим.

Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению

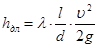, (84)

где l – длина участка трубы, м; d –внутренний диаметр трубопровода, м; v – средняя скорость потока, м/сек; g –ускорение свободного падения, м/сек2; 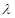– безразмерный коэффициент гидравлического трения.

Впервые формула (84) была получена эмпирическим путем в XIX в. и названа формулой Дарси-Вейсбаха. В дальнейшем указанная формула проверена теоретически на основе метода анализа размерностей.

В уравнении (84) остается не выясненным смысл безразмерного коэффициента 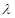. Для выяснения физического смысла коэффициента 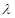при равномерном напорном движении жидкости в трубах как при ламинарном, так и при турбулентном режимах движения используем уравнение Д. Бернулли. Помня, что при равномерном напорном движении средняя скорость и распределение истинных скоростей по сечениям должны быть неизменными по длине трубопровода и составляя уравнение Д. Бернулли для двух сечений, можем записать

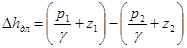. (85)

При горизонтальном расположении трубы и тогда

. (86)

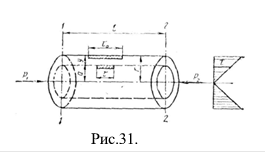
Для уточнения вопроса о потерях напора выделим в трубопроводе между сечениями 1-1 и 2-2 соосный цилиндр с радиусом а и длиной l (рис. 31).

Как оговорено выше, распределение скоростей в сечениях 1-1 и 2-2 одинаково, частицы жидкости двигаются без ускорений.

Напишем уравнение динамического равновесия рассматриваемого цилиндра

,

где –касательное напряжение (трения) на поверхности цилиндра.

Поделив обе части уравнения на 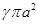, получим

.

Подставляя из уравнения (86) значение ,имеем

, (87)

или

. (88)

Выразим из уравнения (88)

(89)

(так как ).

У стенки трубы, где , значение равно

(90)

и тогда

. (91)

Уравнение (91) есть общее выражение потерь напора при равномерном движении жидкости в трубах. Подставляя в уравнение (91) значения , и , получим

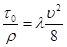. (92)

Замечаем, что имеет размерность квадрата скорости.

Обозначим

, (93)

где –называется скоростью касательного напряжения на стенке, или динамической скоростью. Тогда уравнение (92) примет вид

. (94)

Из уравнения (94) находим, что

. (95)

Таким образом, коэффициент гидравлического трения 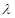прямо пропорционален отношению квадратов динамической и средней скоростей.

Потери напора при ламинарном движении. На основе изложенного выше для потерь напора по длине при ламинарном режиме движения жидкости в трубе получено следующее уравнение:

, (96)

где –абсолютный коэффициент вязкости жидкости, ; – длина трубопровода, м; v – средняя скорость, м/сек; – удельный вес жидкости, кгс/м3; 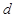– диаметр трубопровода, м.

Так как , а ,то вместо формулы (96) получим

.

Выражение называют формулой Пуазейля-Гагена (по имени ученых, получивших это уравнение).

Формула, что при ламинарном режиме потери напора пропорциональны средней скорости и не зависят от состояния стенок трубопровода.

Приравняв правые части уравнения Дарси-Вейсбаха и выражения, получим

.

Таким образом, коэффициент гидравлического трения при ламинарном режиме обратно пропорционален числу Рейнольдса.

Потери напора при турбулентном движении. В инженерной практике чаще встречается турбулентный режим движения жидкости в трубах, которые труднее исследовать теоретически. Этот вопрос подвергся наиболее широким опытным исследованиям как со стороны советских, так и зарубежных ученых. Из-за сложности процессов, протекающих при турбулентном режиме, до сих пор не создано окончательной теории, которая бы вытекала из основных уравнений гидродинамики и согласовывалась с опытом. Напомним, что при турбулентном режиме наблюдается интенсивное вихреобразование, частицы жидкости описывают сложные траектории, местные скорости меняются во времени даже при постоянном расходе. Это явление называется пульсацией скорости. Часть кинетической энергии жидкости переходит в тепловую. Установившегося движения в строгом смысле нет. Поэтому введено понятие об осредненной скорости.

Мгновенные скорости пульсируют около своего осредненного значения, которое за достаточно длительный промежуток времени остается постоянным; это значение и называется осредненной скоростью. В дальнейшем, говоря о скоростях, рассматривая турбулентное движение, будем подразумевать осредненные скорости.

Опытами установлено, что закон распределения осредненных скоростей по сечению и потери напора зависят от диаметра труб, средней скорости, вязкости жидкости и шероховатости стенок труб. В свою очередь характер шероховатости зависит от материала стенок труб, степени обработки, а последние определяют высоту выступов, их густоту и форму. Для приближенной оценки введено понятие средней высоты бугорков (выступов) шероховатости, называемой абсолютной шероховатостью и обозначаемой k. Очевидно, что чем меньше диаметр, тем быстрее частицы жидкости совершат пробег от центра трубопровода к стенкам и встретятся с бугорками шероховатости, и, отражаясь от них, вызовут возмущения в потоке жидкости. Следовательно, частота вихреобразования при малых диаметрах труб больше, и шероховатость той же высоты проявляется сильнее. Поэтому введено понятие относительной шероховатости, т. е. отношение абсолютной шероховатости к диаметру трубы .

Экспериментами установлено, что коэффициент гидравлического трения 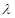в формуле Дарси-Вейсбаха, а соответственно и потери напора по длине зависят от числа Рейнольдса и от относительной шероховатости. Это вытекает и из теоретических исследований. Поэтому усилия как советских, так и зарубежных ученых были направлены на выявление характера этой зависимости. Было установлено, что при больших числах Рейнольдса и высокой шероховатости коэффициент гидравлического трения 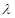в трубах совсем не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости (в этих условиях трубы и русла называют вполне шероховатыми). Трубы же, в которых коэффициент 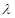зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Re и k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых 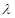зависит и от числа Рейнольдса и от относительной шероховатости, называются переходной областью. Это объясняется тем, что при малых числах Рейнольдса вблизи стенок сохраняется сравнительно толстый ламинарный слой, и выступы шероховатости обтекаются жидкостью без образования и отрыва вихрей. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление, и зависимость выражается в логарифмических координатах прямой (см. рис. 30).

С увеличением числа Рейнольдса ламинарный слой становится тоньше и не покрывает выступов шероховатости; при этом от выступов шероховатости начинают отрываться вихри, и свойства поверхности оказывают влияние на сопротивление движению; график зависимости отклоняется от прямой и переходит в кривую второго порядка.

Так как на характер сопротивлений оказывает влияние не только относительная шероховатость, но и форма и распределение выступов по поверхности, то в практику расчетов было введено понятие об эквивалентной равнозернистой шероховатости kэ. Под ней понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает при подсчетах одинаковое с заданной шероховатостью значение коэффициента гидравлического трения .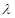

 

Что называется вязкостью жидкости и от чего она зависит В жидкостях наблюдаются явления переноса: диффузия, теплопроводность и вязкость. Вязкость жидкости – это перенос импульса от слоя к слою, текущей, например, по трубе жидкости (рис. 1.1). При течении жидкости по трубе различные слои имеют разные скорости. Наибольшая скорость течения у центрального слоя. Слой, прилегающий к стенкам трубы, покоится. Поэтому в направлении оси Х, перпендикулярной к направлению течения, возникает градиент скорости . Перенос импульса от слоя к слою осуществляется молекулами, изредка совершающими скачкообразные поступательные движения, меняя при этом положение равновесия, около которых они совершают колебания. При не очень высоких температурах такие перескоки происходят сравнительно редко. Перенос импульса вызывает изменение скорости движения слоев, то есть начинает действовать сила, которая по закону Ньютона равна , (1.1)

где F – сила внутреннего трения (вязкости) между слоями жидкости; 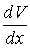– градиент скорости, характеризующий быстроту изменения скорости вдоль оси х, перпендикулярной к скорости; S – площадь поверхности, разделяющая два соседних слоя жидкости; h – коэффициент вязкости или коэффициент внутреннего трения.

Его физический смысл заключается в том, что она численно равен силе внутреннего трения, действующей на единичную площадь соприкасающихся слоев при градиенте скорости этих слоев равном единице. Размерность коэффициента вязкости в системе «СИ»:

 

 

Характерным для жидкости является сильная зависимость коэффициента вязкости от температуры. С повышением температуры вязкости жидкости быстро падает. При обычных давлениях коэффициент вязкости почти не зависит от давления. При давлении в тысячи и десятки тысячи атмосфер коэффициент вязкости быстро возрастает с ростом давления. Это объясняется тем, что в сильно сжатых жидкостях скачкообразные поступательные движения молекул становятся все более затруднительными. Молекулам все реже удается перескочить в другое место, так что обмен импульсом между слоями жидкости уменьшается. Коэффициент вязкости зависит от природы жидкости. Например, у бензина коэффициент вязкости ; у глицерина – .

 

 

Список литературы

1.Рабинович Е. 3. Гидравлика. — М.: Недра, 1978.

2.Рабинович Е. 3., Евгеньев А. Е. Гидравлика. — М.: Недра, 1978.

3.Цыбин Л. А., Шанаев И. А. Гидравлика и насосы. — М.: Недра, 1976.

4.Гулак И. А. Задачи по гидравлике. — М.: Недра, 1972.

 

Поделиться:

Воспользуйтесь поиском по сайту: