Задания и краткие методические указания к их выполнению по гидродинамике

Задание 1.1

При гидравлическом испытании участка трубопровода с внутренним диаметром d и длиной l, проводимом с целью обеспечения безопасности технологических процессов и недопущения загрязнения окружающей среды, манометрическое давление жидкости было поднято до значения 55 ат. Пренебрегая деформацией трубопровода и изменением температуры, определить какой объём жидкости вытек из негерметичного трубопровода, если через один час давление в нём упало до 40 ат. Модуль упругости жидкости принять равным 2,0 ×10⁹ Па.

Исходные данные для задания 1.1:

№ варианта	Параметр
d, м	l, м
	0,20

Краткие указания: В этой задаче необходимо учитывать сжимаемость (изменение объёма) капельной жидкости под воздействием давления. Сжимаемость характеризуется модулем упругости жидкости или коэффициентом объёмного сжатия, являющимся величиной обратной модулю упругости. Сжимаемость зависит, в основном, от рода жидкости. Физический смысл коэффициента объёмного сжатия заключается в относительном изменении объёма капельной жидкости при изменении давления на единицу. Давление в одну техническую атмосферу 1ат = 1кГ/см² = 9,81 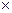10⁴ Па. Модуль упругости жидкости или коэффициент объёмного сжатия выбирается с использованием справочной литературы.

Вариант 4.

∆V = Vp – V0

P=a·ρ·v,

а- средняя скорость движения жидкости в трубопроводе до закрытия задвижки.

Скорость распространения ударной волны может быть вычислена по формуле:

,

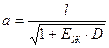где Е_ж - модуль упругости жидкости; d - внутренний диаметр трубы

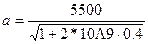= 0,06 м/с

 

55 ат = 539,55*10⁴ Па

40 ат = 392,4*10⁴ Па

V0 = P/aρ

ρ воды 1000 кг/м³

V0=539,55*10⁴ /0,06*1000 = 185245 м³

Vp = 392,4*10⁴ /0,06*1000 = 170040 м³

∆V = 185245-170040 = 15205 м³

Ответ. ∆V = 15205 м³

Задание 1.2

В вертикальной цилиндрической ёмкости диаметром D находится углеводородсодержащая жидкость, масса которой составляет m тонн, температура жидкости равна t ^оС, плотность r = 870 кг/м³. Определить на какую величину изменится уровень углеводородсодержащей жидкости в ёмкости и минимальную допустимую высоту этой ёмкости с целью недопущения перелива жидкости через верх, приводящего к загрязнению окружающей среды, если температура её изменится от 0 ^оС до 35 ^оС. Расширением стенок ёмкости пренебречь. Коэффициент температурного расширения жидкости принять равным b_t = 0,00075 1/ ^оС.

Исходные данные для задания 1.2:

№ варианта	Параметр
D, м	m ´ 103, кг
	3,3

Краткие указания: Способность капельной жидкости увеличивать или уменьшать свой первоначальный объём с изменением температуры характеризуется коэффициентом температурного расширения, который, в основном, зависит от рода капельной жидкости, его значение определяется с использованием справочной литературы.

Физический смысл коэффициента температурного расширения капельной жидкости – относительное изменение объёма жидкости при изменении её температуры на единицу.

Вариант 4

V= V0·(1+β_t ·dt),

при этом

ρ=ρ₀/(1+ β_t ·dt),

V0 = m/ ρ0 = 53*10³/870 = 60,9 м³

где V и V₀ - объемы, а ρ и ρ₀ - плотности соответственно при температурах t и t₀.

V= 60,9*(1+ 0,00075*35) = 62 м³

L - минимальная допустимая высота

L = 4V/πD²

L =4*62/3.14*3.3² = 7,2 м

Ответ. L =7,2 м

Задание 1.3

Капельная жидкость плотностью ρ=850кг/м³ перекачиваются по трубопроводу с внутренним диаметром d м, который должен не разрушаясь выдерживать манометрическое давление p атмосфер. Рассчитать минимальную толщину стенки трубопровода, принимая допустимое растягивающее напряжение в материале трубы s=85 МПа.

Исходные данные для задания 1.3:

№ варианта	Параметр
d, м	p, ат
	0,20

Краткие указания: Поверхность трубопровода представляет собой криволинейную (цилиндрическую) поверхность – жесткую оболочку. Сила избыточного гидростатического давления на внутреннюю поверхность трубопровода приводит к появлению растягивающих усилий в материале трубопровода, которые не должны вызывать в нём предельно допустимых напряжений. Растягивающие усилия в материале трубопровода возникают в результате действия горизонтальной составляющей силы гидростатического давления на цилиндрическую поверхность трубопровода, которая равна произведению манометрического давления в центре тяжести проекции криволинейной поверхности на вертикальную плоскость на площадь этой проекции. Жесткую оболочку (трубопровод) считать тонкой, т.е. с растягивающими напряжениями одинаковыми по всей толщине материала трубопровода.

Вариант 4

1ат = 1кГ/см² = 9,81 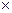10⁴

Толщину стенок стальных труб, работающих под действием внутреннего избыточного давления, определяют расчетом на прочность и прибавкой толщины на износ от коррозии. При этом пользуются формулой:

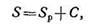
где S_Р — расчетная толщина стенки, мм;

С — прибавка к расчетной толщине на коррозию, мм

(для среднеагрессивных сред 2—5 мм).

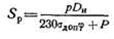
где р — внутреннее избыточное давление в трубопроводе,

D_H—диаметр трубы, мм;

σ_доп — допускаемое напряжение на разрыв;

φ — коэффициент прочности шва. Для бесшовных труб φ=1,

Р = 47*9,81*10⁴ =4,6 МПа

Sp = (850*40)/(230*85*10⁶*1+4.6*10⁶) = 17,3 мм

S = 17,3+4 = 21,3 мм

Ответ. S = 21,3мм

Задание 1.4

Для экстренной защиты от аварийно разливающихся жидких углеводородов используют быстровозводимые защитные ограждения различных конструкций. Определить силу гидростатического давления жидких углеводородов на единицу длины заграждения, если в поперечном сечении оно имеют форму равнобедренного треугольника, а также определить точку приложения силы (центр давления), если высота столба жидкости перед заграждением h м, а угол при основании равнобедренного треугольника составляет a градусов. Плотность жидких углеводородов r_у = 800 кг/м³.

Исходные данные для задания 1.4:

№ варианта	Параметр
h, м	a, град.
	0,4

 

Краткие указания: Сила гидростатического давления воды на поверхность заграждения рассчитывается для определения его устойчивости. Для этого, первоначально, рассчитывается избыточное давление в центре тяжести плоской фигуры на единице длины заграждения, а затем умножается на площадь этой фигуры. Для нахождения центра давления (глубины погружения точки приложения силы) определяется момент инерции плоской фигуры (в рассматриваемом случае – прямоугольника) с использованием справочников по гидравлике или сопромату.

Вариант 4

R = (р₀ + ρ·g·h_С) ·F, Н,

где р₀ – давление на свободную поверхность жидкости, Па;

ρ – плотность жидкости, кг/м³;

g – ускорение свободного падения, g = 9,81 м/с²;

h_С – глубина погружения центра тяжести щита под свободной поверхностью жидкости, м;

F – смоченная площадь, м².

Так как давление на свободную поверхность жидкости и внешнее давление на стенку равны атмосферному, то сила давления на стенку равна

R = ρ·g·h_С ·F, Н

Глубина погружения центра тяжести треугольного щита, который представляет собой равнобедренный треугольник, h_С = Н/3

Площадь F = В·H/2, м²,

где В – основание щита, м;

Н – высота щита, м.

Для нахождения основания В проводится перпендикуляр МN на основание. Делится на два прямоугольных равнобедренных треугольника. Очевидно, что В/2 = Н, а В = 2·H. Тогда

F= Н², м²

Таким образом,

R = ρ·g·Н/3·Н² = ρ·g·Н³/3 = 800*10*0,4/3*0,4²=666 Н

Глубина погружения центра давления h_О = Н/2

h_О = Н/2 = 0,4/2 = 0,2 м

Ответ. h_О = 0,2 м

Задание 1.5

Основание понтона, представляет собой цилиндр с положительной плавучестью. Определить объём надводной части цилиндра незагруженного понтона, не единице его длины, если диаметр поперечного сечения цилиндра составляет d м, плотность материала, из которого он изготовлен, равна r, а плотность воды r_в = 1000 кг/м³.

Исходные данные для задания 1.5:

№ варианта	Параметр
d, м	r, кг/м3
	0,23

Краткие указания: На тело, погружённое в жидкость, кроме его веса, действует выталкивающая сила, определяемая по закону Архимеда, как вес жидкости в объёме погружённой части тела. При решении задачи необходимо рассматривать равновесие тела, находящегося под действием этих двух сил.

Вариант 4

В случае неподвижности Fa = mg,

Vп = m/ρж = ρтV/ ρж.;

Vп/V = 0,5.

V = ¼ πd²h=0,041

h= 1

Vп = 530*0.25*3.14*0.0729/1000 = 1,7 м³

Ответ. Vп = 1,7 м³

Задания и краткие методические указания к их выполнению по гидродинамике

Задание 2.1

По напорному трубопроводу диаметром d м перекачивается мазут, имеющий кинематическую вязкость n = 1,5 Ст (стокс). Расход мазута составляет Q л/с. Определить режим движения жидкости.

Исходные данные для задания 2.1:

№ варианта	Параметр
d, м	Q, л/с
	0,20

Краткие указания: Для установления режима движения жидкости (ламинарный или турбулентный) необходимо определить число Рейнольдса (Re) и сравнить его с критическим числом для напорного потока.

1 Ст = 1 см²/с 1л = 1дм

Рейнольдсом опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее перечисленные выше факторы, где– кинематический коэффициент вязкости, м2/с. Точными измерениями установлено, что для круглых гладких труб критическим значением числа Рейнольдса является 2300, а для каналов некруглых сечений – 300. Если Re>Reкр, то режим движения – турбулентный, а при Re<Reкр – ламинарный

Вариант 4

Re = V*d/v

V = Q/(πd²/4) – скорость потока

V = 400/(3.14*400/4)=1,2 cм³

Re = 1,2*40/1,5 = 32

Ответ. Ламинарный

Задание 2.2

Определить режим движения воды в канале трапецеидального сечения. Ширина канала по дну составляет b м, глубина воды в канале h м, коэффициент заложения откосов боковых стенок m = 1,6. Расход воды в канале равен Q. Коэффициент кинематической вязкости воды в канале n_в равен 0,8 сСт (сантистокс).

Исходные данные для задания 2.2:

№ варианта	Параметр
b, м	h, м	Q, м3/с
	2,6	2,4	4,3

Краткие указания: Режим движения воды в канале определяется при помощи числа Рейнольдса (Re) для безнапорных потоков, в котором в качестве характеристики линейного размера принимается значение гидравлического радиуса. Гидравлический радиус – отношение площади живого сечения потока жидкости к смоченному периметру. Значение критического числа Рейнольдса принимается для безнапорных потоков. Угол заложения откосов представляет собой котангенс угла наклона боковых стенок канала к горизонту.

Вариант 4

arccot 1.6 = 36⁰

0.03 м³/с = 108 м³/ч

a = b - h · (ctg α + ctg β)

a = 2,6-2.4(1,37+1.37) = 0,5 м

с = h/ sin α

c = 2.4 /0.58 = 4,1 м

Скорость движения жидкости –120 м/сек

Re = V*h/v

Re = 120*2.4/0.8*10^-6 = 360*10^-6

Ответ. Ламинарный

Задание 2.3

Определить расход жидкости, пропускаемый самотечным напорным трубопроводом диаметром d и длиной l, если динамический коэффициент вязкости этой жидкости равен m, её плотность равна r, а разность отметок начальной и конечной точек трубопровода H составляет 2 м. Эквивалентная шероховатость стенок трубопровода D_э= 0,15 мм.

Исходные данные для задания 2.3:

№ варианта	Параметр
d, м	l, м	m, Па×с	r, кг/м3
	0,20		0,004

Краткие указания: При решении задачи необходимо использовать уравнение Бернулли и уравнение неразрывности потока (постоянства расхода), записанные для начального и конечного сечений трубопровода, задать режим движения жидкости в трубопроводе, определить её расход и проверить соответствие выбранному режиму движения жидкости по критерию Рейнольдса. В случае выявления несоответствия – выбрать другой режим движения жидкости и снова выполнить расчёт. Коэффициент гидравлического трения l следует определять по формуле Стокса для ламинарного режима движения жидкости или по одной из эмпирических формул для турбулентного режима движения жидкости, например, по формуле Альтшуля.

Вариант 4

Q= =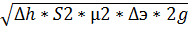

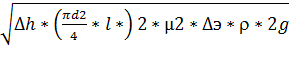
Q= = =262 л/с

Ответ. Q=262 л/с

Задание 2.4

Определить потери напора и давления по длине в новом стальном трубопроводе (эквивалентная шероховатость его стенок D_Э= 0,15 мм) диаметром d и длиной l, если по нему транспортируется вода с расходом Q = 400 л/с. Кинематическая вязкость воды n_в = 1 сСт, а её плотность r = 1000 кг/м³. Как изменятся потери напора и потери давления, если по нему будет транспортироваться нефть с тем же расходом? Коэффициент кинематической вязкости нефти n_н принять равным 1 Ст, а плотность r_н = 850 кг/м³.

Исходные данные для задания 2.4:

№ варианта	Параметр
d, м	l, м
	0,60

Краткие указания: Потери напора на трение по длине рассчитываются по формуле Дарси-Вейсбаха. Коэффициент гидравлического трения l в этой формуле определяется с учётом режима движения жидкости (см. указания к заданию 2.3). Потери напора с физической точки зрения представляют собой потери энергии на трение, отнесённые к единице веса жидкости, а потери давления представляют собой потери энергии, отнесённые к единице объёма жидкости.

Вариант 4

400 л/с = 24000 л/мин

Площадь сечения трубопровода: 2.82744E-7 кв.м
Относительная шероховатость трубопровода: 0.16666666666667
Скорость течения жидкости: 1414707.2970602 м/с
Число Рейнольдса: 848824378.23614
Режим течения: Турбулентный
Коэффициент гидравлического трения: 0.070283749912819

Потери напора по длине: 5.4*10¹⁶ м

Задание 2.5

В стальном трубопроводе длиной l, диаметром d, с толщиной стенок d равной 6 мм, средняя по сечению скорость воды V = 1,7 м/с. Определить наименьшее время закрывания запорной арматуры t_з, обеспечивающее повышение вызванного гидравлическим ударом давления в конце трубопровода не более 2,5 ат., не приводящего к разрыву трубопровода и нанесению ущерба окружающей среде. Как повысится давление в случае мгновенного перекрытия сечения трубопровода? Модуль упругости воды E_в = 2×10⁹ Па, модуль упругости стали E_с = 2×10¹¹ Па, плотность воды r_в = 1000 кг/м³. Определить потери напора на задвижке при движении жидкости с заданной скоростью V, если коэффициент местного сопротивления x будет равен 0,37.

Исходные данные для задания 2.5:

№ варианта	Параметр
d, м	l, м
	0,20

Краткие указания: При мгновенном перекрытии сечения трубопровода для определения ударного повышения давления используется формула Жуковского для прямого гидравлического удара. В случае постепенного закрытия запорной арматуры – зависимость для непрямого гидравлического удара. Потери напора при движении жидкости в местных сопротивлениях определяются по формуле Вейсбаха.

Вариант 4

Поделиться:

Воспользуйтесь поиском по сайту: