Значение кинематического коэффициента вязкости воды при различной температуре

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

(МИИТ)

 

Кафедра «Теплоэнергетика и водоснабжение на железнодорожном транспорте»

Автор: Кузьминский Р. А., кандидат военных наук, профессор

Приложение 2 к рабочей программе

ТЕМАТИКА КОНТРОЛЬНОЙ РАБОТЫ

И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕЕ ВЫПОЛНЕНИЮ

 

«ГИДРАВЛИКА И ГИДРОЛОГИЯ»

Направление/специальность: 271501.65 Строительство железных дорог, мостов и транспортных тоннелей _ _ _____

(код, наименование специальности /направления)

Профиль/специализация: Управление техническим состоянием железнодорожного пути

Квалификация (степень) выпускника: __ специалист ____ __ ____

Форма обучения: __ заочная___________ ______

 

Одобрена на заседании кафедры «Теплоэнергетика и водоснабжение на железнодорожном транспорте» Протокол №_____ «___» _____________ 20 ____ г. Зав. кафедрой _________ Р.А. Кузьминский (подпись, Ф.И.О.)

 

Москва 2013 г.

ВВЕДЕНИЕ

 

Контрольная работа нацелена на повышение эффективности и практической направленности обучения студентов. Выполнение контрольной работы содержит элементы исследования и способствует выработке навыков в принятии обоснованных технических решений.

Студенты выполняют 1 контрольную работу. Темой контрольной работы является: «Гидравлические и гидрологические расчеты на объекте строительства».

Контрольная работа содержит решение задач по следующим разделам:

Раздел 1 «Гидравлика»;

Раздел 2 «Гидрология».

По разделу 1 необходимо решить 7 задач, по разделу 2 необходимо решить 3 задачи.

Для каждой задачи дано десять вариантов исход­ных данных. Номер варианта выбирается по последней циф­ре учебного шифра. Даются также методические указания к решению задач.

Выполнению контрольной работы должно предшествовать изучение теоретических основ соответствующего раздела курса с использованием рекомендуемой литературы.

Контрольная работа может быть оформлена либо письменно на бумажном носителе, либо в электронно-цифровой форме на диске (CD). При представлении для рецензирования контрольной работы на электронном носителе (диске) студент обязан распечатать на бумажном носителе контрольную работу с титульным листом установленной формы и приложить к ней диск с содержанием работы. Титульный лист подписывается студентом, на нем производится регистрация работы. На титульном листе преподавателем проставляется отметка о допуске к защите и приводится рецензия контрольной работы.

При выполнении контрольной работы студент письменно либо в электронно-цифровой форме решает соответствующие шифру задачи.

При выполнении контрольной работы необходимо соблю­дать следующие условия:

Страницы рукописи должны быть пронумерованы.

Текст условия задачи следует приводить полностью.

Работу следует писать от руки чернилами или печатать на одной стороне листа.

Решения должны быть краткими, но исчерпывающими.

Решение задач вести поэтапно, с пояснением каждого хода решения.

При вычислении искомых величин необходимо написать расчетную формулу в буквенном выражении, подставить численные значения всех входящих в формулу параметров и привести окончательный ответ.

В приводимых расчетных формулах поясняют все вхо­дящие в них параметры.

Обозначения величин и терминология должны соответствовать принятым в учебниках.

У всех размерных величин должна быть проставлена размерность.

При решении задач следует строго следить за соблюде­нием единства размерностей величин, входящих в ту или иную расчетную зависимость.

Значение всех коэффициентов следует обосновать ссылкой на литературу с указанием автора, названия источника и номера страницы.

При оформлении ответов и решении задач обязательно выполнение необходимого иллюстрационного материала (графики, силовые и скоростные многоугольники, схемы потоков и т.д.).

Чертежи к работе, как правило, следует выполнять на миллиметровой бумаге и вклеивать или вшивать в работу.

При построении расчетных графиков нужно указать величины, откладываемые по осям графика, с обозначением их размерностей.

В конце работы привести список литературы, которой пользовался студент в процессе выполнения работы, с указанием автора, названия, места и года издания.

Все отмеченные рецензентом ошибки должны быть исправлены, а сделанные указания выполнены. Исправлять ошибки следует отдельно по каждой задаче на чистой сто­роне листа.

К дифференцированному зачету студент допускается только после защиты как контрольной рабо­ты, так лабораторных работ.

 

 

Раздел 1 «ГИДРАВЛИКА»

 

Задача 1.1

Задание.

С целью своевременного обнаружения и устранения воз­можных неплотностей в местах соединений перед сдачей в эксплуатацию трубопровод диаметром d и длиной l подвер­гается испытанию опрессовкой под действием избыточного давления р =2 МПа, достигаемого нагнетанием в трубо­провод дополнительного объема жидкости.

Требуется определить, какой объем жидкости дополни­тельно нужно подать в трубопровод для достижения необ­ходимого давления при испытании. Деформацией трубопро­вода пренебречь. Коэффициент объемного сжатия принять равным β_w=0,0005 1/МПа.

 

Исходные данные	Номер варианта
l, м
d, мм

 

Методические указания к решению задачи 1.1.

Для определения Δ W следует использовать формулу

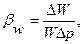
где β_w - коэффициент объемного сжатия жидкости;

Δ W - изменение объема жидкости;

W - первоначальный объем жидкости;

Δ р - изменение давления.

 

Задача 1.2

Задание.

В боковой вертикальной стенке резервуара есть прямо­угольное отверстие с раз­мерами а и b, перекрываемое плоским щитом, шарнирно закрепленным верхней стороной на горизонтальной оси, вокруг которой он может вращаться против часо­вой стрелки (рис. 1.2).

Требуется определить вес груза G на конце рычага длиной ℓ, жестко прикреп­ленного к щиту, который позволил бы щиту от­крываться при достижении водой в резервуаре уровня Н.

 

Рис. 1.2

Исходные данные	Номер варианта
a, м	0,4	0,6	0,5	0,8	0,7	0,9	1,0	0,6	0,5	0,4
b, м	0,5	0,6	0,7	0,8	0,7	0,9	1,0	0,7	0,6	0,6
H, м	2,0	2,5	3,0	3,5	4,0	4,0	4,5	3,0	2,5	3,0
l, м	1,0	1,0	1,1	1,3	1,2	1,5	1,5	1,1	1,0	1,1

Методические указания к решению задачи 1.2.

Необходимо найти величину и точку приложения силы из­быточного гидростатического давления на щит, после чего при­равнять момент силы Р относительно оси вращения при достиже­нии водой уровня H вращающему моменту от веса груза G и из этого равенства найти искомый вес груза G.

 

Задача 1.3

Задание.

В плоской вертикальной стенке резервуара, наполненного водой, есть прямоугольное отверстие высотой а и шириной b, пе­рекрываемое полуцилиндрической крышкой AВС (рис. 1.3). Верх­няя кромка этого отверстия находится на глубине H под уровнем воды в резервуаре.

Определить величину и линию действия силы избыточного гидростатического давления, действующей на цилиндрическую поверхность крышки AВС.

 

Рис. 1.3

 

Исходные данные	Номер варианта
H, м
R, м	0,5	1,0	0,75	0,6	0,75	0,6	0,70	1,0	0,75	0,5
b, м	1,0	2,0	1,5	2,0	2,5	2,0	2,4	2,5	2,0	1,5

 

Методические указания к решению задачи 1.3.

Суммарную силу избыточного давления воды на цилиндри­ческую поверхность определяют по формуле

,

где P_x - горизонтальнаясоставляющая силы избыточного гидростатического давления;

P_y - вертикальная составляющая силы избыточного гидростатического давления.

Горизонтальная составляющая силы избыточного гидроста­тического давления равна силе давления на вертикальную проек­цию цилиндрической поверхности

,

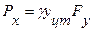где γ - объемный вес воды; γ ≈10 кН/м³;

y_цт - расстояние по вертикали от центра тяжести верти­кальной проекции цилиндрической поверхности до уровня воды;

F_y - площадь вертикальной проекции цилиндрической поверхности.

Вертикальную составляющую силы избыточного гидроста­тического давления определяют по формуле

P_y= W,

где γ - объемный вес воды; γ ≈10 кН/м³;

W - объем тела давления.

Иными словами, вертикальная составляющая силы давле­ния равна весу жидкости в объеме тела давления.

Тело давления представляет собой объем, расположенный над цилиндрической поверхностью и заключенный между верти­кальными плоскостями, проходящими через крайние образующие цилиндрической поверхности, самой цилиндрической поверхно­стью и свободной поверхностью воды.

Если тело давления расположено со стороны смачиваемой жидкостью поверхности (в теле давления находится вода), то оно положительно и сила P_y будет направлена вниз.

Если тело давления находится со стороны не смачиваемой жидкостью поверхности (в теле давления нет воды), то такое тело давления отрицательно и сила P_y будет направлена вверх.

В данной задаче для нахождения тела давления следует ци­линдрическую поверхность АВС разделить на две: АВ и ВС; при­чем тело давления для поверхности АВ будет отрицательным, а для ВС - положительным.

Результирующий объем тела давления на всю цилиндриче­скую поверхность АВС и его знак находятся путем алгебраическо­го суммирования тел давления на криволинейные поверхности АВ и ВС.

Суммарная сила избыточного гидростатического давления на цилиндрическую поверхность направлена по радиусу к центру цилиндрической поверхности под углом φ к горизонту:

.

 

Задача 1.4

Задание.

Из открытого резервуара, в котором поддерживается посто­янный уровень, по стальному трубопроводу (эквивалентная шеро­ховатость k_э =0,1 мм), состоящему из труб различного диаметра d и различной длины l, вытекает в атмосферу вода, расход кото­рой Q, температура t° С (рис. 1.4.1).

Требуется:

1. Определить скорости движения воды и потери напора (по длине и местные) на каждом участке трубопровода.

2. Установить величину напора H в резервуаре.

3. Построить напорную и пьезометрическую линии на всех участках трубопровода

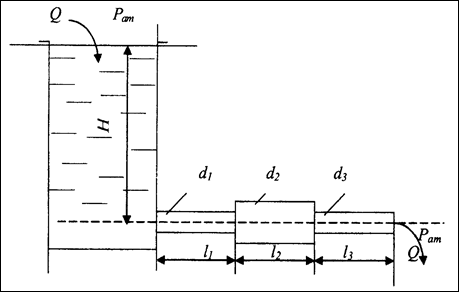
Рис. 1.4.1

 

Исходные данные	Номер варианта
Q, л/с	0,5	1,0	1,5	2,0	2,5	3,0	3,0	4,0	4,5	5,0
d1, мм
d2, мм
d3, мм
l1, м	1,0	2,0	1,5	2,0	3,0	2,5	5,0	4,0	5,0	2,0
l2, м	2,0	2,0	3,0	4,0	4,0	5,0	2,5	4,0	5,0	4,0
l3, м	1,0	2,0	2,5	3,0	5,0	2,5	5,0	4,0	6,0	6,0
t, °С

 

Методические указания к решению задачи 1.4.

Эту задачу решают на основе применения уравнения Д. Бернулли. Для плавно изменяющегося потока вязкой жидкости, движущейся от сечения 1 к сечению 2, уравнение Д. Бернулли имеет вид

,

где z₁ и z₂ - расстояния от произвольно выбранной гори­зонтальной плоскости сравнения до центров тяжести живых сечений 1 и 2;

p₁ и p₂ - давления в центрах тяжести живых сечений 1 и 2;

V_i и V₂ - средние скорости движения жидкости в живых сечениях 1 и 2;

α₁ и α₂ - коэффициенты кинетической энергии (коэффициенты Кориолиса) - поправочные коэффициенты, представляющие собой безразмерную величину, равную отношению истинной кинетической энергии потока в рассматриваемом сечении к кинетической энергии, посчитанной по средней скорости. Для турбулентного режима движения значение а можно принять равным 1;

h₁.₂ - потери напора на преодоление сил сопротивле­ния при движении потока от сечения 1 до сече­ния 2;

γ=ρg - удельный вес жидкости;

ρ - плотность жидкости;

g - ускорение свободного падения.

Решение задачи выполняют в следующем порядке:

1. Составляют уравнение Д. Бернулли в общем виде для се­чений 0-0 и 3-3. Сечение 0-0 совпадает со свободной поверх­ностью жидкости в резервуаре, сечение 3-3 -выходное сечение. При написании уравнения Д. Бернулли следует помнить, что ин­дексы у всех членов уравнения должны быть одинаковыми с на­званием сечений, к которым они относятся. Например, величины, относящиеся к сечению 0- 0, следует обозначить z₀, p₀, α ₀, V_{0 .}

2. Намечают горизонтальную плоскость сравнения. При го­ризонтальном трубопроводе в качестве таковой берут плоскость, проходящую по оси трубопровода. После этого устанавливают, чему равно каждое слагаемое, входящее в уравнение Д. Бернулли, применительно к условиям решаемой задачи. Например, z₀=H (искомая величина напора в резервуаре); p₀=p_a (атмосферное давление); V₀ (скорость движения воды в резервуаре) и т. д.

3. После подстановки всех найденных величин в уравнении Д. Бернулли и его преобразования записывают расчетное уравнение в буквенном выражении для определения искомой величины H.

4. Определяют скорость движения воды на каждом участке.

5. По скоростям движения воды вычисляют числа Рейнольдса и устанавливают режим движения на каждом участке. Значение кинематического коэффициента вязкости следует взять из Приложения 1.

6. Определяют потери напора по длине каждого участка (h_l1, h_l2, h_l3) и в каждом местном сопротивлении: вход в трубу из резервуара h_вх, внезапное расширение h_вр и внезапное сужение h_вс.

Потери напора по длине следует определять по формуле Дарси

,

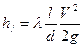где l – длинна расчетного участка;

d – диаметр трубопровода;

V – средняя скорость движения потока на рассматриваемом участке;

λ – коэффициент гидравлического трения (коэффициент Дарси), учитывающий влияние на потерю напора по длине вязкости жидкости и шероховатости стенки трубы; его определяют по различным формулам в зависимости от зоны (области) сопротивления, в которой работает трубопровод.

При значении критерия зоны турбулентности трубопровода работает в зоне гидравлически гладких труб и значение λ следует определять по формуле Блазиуса

,

где - число Рейнольдса;

ν - кинематический коэффициент вязкости, определяемый в зависимости от температуры по Приложению 1.1.

При трубопровод работает в переходной зоне сопротивления, в которой определяют по формуле Альтшуля

.

При 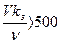имеет место квадратичная зона сопротивления, и значение λ определяется по формуле Шифринсона

.

Потери напора в местных сопротивлениях вычисляют по формуле Вейсбаха

,

где V – средняя скорость за данным сопротивлением;

ζ - безразмерный коэффициент местного сопротивления (берут по справочнику).

При вычислении потери напора на входе в трубу коэффициент местного сопротивления ζ _вх=0,5.

Значение коэффициента местного сопротивления при внезапном сужении трубопровода

,

где ω₁ – площадь широкого сечения трубы;

ω₂ – площадь узкого сечения трубы.

Потерю напора при внезапном расширении трубопровода можно определить по формуле Борда

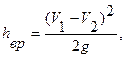
где V₁ и V₂ - средние скорости течения соответственно до и после расширения.

7. После определения потерь напора по длине и в местных со­противлениях вычисляют искомую величину - напор Н в резер­вуаре.

8. Строят напорную линию. Напорная линия показывает, как изменяется полный напор 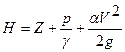(полная удельная энергия) по длине потока. Значения Н откладывают от осевой линии трубопровода.

При построении напорной линии нужно вертикалями выде­лить расчетные участки. Таких участков в данной задаче будет три. Далее в произвольно выбранном вертикальном масштабе откладывают от осевой линии величину найденного уровня жид­кости в резервуаре Н. Проводя по этому уровню горизонтальную линию, получаем линию исходного (первоначального) напора. От уровня жидкости в резервуаре по вертикали, отвечающей сечению при входе жидкости в трубопровод, откладывают в масштабе вниз отрезок, равный потери напора при входе жидкости в трубу (потеря напора в местном сопротивлении).

На участке l₁ имеет место потеря напора по длине трубопро­вода h_ℓ1. Для получения точки, принадлежащей напорной линии в конце участка l₁, нужно от линии полного напора после входа жидкости в трубу отложить по вертикали в конце участка l₁ вниз в масштабе отрезок, соответствующий потере напора на участке l₁. Затем от точки полного напора в конце участка l₁ откладывается в масштабе по вертикали отрезок, соответствующий потере напора в местном сопротивлении (внезапное расширение или сужение), и так до конца трубопровода. Соединяя точки полного напора, получим напорную линию.

Пьезометрическая линия показывает, как изменяется пьезо­метрический напор z+ р/γ (удельная потенциальная энергия) по длине потока. Удельная потенциальная энергия меньше полной удельной энергии на величину удельной кинетической энергии aV²/(2g). Поэтому, чтобы построить пьезометрическую линию, нужно вычислить на каждом участке величину aV²/(2g) и отложить ее числовое значение в масштабе вниз по вертикали от напорной линии. Откла­дывая соответствующие значения aV²/(2g) в начале и в конце каж­дого участка и соединяя полученные точки, строим пьезометриче­скую линию.

График напорной и пьезометрической линий будет построен правильно в том случае, если при их построении были выдержаны принятые вертикальный и горизонтальный масштабы, а также верно вычислены все потери напора и все скоростные напоры αV²/(2g).

После построения напорной и пьезометрической линий на графике показывают все потери напора и все скоростные напоры с указанием их численных значений. Примерный вид графика приведен на рис. 1.4.2.

 

 

Рис. 1.4.2

Задача 1.5

Задание.

Горизонтальный трубопровод из стальных труб, схема ко­торого показана на рис. 1.5, имеет участок с параллельным соеди­нением труб, состоящим из двух линий длиной l₁ и l₂ и диаметрами d₁ и d₂. В точках В, С и D заданы расходы воды Q_B, Q_C и Q_D.

Требуется:

1. Установить диаметры труб на участках АВ и СD по пре­дельным расходам.

2. Определить распределение расходов по 1-й и 2-й линиям параллельного соединения трубопроводов.

3. Определить необходимый напор в точке А для обеспече­ния заданных расходов Q _B, Q _C и Q _D при заданном свободном на­поре (превышении пьезометрической линии над поверхностью земли) в конце трубопровода H _св, если известны длины участков АВ и СD.

4. Построить пьезометрическую линию по длине трубопро­вода.

Рис. 1.5

 

Исходные данные	Номер варианта
l1, м
l2, м
lАВ , м
lCD, м
d1, мм
d2, мм
QB, л/с
QC, л/с
QD, л/с
Hсв , м

Методические указания к решению задачи 1.5.

Решение задачи рекомендуется выполнять в следующем по­рядке:

1. Подсчитывают расчетные расходы на каждом участке. При этом следует помнить, что расчетный расход на участке равен сумме узловых расходов, расположенных за данным участком (по направлению движения воды).

2. По предельным расходам, приведенным в Приложении 1.2, опре­деляются диаметры труб на участках АВ и СD.

3. Зная общий расход, проходящий по участку с параллель­ным соединением трубопроводов, а также длины l₁ и l₂ и диаметры d₁ и d₂ каждой линии этого участка, определяют потерю напора в параллельно соединенных трубопроводах.

Параллельным соединением трубопроводов называется такое соединение, когда две или более линий трубопровода имеют общие начальную и конечную точки.

Расчет параллельного соединения трубопроводов основан на двух положениях:

h_ℓ1=h_ℓ2=…=h_ℓn, (потери напора на всех параллельно со­единенных участках одинаковы) и Q₁+Q₂=Q_BC (суммарный рас­ход, проходящий по участкам параллельного соединения трубо­проводов).

С другой стороны по формуле Шези имеем

,

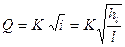где К – расходная характеристика (модуль расхода) трубы, определяемая по Приложению 3).

Следовательно

где К₁ и К₂ - расходные характеристики труб на участках 1 и 2 определяемые по Приложению 1.3;

l₁ и l₂ - длины участков 1 и 2.

Отсюда потеря напора на участке с параллельным соединением труб:

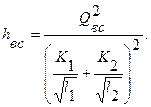
4. Затем вычисляют расходы, проходящие по каждой линии параллельного соединения

и выполняется проверка

Q₁+Q₂ =Q_BC.

5. Определяют потери напора на участках АВ и СD

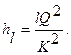
6. Зная заданный свободный напор в точке D, а также потери напора на каждом участке, определяют значения напоров в точках C, B и А:

H_C= H_СВ+h_CD;

H_B=H_C+h_BC;

H_A=H_B+h_AB,

где h_CD, h_BC, h_AB - ранее вычисленные потери напора на каждом участке.

7. По полученным значениям напоров в точках А, В, С и D строят пьезометрическую линию.

Задача 1.6

Задание.

Трапецеидальный канал с крутизной откосов т и коэффи­циентом шероховатости стенок п =0,025, имеющий ширину по дну b, проложен с уклоном дна i (рис. 1.6).

Требуется определить:

1. Глубину воды в канале при пропуске расхода Q.

2. Ширину канала по верху (по урезу воды) B.

3. Среднюю скорость движения воды V.

4. Состояние потока (спокойное или бурное).

5. Критический уклон дна канала i_к.

6. Для найденного значения площади поперечного сечения найти гидравлически наивыгоднейшее сечение канала (отношение b/h, соответствующее гидравлически наивыгоднейшему сечению).

7. Определить пропускную способность найденного гид­равлически наивыгоднейшего сечения.

 

Рис. 1.6

 

Исходные данные	Номер варианта
m		1,25	1,5	2,0	1,25		1,5			1,25
b, м		2,5					3,5			5,5
i,	0,0001	0,0005	0,0004	0,001	0,0015	0,002	0,0025	0,003	0,0002	0,005
Q,, м3/с

 

Методические указания к решению задачи 1.6.

Искомую глубину воды в канале при пропуске расхода Q можно определить двумя способами: методом подбора по формуле Шези и с помощью гидравлического показателя русла.

Метод подбора заключается в следующем.

Задаваясь раз­личными значениями h, вычисляем последовательно

площадь живого сечения потока ω = h (b+тh),

длину смоченного периметра русла ,

гидравлический радиус ,

коэффициент Шези ,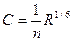

расходную характеристику К = ;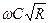

расход .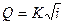

Все вычисления сводят в таблицу.

 

h, м	ω, м2	χ, м	R, м	C, м0,5/с	K, м3/с	Q, м3/с	lgK	lgh	lgK1-lgK2	lgh1- lgh2	x

 

По данным таблицы строится график h= ƒ(Q), пользуясь которым по заданному значению Q определяют искомое значение h.

Второй способ заключается в использовании показательного закона, по которому

где h₁ и h₂ - некоторые произвольные глубины;

K₁ и K₂ – соответствующие этим глубинам расходные характеристики;

x – гидравлический показатель русла, характеризующий поперечное сечение русла, определяемый по формуле

Величину гидравлического показателя русла, вычисленную для нескольких пар глубин, записывают в сводную таблицу, далее на основании произведенных вычислений определяют среднее значение гидравлического показателя русла х, по которому, используя показательный закон, находят искомую глубину воды в канале.

где h₁ - любая произвольная глубина воды в канале;

K₁ - соответствующая этой глубине расходная характеристика;

- заданное значение расходной характеристики (Q и i - заданные значения расхода и уклона).

Предлагается сравнить результаты, полученные 1-м и 2-м способами.

После нахождения глубины определяют ширину канала по верху

B=b+2mh

и среднюю скорость движения воды

Состояние потока может быть определено по одному из двух параметров: по критической глубине h_к или по безразмерному числу Фруда Fr.

При глубине потока h>h _к - поток находится в спокойном со­стоянии, при h<h _к - поток находится в бурном со­стоянии.

При критической глубине должно соблюдаться равенство

.

Исходя из площади живого сечения потока , находят величины b и h, отвечающие гидравлически наивыгоднейшему сечению канала.

Зная b и h, по формуле Шези определяют пропускную спо­собность гидравлически наивыгоднейшего сечения.

 

Задача 1.7

Задание.

Дорожная насыпь, имеющая высоту Н_нас, ширину земляного полотна В =12 м и крутизну заложения откосов m =1,5, пересека­ет водоток с переменным расходом, для пропуска которого в теле насыпи укладывают с уклоном i _т круглую железобетонную трубу, имеющую обтекаемый оголовок.

Требуется:

1. Подобрать диаметр трубы для пропуска максимального расчетного расхода Q _max в напорном режиме при допустимой ско­рости движения воды в трубе V_доп= 4 м/с и минимально допусти­мом расстоянии от бровки насыпи до подпорного уровня а= 0,5 м.

2. Определить фактическую скорость движения воды в тру­бе V_ф при пропуске максимального расхода и глубину Н перед трубой, соответствующую этому расходу.

3. Рассчитать предельные расходы и соответствующие им глубины перед трубой, при которых труба будет работать в безна­порном и полунапорном режимах.

 

Исходные данные	Номер варианта
Qmax, м3/с	4,5	б		3,9	14,5		12,8	1,7	9,6
Hнас,м	3,0	2,6	3,2	3,6	5,0	2,6	4,1	2,4	5,4	4,0
i т	0,008	0,003	0,020	0,006	0,004	0,010	0,003	0,015	0,012	0,005

Методические указания к решению задачи 1.7.

Водопропускные трубы под насыпями дорог (железных и автомобильных) служат для пропуска расходов воды периодиче­ски действующих водотоков во время ливневых или весенних паводков.

В настоящее время чаще всего применяются водопропуск­ные трубы круглого сечения.

По числу отверстий трубы бывают одноочковые, двухочковые, трехочковые и многоочковые.

Согласно действующим типовым проектам, круглые дорож­ные водопропускные трубы имеют следующие стандартные отвер­стия: 0,75; 1,0; 1,25; 1,5 и 2 м.

Одной из задач гидравлического расчета труб является оп­ределение необходимого диаметра труб. При этом считается, что пропускная способность многоочковых (двухочковых, трехочковых и т.д.) труб равна суммарной пропускной способности соот­ветствующего количества одноочковых труб.

Гидравлические расчеты водопропускных труб выполняют в зависимости от условий их работы.

Различают следующие режимы работы труб:

1) безнапорный, когда входное сечение не затоплено и на всем протяжении трубы поток имеет свободную поверхность (рис. 1.7.1, а);

2) полунапорный, когда входное сечение трубы затоплено, т.е. на входе труба работает полным сечением, а на остальном протяжении поток имеет свободную поверхность (рис. 1.7.1, б);

3) напорный, когда труба работает полным сечением, т.е. все поперечное сечение трубы по всей длине полностью заполнено водой (рис. 1.7.1, в).

 

Рис. 1.7.1

 

Безнапорным режим бывает при условии

,

где Н - напор (глубина) воды перед трубой;

d - диаметр трубы.

Пропускная способность безнапорных труб может быть оп­ределена по формуле А.А. Угинчуса

где μ - коэффициент расхода (принять μ =0,335);

b_к - средняя ширина потока в сечении с критической глубиной (определяется по графику, представлен­ному на рис. 1.7.2).

 

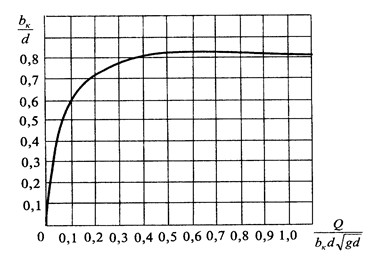
Рис. 1.7.2

 

Полунапорный режим бывает при условии

Н>1,2d.

Пропускная способность полунапорных труб с учетом укло­на дна определяется по формуле

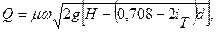
где μ - коэффициент расхода, зависящий от типа оголовка (для условий данной задачи принять μ =0,7);

ω - площадь сечения трубы;

d - диаметр отверстия трубы;

i_T - уклон дна трубы.

Пропускная способность полунапорных труб больше, чем безнапорных.

Напорный режим имеет место при одновременном выпол­нении трех условий:

1) входной оголовок должен быть обтекаемым;

2) Н >1,4d;

3) i_т<i, где i - гидравлический уклон.

Пропускную способность напорных труб вычисляют по формуле

Коэффициент расхода μ определяют зависимостью