Свойства дифференцируемых функций

Дифференцирование функций одного действительного переменного.

Определение и геометрическая интерпретация первой производной

 

Если f – функция одного переменного и x ₀ ∈ (a, b), то функция φ такая, что

называется разностным отношением функции f в точке x ₀.

Геометрическая интерпретация. Пусть на графике функции f в координатной системе x, y фиксированная точка P ₀ (x ₀, y ₀) и подвижная точка P (x, y), и пусть секущая, проведенная через эти точки, образует угол β с положительным направлением оси x. Тогда

.

Разностное отношение функции f в точке x ₀ равно, таким образом угловому коэффициенту секущей, проведенной через точки P и P ₀.

Функция f называется дифференцируемой в точке x ₀ ∈ (a, b), если существует предел разностного отношения функции f в точке x ₀:

φ (x) = .

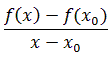Этот предел называется производной функции f в точке x ₀. Обозначение:

.

Геометрическая интерпретация: Если на графике функции подвижная точка P (x, y) стремится к точке P ₀ (x ₀, y ₀), то изменяется также угловой коэффициент секущей. Если существует производная функции f в точке x ₀, то прямую, проходящую через точку P ₀ (x ₀, y ₀) и такую, что tg (α) = f ' (x ₀), где α — угол наклона этой прямой, называют касательной к графику функции f в точке P ₀ (x ₀, y ₀). таким образом уравнение касательной есть y – f (x ₀) = f ' (x ₀)(x – x ₀).

Функция f называется дифференцируемой справа (слева) в точке x ₀, если существует предел справа (слева) 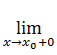φ (x) ( φ (x)) разностного отношения в точке x ₀. Этот предел называется производной справа (слева) функции f в точке x ₀ и обозначается f ' ₊(x ₀), f ' (x ₀ + 0) (f ' _–(x ₀), f ' (x ₀ – 0)).

Если существует f ' (x ₀), то функция f дифференцируема справа и слева в точке x ₀ и f ' ₊(x ₀) = f ' _–(x ₀) = f ' (x ₀). Обратно, если существуют односторонние производные f ' ₊(x ₀), f ' _–(x ₀) и f ' ₊(x ₀) = f ' _–(x ₀) то существует также f ' (x ₀) = f ' ₊(x ₀) = f ' _–(x ₀).

Функция f называется дифференцируемой на множестве E, если она дифференцируема во всех точках x ₀ ∈ E. Функция f называется дифференцируемой, если она дифференцируема на D (f). Если f дифференцируема, то функция f ', определенная соответствием x → f ' (x), называется производной функции f.

Производные высших порядков

 

Пусть производная f ' функции f дифференцируема в точке x ₀ ∈ D (f '). Тогда (f ' (x))| _{x = x 0} называется второй производной функции f в точке x ₀. Обозначение:

f '' (x ₀) = f ⁽²⁾(x ₀) = f (x ₀).

Действуя подобным образом, определяют n-ю производную, или производную n-го порядка функции f в точке x ₀:

f ⁽ⁿ⁾(x ₀) = (f ^{(n – 1)} (x))| _{x = x 0} = f (x ₀).

Если существует f ⁽ⁿ⁾(x ₀), то функция f называется n раз дифференцируемой в точке x ₀. Имеет место следующее равенство:

(f ⁽ⁿ⁾(x))^(m)| _{x = x 0} = f ^{(n + m)}(x ₀).

Функция f называется n раз непрерывно дифференцируемой на множестве E, если она n раз дифференцируема в каждой точке x ∈ E и f ⁽ⁿ⁾ непрерывна на E.

Свойства дифференцируемых функций

 

1. Функция, дифференцируемая в точке x ₀, непрерывна в этой точке.

2. Пусть функции f ₁ и f ₂ дифференцируемы в точке x ₀. Тогда функция c ₁ f ₁ + c ₂ f ₂, где c ₁, c ₂ ∈ R, также дифференцируема в точке x ₀ и

(c ₁ f ₁ + c ₂ f ₂)'| _{x 0} = c ₁ f '₁ (x ₀) + c ₁ f '₂ (x ₀).

Произведение f ₁ f ₂ также дифференцируемо в точке x ₀ и имеет место следующее правило дифференцирования произведения:

(f ₁ f ₂)'| _{x 0} = f '₁ (x ₀) f ₂ (x ₀) + f ₁ (x ₀) f '₂ (x ₀).

Если f ₂ (x ₀) ≠ 0, частное f ₁ / f ₂ дифференцируемо в точке x ₀ и имеет место следующее правило дифференцирования дроби:

3. Пусть функции f и φ дифференцируемы соответственно в x ₀ и t ₀ и x ₀ = φ (t ₀). Тогда сложная функция f (φ (t ₀)) дифференцируема в точке t ₀ и обладает производной

(f (φ))'| _{t = t 0} = f ' [φ (t ₀)] · φ' (t ₀).

4. Пусть функция f дифференцируема и строго монотонна на (a, b). Пусть также в точке x ₀ ∈ (a, b) производная f '(x ₀) ≠ 0. Тогда обратная функция g (y) дифференцируема в точке y ₀ = f (x ₀) и ее производная есть

(g (y))'| _{y = y 0} =

5. Если функции f ₁ и f ₂ n раз дифференцируемы в точке x ₀, то функция f ₁ f ₂ также n раз дифференцируема в точке x ₀ и имеет место формула Лейбница:

если считать, что f_i ⁽⁰⁾ (x ₀) = f_i (x ₀) (i =1,2).

 

Для функций, дифференцируемых в интервале, имеют место следующие теоремы.

Теорема Ролля. Если функция непрерывна на отрезке [ a, b ] и дифференцируема на интервале (a, b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Геометрический смысл. Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

Теорема Лагранжа (о конечном приращении). Если функция f непрерывна на [ a, b ] и дифференцируема на (a, b), то найдется по крайней мере одна точка x ₀ ∈ (a, b), в которой

f (x ₀) =

Геометрический смысл. Если для функции f выполняются условия теоремы Лагранжа, то к графику функции f можно провести по меньшей мере одну касательную, параллельную секущей, проведенной через точки (a, f (a)), (b, f (b)).

Теорема Коши. Пусть функции f и g непрерывны на [a, b], дифференцируемы в (a, b), и пусть g '(x) ≠ 0 для всех x ∈ (a, b), Тогда существует по крайней мере одна точка x₀ ∈ (a, b), в которой

Поделиться:

Воспользуйтесь поиском по сайту: