 |
Условия равновесия плоской системы сил.
|
|
|
|
Лекция 5
Краткое содержание: Приведение силы к заданному центру. Приведение системы сил к заданному центру. Условия равновесия пространственной системы параллельных сил. Условия равновесия плоской системы сил. Теорема о трех моментах. Статически определимые и статически неопределимые задачи. Равновесие системы тел.
ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
Приведение силы к заданному центру.
Равнодействующая системы сходящихся сил непосредственно находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку.
Теорема о параллельном переносе силы. Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.
Пусть сила 
приложена в точке A. Действие этой силы не изменяется, если в точке B приложить две уравновешенные силы. Полученная система трех сил представляет собой силу 
равную , но приложенную в точке В и пару 
с моментом 
. Процесс замены силы силой и парой сил называется приведением силы к заданному центру В.
Приведение системы сил к заданному центру.
Основная теорема статики (Пуансо).
Любую произвольную систему сил, действующую на твердое тело, можно в общем случае привести к силе и паре сил. Этот процесс замены системы сил одной силой и одной парой сил называется приведением системы сил к заданному центру.
|
|
|
Главным вектором системы сил называется вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.
Формулы для вычисления главного вектора и главного момента
Формулы для вычисления модуля и направляющих косинусов
Главного вектора и главного момента
Условия равновесия системы сил.
Векторная форма.
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю.
Алгебраическая форма.
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.
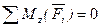
Условия равновесия пространственной системы
Параллельных сил.
На тело действует система параллельных сил. Расположим ось Oz параллельно силам.
Уравнения 
Для равновесия пространственной системы параллельных сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций этих сил была равна нулю и суммы моментов этих сил относительно двух координатных осей, перпендикулярным силам, также были равны нулю.
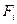-проекция силы на ось Oz.
ПЛОСКАЯ СИСТЕМА СИЛ.
Условия равновесия плоской системы сил.
На тело действует плоская система сил. Расположим оси Ox и Oy в плоскости действия сил.
Уравнения 
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма моментов этих сил относительно любой точки, находящейся в плоскости действия сил также была равна нулю.
|
|
|
Теорема о трех моментах.
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.
|
|
|
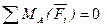
