 |
Анализ многомерных рядов распределения.
|
|
|
|
Анализ одномерных рядов распределения.
ЗАДАЧА № 10
а) Строим интервальный ряд, количество интервалов – 10.
Размах вариации равен: 
Величина интервала равна: 
, и, для удобства расчетов округляяем до целого значения = 940.
Получаем следующий интервальный вариационный ряд (Таблица 1)
Таблица 1
| Интервал по объему кредитных вложений, млрд. руб. | Середина интервала, (хi) | Количество банков, (fi) | 
| Накопленные частоты, (fi’) | 
|
| 40 - 980 | |||||
| 980 - 1920 | 138990,28 | ||||
| 1920 - 2860 | 4354734,2 | ||||
| 2860 - 3800 | |||||
| 3800 - 4740 | |||||
| 4740 - 5680 | |||||
| 5680 - 6620 | |||||
| 6620 - 7560 | |||||
| 7560 - 8500 | |||||
| 8500 - 9440 | |||||
| Сумма |
б) Строим графики:
в) Вычисляем необходимые показатели распределения:
1.Ряд распределения является вариационным, поэтому расчет среднего значения будет произведен по формуле:
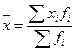, где xi – середина интервала; fi – частота.
Получаем 
Мода рассчитывается по формуле:
, где
x0 – нижняя граница модального интервала (интервала с максимальной частотой);
i – величина интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала предшествующего модальному;
fMo+1 – частота интервала следующего за модальным.
Получаем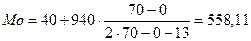 
Медиана рассчитывается по формуле:
, где
x0 - нижняя граница медианного интервала (интервал, где f’>åf/2);
f’Me – 1 – накопленная частота интервала, предшествующего интервальному;
fMе – частота медианного интервала;
i – величина интервала.
Получаем 
Мы видим, что 
, следовательно, ряд не соответствует нормальному распределению. Из полигона и гистограммы видно, что распределение асимметричное.
|
|
|
Мы видим, что 
, следовательно, ряд имеет высокую асимметрию.
2.Находим показатели вариации:
Дисперсия будет находиться, используя данные таблицы 1 по формуле:
Получаем 
Среднее квадратичное отклонение находится по формуле:
Получаем 
Коэффициент вариации находится по формуле: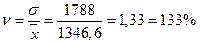 
Коэффициент вариации показывает, что вариация очень высокая и ряд нельзя считать однородным.
3. Рассчитываем F- критерий Фишера.
Для этого разобьем исходный ряд на две выборки: n1 =63, n2 = 37 и по этим выборкам определим дисперсию:
Таблица 2
| 
| |||||||||||
Определяем расчетное значение F- критерия Фишера:
Для степеней свободы V1 = n1 – k – 1 = 63 – 2 –1 = 60 и V2 = n2 – k –1 = 37 – 2 – 1=34 находим по таблице значений F, что Fтабл = 1,76.
, следовательно, ряд нельзя считать однородным.
Рассчитаем Т – критерий Грабса для каждого значения по формуле: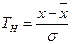 
Получаем следующую таблицу значений:
Таблица 3
| 3,50 | 1,99 | 0,37 | 0,22 | 0,71 | 0,04 | 0,47 | 0,48 | 0,49 | 0,69 |
| 4,52 | 4,30 | 0,07 | 0,62 | 0,43 | 0,57 | 0,49 | 0,68 | 0,71 | 0,66 |
| 1,66 | 0,22 | 0,08 | 0,14 | 0,42 | 0,65 | 0,67 | 0,62 | 0,62 | 0,46 |
| 2,22 | 0,86 | 0,45 | 0,54 | 0,50 | 0,53 | 0,64 | 0,61 | 0,60 | 0,67 |
| 1,43 | 0,14 | 0,67 | 0,55 | 0,70 | 0,48 | 0,38 | 0,62 | 0,62 | 0,65 |
| 2,09 | 0,14 | 0,17 | 0,67 | 0,79 | 0,38 | 0,65 | 0,31 | 0,73 | 0,52 |
| 1,07 | 0,23 | 0,14 | 0,19 | 0,38 | 0,45 | 0,32 | 0,37 | 0,56 | 0,70 |
| 1,16 | 0,50 | 0,83 | 0,23 | 0,36 | 0,53 | 0,60 | 0,52 | 0,59 | 0,58 |
| 0,32 | 1,72 | 0,47 | 0,00 | 0,44 | 0,44 | 0,69 | 0,28 | 0,59 | 0,68 |
| 2,61 | 0,20 | 0,43 | 0,58 | 0,69 | 0,63 | 0,47 | 0,73 | 0,56 | 0,68 |
|
|
|
Максимально допустимое значение T-критерия Грабса Тн = 2,52. Следовательно, можно выделить следующие аномальные явления: 3,50; 4,52; 4,30.
4.Рассчитаем показатели асимметрии и эксцесса. Для этого заполним таблицу 4:
Таблица 4
| xi | fi | 
| 
|
| -40987518032,72 | 34290157586173,50 | ||
| 14371594,95 | 1486022918,04 | ||
| 4543729706,02 | 4740927575257,10 | ||
| 23407346357,11 | 46426130764696,00 | ||
| 74952475754,71 | 219116067621325,00 | ||
| 172993697472,31 | 668343850814530,00 | ||
| 110827174503,30 | 532347250009170,00 | ||
| 0,00 | 0,00 | ||
| 298533012181,70 | 1995215533615200,00 | ||
| 886086498361,81 | 6754991811611410,00 | ||
| Сумма | 1530370787899,20 | 10255473215620700,00 |
Коэффициент асимметрии определяем по формуле:
Аs>1, следовательно, асимметрия левосторонняя высокая
Коэффициент эксцесса определяем по формуле:
Es>3, следовательно эксцесс высокий, островершинный.
Рассчитываем критерий Колмогорова:
- Среднее квадратичное отклонение равно 
- определяем нормированные отклонения: 
- находим ft по таблице:
- рассчитываем теоретические значения частот: 
- рассчитываем накопленные частоты.
Таблица 5
| Интервал | Середина интервала, (х) | f | t | ft | fтеор | f’ | fтеор’ |
| 40 - 980 | 0,47 | 0,3572 | |||||
| 980 - 1920 | 0,06 | 0,3989 | |||||
| 1920 - 2860 | 0,58 | 0,3372 | |||||
| 2860 - 3800 | 1,11 | 0,2179 | |||||
| 3800 - 4740 | 1,64 | 0,1057 | |||||
| 4740 - 5680 | 2,16 | 0,0387 | |||||
| 5680 - 6620 | 2,69 | 0,011 | |||||
| 6620 - 7560 | 3,21 | 0,0024 | |||||
| 7560 - 8500 | 3,74 | 0,0004 | |||||
| 8500 - 9440 | 4,26 | 0,000016 | |||||
| Сумма |
- на основе фактических и теоретических накопленных частот рассчитываем разницу:
- рассчитываем критерий Колмогорова для определения соответствия эмпирического распределения нормальному. Для 5% уровня значимости находим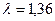 
, тогда 
. Как мы видим 
, следовательно, распределение не следует закону нормального распределения.
д) При исследовании распределения мы имеющиеся данные привели к виду групповой таблицы.
Проведя исследование, мы нашли среднее значение исследуемой величины и медиану, которая показывает середину совокупности. Также мы нашли среднее квадратичное отклонение, которое показывает, на сколько, в среднем, отклоняются данные от средней величины, и коэффициент вариации который переводит это значение в проценты. Для более наглядного представления распределения мы построили графики ряда (типа полигон и гистограмму).
|
|
|
Все значения вычислялись с учетом того, что ряд распределения вариационный. Для того, чтобы определить насколько распределение соответствует нормальному, мы провели его оценку на основе критерия Колмогорова.
Анализ многомерных рядов распределения.
ЗАДАЧА № 10
Исходные данные:
у – индекс снижения себестоимости продукции;
х1 – удельный вес рабочих в составе ППП;
х2 – непроизводственные расходы.
Таблица 6
| № п/п | y | x1 | x2 |
| 204,2 | 0,78 | 17,72 | |
| 209,6 | 0,75 | 18,39 | |
| 222,6 | 0,68 | 26,46 | |
| 236,7 | 0,7 | 22,37 | |
| 62,00 | 0,62 | 28,13 | |
| 53,1 | 0,76 | 17,55 | |
| 172,1 | 0,73 | 21,92 | |
| 56,5 | 0,71 | 19,52 | |
| 52,6 | 0,69 | 23,99 | |
| 46,6 | 0,73 | 21,76 | |
| 53,2 | 0,68 | 25,68 | |
| 30,1 | 0,74 | 18,13 | |
| 146,4 | 0,66 | 25,74 | |
| 18,1 | 0,72 | 21,21 | |
| 13,6 | 0,68 | 22,97 | |
| 89,8 | 0,77 | 16,38 | |
| 62,50 | 0,78 | 13,21 | |
| 46,3 | 0,81 | 14,48 | |
| 103,5 | 0,79 | 13,38 | |
| 73,30 | 0,77 | 13,69 | |
| 76,6 | 0,78 | 16,66 | |
| 73,00 | 0,72 | 15,06 | |
| 32,3 | 0,79 | 20,09 | |
| 199,6 | 0,77 | 15,98 | |
| 198,1 | 0,80 | 18,27 |
Строим групповую таблицу. Группировочный признак – у (индекс снижения себестоимости продукции). Величина интервала равна:
Количество групп найдем по формуле:
, и округляя вверх, получаем n = 6.
Величина интервала равна: 
. Округляя вверх, получаем i = 40
Получаем следующую групповую таблицу:
Таблица 7
| Интервал | Число предприятий | Средний удельный вес рабочих в составе ППП | Средние непроизводственные расходы |
| 5-45 | 0,73 | 20,6 | |
| 45-85 | 0,7 | 19,1 | |
| 85-125 | 0,78 | 14,88 | |
| 125-165 | 0,7 | 25,7 | |
| 165-205 | 0,8 | 18,5 | |
| 205-245 | 0,71 | 22,40 |
б) Графическое изображение зависимости можно дать в виде корреляционных полей.
Коэффициент корреляции можно найти по формуле:
Для его нахождения заполняем таблицу:
Таблица 8
| № п/п | y | x1 | x2 | 
| 
| 
| 
| 
| 
| 
| 
|
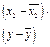
| 204,2 | 0,78 | 17,72 | 102,9 | 0,04 | -1,83 | 10589,2 | 0,0019 | 3,3 | 4,5 | -188,3 | |
| 209,6 | 0,75 | 18,39 | 108,3 | 0,01 | -1,16 | 11729,8 | 0,0002 | 1,3 | 1,5 | -125,6 | |
| 222,6 | 0,68 | 26,46 | 121,3 | -0,06 | 6,91 | 14714,7 | 0,0032 | 47,8 | -6,8 | 838,3 | |
| 236,7 | 0,70 | 22,37 | 135,4 | -0,04 | 2,82 | 18334,2 | 0,0013 | 8,0 | -4,9 | 381,9 | |
| 62,0 | 0,62 | 28,13 | -39,3 | -0,12 | 8,58 | 1544,2 | 0,0135 | 73,6 | 4,6 | -337,2 | |
| 53,1 | 0,76 | 17,55 | -48,2 | 0,02 | -2,00 | 2322,9 | 0,0006 | 4,0 | -1,1 | 96,4 | |
| 172,1 | 0,73 | 21,92 | 70,8 | -0,01 | 2,37 | 5013,2 | 0,0000 | 5,6 | -0,5 | 167,8 | |
| 56,5 | 0,71 | 19,52 | -44,8 | -0,03 | -0,03 | 2006,7 | 0,0007 | 0,0 | 1,2 | 1,3 | |
| 52,6 | 0,69 | 23,99 | -48,7 | -0,05 | 4,44 | 2371,3 | 0,0022 | 19,7 | 2,3 | -216,2 | |
| 46,6 | 0,73 | 21,76 | -54,7 | -0,01 | 2,21 | 2991,7 | 0,0000 | 4,9 | 0,4 | -120,9 | |
| 53,2 | 0,68 | 25,68 | -48,1 | -0,06 | 6,13 | 2313,2 | 0,0032 | 37,6 | 2,7 | -294,8 | |
| 30,1 | 0,74 | 18,13 | -71,2 | 0,00 | -1,42 | 5068,9 | 0,0000 | 2,0 | -0,3 | 101,1 | |
| 146,4 | 0,66 | 25,74 | 45,1 | -0,08 | 6,19 | 2034,4 | 0,0058 | 38,3 | -3,4 | 279,2 | |
| 18,1 | 0,72 | 21,21 | -83,2 | -0,02 | 1,66 | 6921,6 | 0,0003 | 2,8 | 1,4 | -138,1 | |
| 13,6 | 0,68 | 22,97 | -87,7 | -0,06 | 3,42 | 7690,6 | 0,0032 | 11,7 | 4,9 | -300,0 | |
| 89,8 | 0,77 | 16,38 | -11,5 | 0,03 | -3,17 | 132,2 | 0,0011 | 10,0 | -0,4 | 36,4 | |
| 62,5 | 0,78 | 13,21 | -38,8 | 0,04 | -6,34 | 1505,1 | 0,0019 | 40,2 | -1,7 | 246,0 | |
| 46,3 | 0,81 | 14,48 | -55,0 | 0,07 | -5,07 | 3024,6 | 0,0054 | 25,7 | -4,0 | 278,8 | |
| 103,5 | 0,79 | 13,38 | 2,2 | 0,05 | -6,17 | 4,9 | 0,0029 | 38,1 | 0,1 | -13,6 | |
| 73,3 | 0,77 | 13,69 | -28,0 | 0,03 | -5,86 | 783,8 | 0,0011 | 34,3 | -0,9 | 164,0 | |
| 76,6 | 0,78 | 16,66 | -24,7 | 0,04 | -2,89 | 609,9 | 0,0019 | 8,3 | -1,1 | 71,4 | |
| 73,0 | 0,72 | 15,06 | -28,3 | -0,02 | -4,49 | 800,7 | 0,0003 | 20,2 | 0,5 | 127,0 | |
| 32,3 | 0,79 | 20,09 | -69,0 | 0,05 | 0,54 | 4760,4 | 0,0029 | 0,3 | -3,7 | -37,3 | |
| 199,6 | 0,77 | 15,98 | 98,3 | 0,03 | -3,57 | 9663,7 | 0,0011 | 12,7 | 3,3 | -350,9 | |
| 198,1 | 0,80 | 18,27 | 96,8 | 0,06 | -1,28 | 9371,0 | 0,0040 | 1,6 | 6,2 | -123,9 | |
| Сумма | 2532,4 | 18,41 | 488,74 | 126302,6 | 0,0588 | 452,1 | 4,5 | 542,8 | |||
| Ср. знач. | 101,3 | 0,74 | 19,55 |
|
|
|
Вычисляем коэффициенты корреляции:
Между величинами х1 и y:
Коэффициент корреляции близок к нулю, следовательно связь между величиной y и величиной х1 отсутствует.
Между величинами х2 и y:
Коэффициент корреляции близок к нулю, следовательно связь между величиной y и величиной х2 отсутствует.
Оценим существенность коэффициентов корреляции при помощи t-критерия Стьюдента.
Для факторов y и x1:
Для факторов y и x2:
Сравниваем с табличным значением t-критерия Стьюдента, которое для доверительной вероятности 0,95 и количества степеней свободы 24 равно tтабл = 2,064.
Так как tтабл < tрас, то коэффициент корреляции rx1y считается несущественным.
Так как tтабл > tрас, то коэффициент корреляции rx2y считаются несущественным.
Для нахождения линейных уравнений связи заполним следующую таблицу:
Таблица 9
| № п/п | у | 
| 
| 
| 
| 
| 
| 
|
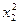
| 204,2 | 0,8 | 17,7 | 0,608 | 314,0 | 159,3 | 3618,4 | 13,82 | |
| 209,6 | 0,8 | 18,4 | 0,563 | 338,2 | 157,2 | 3854,5 | 13,79 | |
| 222,6 | 0,7 | 26,5 | 0,462 | 700,1 | 151,4 | 5890,0 | 17,99 | |
| 236,7 | 0,7 | 22,4 | 0,490 | 500,4 | 165,7 | 5295,0 | 15,66 | |
| 62,0 | 0,6 | 28,1 | 0,384 | 791,3 | 38,4 | 1744,1 | 17,44 | |
| 53,1 | 0,8 | 17,6 | 0,578 | 308,0 | 40,4 | 931,9 | 13,34 | |
| 172,1 | 0,7 | 21,9 | 0,533 | 480,5 | 125,6 | 3772,4 | 16,00 | |
| 56,5 | 0,7 | 19,5 | 0,504 | 381,0 | 40,1 | 1102,9 | 13,86 | |
| 52,6 | 0,7 | 24,0 | 0,476 | 575,5 | 36,3 | 1261,9 | 16,55 | |
| 46,6 | 0,7 | 21,8 | 0,533 | 473,5 | 34,0 | 1014,0 | 15,88 | |
| 53,2 | 0,7 | 25,7 | 0,462 | 659,5 | 36,2 | 1366,2 | 17,46 | |
| 30,1 | 0,7 | 18,1 | 0,548 | 328,7 | 22,3 | 545,7 | 13,42 | |
| 146,4 | 0,7 | 25,7 | 0,436 | 662,5 | 96,6 | 3768,3 | 16,99 | |
| 18,1 | 0,7 | 21,2 | 0,518 | 449,9 | 13,0 | 383,9 | 15,27 | |
| 13,6 | 0,7 | 23,0 | 0,462 | 527,6 | 9,2 | 312,4 | 15,62 | |
| 89,8 | 0,8 | 16,4 | 0,593 | 268,3 | 69,1 | 1470,9 | 12,61 | |
| 62,5 | 0,8 | 13,2 | 0,608 | 174,5 | 48,8 | 825,6 | 10,30 | |
| 46,3 | 0,8 | 14,5 | 0,656 | 209,7 | 37,5 | 670,4 | 11,73 | |
| 103,5 | 0,8 | 13,4 | 0,624 | 179,0 | 81,8 | 1384,8 | 10,57 | |
| 73,3 | 0,8 | 13,7 | 0,593 | 187,4 | 56,4 | 1003,5 | 10,54 | |
| 76,6 | 0,8 | 16,7 | 0,608 | 277,6 | 59,7 | 1276,2 | 12,99 | |
| 73,0 | 0,7 | 15,1 | 0,518 | 226,8 | 52,6 | 1099,4 | 10,84 | |
| 32,3 | 0,8 | 20,1 | 0,624 | 403,6 | 25,5 | 648,9 | 15,87 | |
| 199,6 | 0,8 | 16,0 | 0,593 | 255,4 | 153,7 | 3189,6 | 12,30 | |
| 198,1 | 0,8 | 18,3 | 0,640 | 333,8 | 158,5 | 3619,3 | 14,62 | |
| Сумма | 2532,4 | 18,41 | 488,74 | 13,616 | 10006,8 | 1869,3 | 50050,2 | 355,49 |
|
|
|
Находим простую линейную регрессию между х1 и у:
= а + bx1, где а и b – параметры, которые находятся из системы уравнений:
Решая систему, получаем: а = 39,45; b = 83,98, следовательно:
= 39,45 – 83,98x1
Находим простую линейную регрессию между х2 и у:
= а + bx2, где а и b – параметры, которые находятся из системы уравнений:
Решая систему, получаем: а = 77,83; b = 1,2, следовательно:
= 77,83 + 1,2x2
Находим множественную линейную регрессию между х1, х2 и у:
= а + bx1 + сх2, где а, b и с – параметры, которые находятся из системы уравнений:
Решая систему, получаем: а = -497,7; b = 620,6; с = 7,26, следовательно:
= -214,8 + 46x1 + 410,7х2
г) Для того, чтобы оценить существенность параметров уравнения воспользуемся формулами:
, 
,
, где 
- остаточная дисперсия
Для 5% уровня значимости tтабл = 2,069.
Заполним следующую таблицу:
Таблица 10
| № п/п | у |
|
| 
| 
| 
| 
| 
| 
| 
| 
|
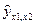
| 204,2 | 0,78 | 17,72 | 0,0000 | 0,0039 | 101,253 | 125,4 | 127,1 | 10598,1 | 6209,4 | 5944,4 | |
| 209,6 | 0,75 | 18,39 | 0,0151 | 0,0008 | 100,737 | 90,57 | 95,657 | 11851,2 | 14168,1 | 12983,0 | |
| 222,6 | 0,68 | 26,46 | 0,0151 | 0,0027 | 100,737 | 121,53 | 128,513 | 14850,6 | 10215,1 | 8852,4 | |
| 236,7 | 0,70 | 22,37 | 0,0045 | 0,0005 | 101,554 | 109,92 | 107,452 | 18264,4 | 16073,2 | 16705,0 | |
| 62,0 | 0,62 | 28,13 | 0,0000 | 0,0018 | 101,253 | 117,66 | 118,886 | 1540,8 | 3098,0 | 3236,0 | |
| 53,1 | 0,76 | 17,55 | 0,0496 | 0,0136 | 100,307 | 56,127 | 63,7047 | 2228,5 | 9,2 | 112,5 | |
| 172,1 | 0,73 | 21,92 | 0,0053 | 0,0002 | 100,952 | 106,05 | 109,785 | 5062,0 | 4362,6 | 3883,2 | |
| 56,5 | 0,71 | 19,52 | 0,0033 | 0,0000 | 101,511 | 102,18 | 99,698 | 2026,0 | 2086,7 | 1866,1 | |
| 52,6 | 0,69 | 23,99 | 0,0007 | 0,0077 | 101,382 | 67,35 | 64,115 | 2379,7 | 217,6 | 132,6 | |
| 46,6 | 0,73 | 21,76 | 0,0003 | 0,0060 | 101,339 | 71,22 | 68,682 | 2996,4 | 606,1 | 487,6 | |
| 53,2 | 0,68 | 25,68 | 0,0000 | 0,0105 | 101,253 | 140,88 | 143,528 | 2309,1 | 7687,8 | 8159,1 | |
| 30,1 | 0,74 | 18,13 | 0,0769 | 0,0000 | 102,457 | 102,18 | 89,578 | 5235,5 | 5195,5 | 3537,6 | |
| 146,4 | 0,66 | 25,74 | 0,0758 | 0,0002 | 102,448 | 106,05 | 93,777 | 1931,7 | 1628,1 | 2769,2 | |
| 18,1 | 0,72 | 21,21 | 0,0115 | 0,0002 | 101,726 | 106,05 | 101,505 | 6993,3 | 7735,2 | 6956,4 | |
| 13,6 | 0,68 | 22,97 | 0,0014 | 0,0027 | 101,425 | 121,53 | 121,153 | 7713,2 | 11648,9 | 11567,6 | |
| 89,8 | 0,77 | 16,38 | 0,0005 | 0,0003 | 101,167 | 94,44 | 95,164 | 129,2 | 21,5 | 28,8 | |
| 62,5 | 0,78 | 13,21 | 0,0086 | 0,0014 | 100,866 | 86,7 | 90,17 | 1471,9 | 585,6 | 765,6 | |
| 46,3 | 0,81 | 14,48 | 0,0022 | 0,0060 | 101,468 | 71,22 | 67,302 | 3043,5 | 621,0 | 441,1 | |
| 103,5 | 0,79 | 13,38 | 0,0005 | 0,0023 | 101,167 | 82,83 | 82,843 | 5,4 | 427,2 | 426,7 | |
| 73,3 | 0,77 | 13,69 | 0,0176 | 0,0008 | 100,694 | 90,57 | 96,117 | 750,4 | 298,3 | 520,6 | |
| 76,6 | 0,78 | 16,66 | 0,0496 | 0,0001 | 100,307 | 98,31 | 108,471 | 562,0 | 471,3 | 1015,8 | |
| 73,0 | 0,72 | 15,06 | 0,0005 | 0,0077 | 101,167 | 67,35 | 66,415 | 792,8 | 32,0 | 43,5 | |
| 32,3 | 0,79 | 20,09 | 0,0068 | 0,0068 | 100,909 | 133,14 | 138,994 | 4707,2 | 10168,7 | 11383,6 | |
| 199,6 | 0,77 | 15,98 | 0,0162 | 0,0039 | 101,812 | 125,4 | 121,12 | 9562,5 | 5505,6 | 6159,1 | |
| 198,1 | 0,80 | 18,27 | 0,0115 | 0,0085 | 101,726 | 137,01 | 134,361 | 9287,9 | 3732,0 | 4062,7 | |
| Σ | 18,4 | 488,7 | 0,37 | 0,09 | 126293,6 | 112805,0 | 112040,2 | ||||
| Ср. | 101,3 | 0,74 | 19,55 |
Оцениваем существенность параметров уравнения для регрессии у(х1):
tрасч > tтабл, следовательно параметр существенен.
tрасч < tтабл, следовательно параметр несущественен.
Оцениваем существенность параметров уравнения для регрессии у(х2):
tрасч > tтабл, следовательно параметр существенен.
tрасч < tтабл, следовательно параметр несущественен.
Оцениваем существенность параметров уравнения для регрессии у(х1,х2):
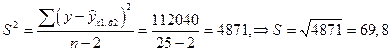
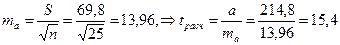
tрасч > tтабл, следовательно параметр существенен.
tрасч < tтабл, следовательно параметр несущественен.
tрасч < tтабл, следовательно параметр несущественен.
д) Ошибка аппроксимации находится по формуле:
Для нахождения ошибки аппроксимации заполним таблицу:
Таблица 11
| № п/п | у | 
| 
| 
|
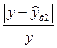
| 204,2 | 0,50 | 0,39 | 0,38 | |
| 209,6 | 0,52 | 0,57 | 0,54 | |
| 222,6 | 0,55 | 0,45 | 0,42 | |
| 236,7 | 0,57 | 0,54 | 0,55 | |
| 62,0 | 0,63 | 0,90 | 0,92 | |
| 53,1 | 0,89 | 0,06 | 0,20 | |
| 172,1 | 0,41 | 0,38 | 0,36 | |
| 56,5 | 0,80 | 0,81 | 0,76 | |
| 52,6 | 0,93 | 0,28 | 0,22 | |
| 46,6 | 1,17 | 0,53 | 0,47 | |
| 53,2 | 0,90 | 1,65 | 1,70 | |
| 30,1 | 2,40 | 2,39 | 1,98 | |
| 146,4 | 0,30 | 0,28 | 0,36 | |
| 18,1 | 4,62 | 4,86 | 4,61 | |
| 13,6 | 6,46 | 7,94 | 7,91 | |
| 89,8 | 0,13 | 0,05 | 0,06 | |
| 62,5 | 0,61 | 0,39 | 0,44 | |
| 46,3 | 1,19 | 0,54 | 0,45 | |
| 103,5 | 0,02 | 0,20 | 0,20 | |
| 73,3 | 0,37 | 0,24 | 0,31 | |
| 76,6 | 0,31 | 0,28 | 0,42 | |
| 73,0 | 0,39 | 0,08 | 0,09 | |
| 32,3 | 2,12 | 3,12 | 3,30 | |
| 199,6 | 0,49 | 0,37 | 0,39 | |
| 198,1 | 0,49 | 0,31 | 0,32 | |
| Σ | 2532,4 | 27,8 | 27,6 | 27,4 |
Находим ошибку аппроксимации уравнения для регрессии у(х1):
Находим ошибку аппроксимации уравнения для регрессии у(х2):
Находим ошибку аппроксимации уравнения для регрессии у(х1,х2):
е) На первой стадии нашего анализа (построение групповой таблицы) мы пришли к выводу, что заметной зависимости между величиной у и величинами х1 и х2 нет. При увеличении у величина х2 принимает совершенно различные значения, между которыми невозможно выявить какой-либо тенденции. А величина х2 хаотично изменяется в пределах от 0,6 до 0,8. Из групповой таблицы также можно сделать вывод, что индекс снижения себестоимости почти у половины предприятий находится в интервале 45 – 85. Построив корреляционные поля, мы наглядно увидели, что какой либо заметной зависимости нет.
Мы нашли линейные уравнения связи (простую и множественную регрессии). Однако, оценив существенность параметров, мы пришли к выводу, что только один из параметров в каждом уравнении является существенным. А большое значение ошибки аппроксимации говорит о том, что эти уравнения нельзя применять в дальнейшем анализе.
|
|
|
