Различные способы представления синусоидального тока

Основные понятия и определения

 

Однофазным переменным током называется ток, изменяющийся по закону синуса:

i = I_m·sin ωt

где i - мгновенное значение тока; I_m – амплитудное (максимальное) значение тока

 

Преимуществами переменного тока перед постоянным является простота передачи его на дальние расстояния с использованием трансформаторных подстанций, простота устройства генераторов переменного тока, простота и надежность в эксплуатации двигателей переменного тока.

Величина ЭДС электромагнитной индукции зависит от магнит­ной индукции В, активной длины проводника l, скорости пересе­чения проводником магнитных силовых линий V и синуса угла  между направлением вектора магнитной индукции и вектора скорости. ЭДС электромагнитной индукции определяется по формуле:

 

e = B·l·V·sina.

 

Рассмотрим зависимость Э Д С электромагнитной индук­ции от a:

 

a = 0 e = 0

a = 90⁰ e = max, e = B·l·V·sin 90⁰ = B·l·V = E _m

a = 180⁰ e = 0

a = 270⁰ e = -max, e = B·l·V·sin 270⁰ =- B·l·V = - E _m

a = 360⁰ e = 0

 

С учетом обозначения E _m = B·l·V формула определения ЭДС электромагнитной индукции запишется следующим образом:

 

e = E _m sin a

 

Ток, изменяющийся по закону синуса определится по формуле:

 

i = I_m·sin a

 

Угловая скорость w равна углу поворота рамки в единицу времени:

 

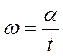или

 

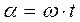
С учетом этого соотношения определим основные понятия пе­ременного тока, используя кривую изменения тока (рисунок 2.1).

 

i = I_m·sin (wt + y),

 

где i - мгновенное значение тока; I_m -максимальное значение тока; (wt + y) - фаза, характеризующая состояние колебаний в данный момент времени t; y - начальная фаза.

 

 

Рисунок 2.1

 

Период Т - это время, в течение которого происходит пол­ное изменение тока, измеряется в секундах.

Величина, обратная периоду, называется частотой f, изме­ряется в герцах.

Вместо единицы измерения угла в градусах можно пользо­ваться единицей измерения в радианах. Радианом называется угол, дуга которого равна радиусу. Так как длина окружности C = 2pR, то полному углу 360⁰ соответствует 2pR / R радиан. 360⁰ соответствует периоду Т. Используя это соотношение, найдем формулу, связывающую угловую частоту w c циклической f, а именно:

 

w = a / t = 2p / T = 2p f

 

Среднее значение синусоидального тока определяется за полпериода:

 

 

Среднее значение ЭДС и напряжения определяется аналогич­но:

 

 

Действующее значение синусоидального тока принято оцени­вать тепловым эффектом. Для оценки теплового действия, произ­водимого переменным током, необходимо сравнить его с тепловым действием постоянного тока. Для этого по одному и тому же соп­ротивлению R пропустим постоянный ток, затем переменный ток (рисунок 2.2 а, б) и приравниваем количество тепла, выделяемое эти­ми токами в течение времени, равного периоду Т. Количество тепла определяется по формуле Джоуля - Ленца.

 

 

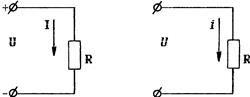
а) б)

 

Рисунок 2.2

 

Для постоянного тока количество тепла определяется по следующей

формуле:

Q _ = R · I ²· t = R · I ²· T,

 

где Q _- количество тепла, выделяемое на сопротивлении R; I - ток, протекаю-

щий по сопротивлению R; t - время, в течение которого пропускается ток по сопро­тивлению R.

 

Для переменного тока количество тепла (Q) определяется по следующей формуле:

 

 

Так как Q_ = Q_~, то

 

 

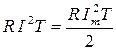
отсюда ,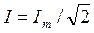

 

где I - действующее значение переменного тока.

 

 

Различные способы представления синусоидального тока

Существуют три основных способа представления синусоидального тока: тригонометрическое, графическое, изображение на комплексной плоскости.

1. Тригонометрический способ представления:

 

i = I_m·sin wt

 

2. Графический способ представления (рисунок 2.3):

 

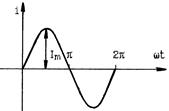
Рисунок 2.3

 

3. Изображение на комплексной плоскости:

С целью единообразия векторы синусоидального тока на комплексной плоскости принято изображать для момента времени wt = 0.

Ток i = I _m· sin (w · t ± y)в показательной форме с ис­пользованием формулы Эйлера будет определяться следующим обра­зом:

 

I _m = I _m e^{j(w t±y)}

 

или для wt = 0 I _m = I _m e^{j(±y )},

 

где I _m - комплексное значение переменного тока; I_m - модуль; - мнимая единица.

 

Рассмотрим примеры записи комплексных величин для тока:

тригонометрическая форма записи:

 

i = 8 sin (wt - 20^o)

комплексная форма записи:

I _m =

На комплексной плоскости изображение вектора переменного тока показано на рисунке 2.4.

 

 

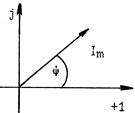
Рисунок 2.4

 

Совокупность векторов на комплексной плоскости, изобража­ющих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе (угол y), называется вектор­ной диаграммой. Одновременный поворот всех векторов на один и тот же угол не изменит их взаимного расположения, исходя из этого, можно ввести понятие исходного вектора.

Исходным векто­ром называется вектор, совпадающий с осью +1 комплексной плос­кости.

Поделиться:

Воспользуйтесь поиском по сайту: