 |
Линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель
|
|
|
|
линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель
связи между результативным признаком и остальными, включенными в модель
нелинейной зависимости между двумя признаками
Парный коэффициент корреляции может принимать значения
от 0 до 1
от -1 до 0
от -1 до +1
Коэффициент детерминации может принимать значения
От 0 до 1
от -1 до 0
от -1 до +1
В результате проведения регрессионного анализа получают функцию, описывающую... показателей
Взаимосвязь
соотношение
структуру
темпы роста
темпы прироста
Прямолинейная связь между факторами исследуется с помощью уравнения регрессии
+ 
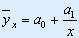
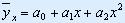
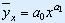
С помощью коэффициентов Спирмена и Чупрова устанавливается связь между признаками:
только количественными
только качественными
Количественными и качественными
Тема 7. Статистическое изучение динамики
Ряд динамики характеризует:
Изменение явления во времени
распределение единиц совокупности по какому-либо признаку
распределение единиц совокупности по территории страны
Уровни ряда – это:
ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение явления во времени
Показатели, числовые значения которых составляют динамический ряд
моменты или периоды времени, к которым относятся числовые значения признака
Время в статистике – это:
ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение явления во времени
показатели, числовые значения которых составляют динамический ряд
|
|
|
Моменты или периоды времени, к которым относятся уровни ряда
Моментным называют:
Ряд динамики, уровни которого характеризуют состояние явления на отдельные даты
ряд динамики, уровни которого характеризуют явления за конкретный период времени
Интервальным называют:
ряд динамики, уровни которого характеризуют состояние явления на отдельные даты
Ряд динамики, уровни которого характеризуют явления за конкретный период времени
Для интервальных рядов динамики с равностоящими во времени уровнями расчет средней производится по формуле:
Простой средней арифметической
взвешенной средней арифметической
средней хронологической
Для интервальных рядов динамики с не равностоящими во времени уровнями расчет средней производится по формуле:
простой средней арифметической
Взвешенной средней арифметической
средней хронологической
Для моментных рядов динамики с равностоящими во времени уровнями расчет средней производится по формуле:
взвешенной средней арифметической
Средней хронологической
средней скользящей взвешенной
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень:
базисным
Отчетным
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть уровень
с которым производится сравнение:
Базисным
отчетным
Коэффициент роста показывает:
Во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение
на сколько процентов сравниваемый уровень больше уровня, принятого за базу сравнения
во сколько раз в среднем за единицу времени изменяется уровень ряда динамики
Темп роста показывает:
во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение
|
|
|
|
|
|


