 |
По дисциплине: «Теория узкополосных шумов в радиоэлектронных устройствах и системах»
|
|
|
|
Министерство науки и высшего образования
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ»
(КНИТУ-КАИ)
Институт радиоэлектроники и телекоммуникаций (ИРЭТ)
Кафедра радиоэлектронных и квантовых устройств (РЭКУ)
Отчет лабораторной работы № 3
На тему: «Детектирование узкополосного шума,, полученного в ЛР №1»
По дисциплине: «Теория узкополосных шумов в радиоэлектронных устройствах и системах»
Направление 11.04.02 Инфокоммуникационные технологии и системы связи
Выполнил:
студент гр. 5296 Галиев И.И.
Проверил: профессор, д.т.н.
Ильин Александр Германович
Казань, 2019 год
Задание.
Произвести детектирование узкополосного шума, полученного в ходе выполнения лабораторной работе №1.
Теория.
Детектирование (от лат. detectio – открытие, обнаружение), преобразование электрических колебаний, в результате которого получаются колебания более низкой частоты или постоянный ток.
Модулированное по амплитуде колебание представляет собой в простейшем случае совокупность трёх высоких частот w, w + W и w – W, где w – высокая несущая частота, W – низкая частота модуляции. Т. к. сигнала частоты W нет в модулированном колебании, то Д. обязательно связано с преобразованием частоты. Электрические колебания подводятся к устройству (детектору), которое проводит ток только в одном направлении. При этом колебания превратятся в ряд импульсов тока одного знака. Если амплитуда детектируемых колебаний постоянна, то на выходе детектора импульсы тока имеют постоянную высоту (рисунок 1).
|
|
|
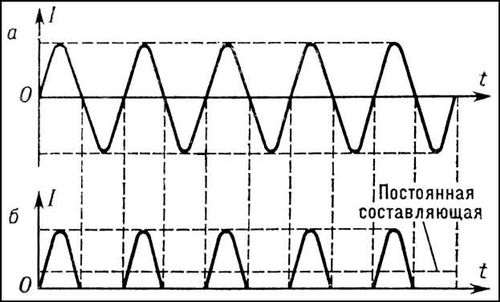
Рисунок 1 – На входе детектора колебания с постоянной амплитудой (а); на выходе детектора импульсы тока I одинаковой высоты (б). Детектор регистрирует постоянную составляющую тока.
Если амплитуда колебаний на входе детектора изменяется, то высота импульсов тока становится различной. Огибающая импульсов при этом повторяет закон изменения амплитуды подводимых к детектору модулированных колебаний (рисунок 2).

Рисунок 2 – а – колебания с амплитудной модуляцией на входе детектора; б – импульсы тока на его выходе. Детектор регистрирует переменный ток низкой частоты (нижняя пунктирная линия).
Если колебания выпрямляются лишь частично, т. е. ток через детектор течёт в обоих направлениях, но электропроводность детектора различна, то Д. также происходит. Т. о., для Д. можно использовать любое устройство с различной электропроводностью в различных направлениях, например диод. Спектр частот тока, прошедшего через диод, значительно богаче спектра исходного модулированного колебания. Он содержит постоянную составляющую, колебание частоты W, а также составляющие с частотами w, 2w, Зw и т.д. Для выделения сигнала частоты W ток диода пропускается через линейный фильтр, обладающий высоким сопротивлением на частоте W и малым сопротивлением на частотах w, 2w и т.д. Простейший фильтр состоит из сопротивления R и ёмкости С, величина которых определяется условиями wRC >> 1 и WRC << 1. Напряжение на выходе этого фильтра имеет частоту W и амплитуду, пропорциональную глубине модуляции входного колебания высокой частоты.
Рассмотренный выше детектор с кусочно-линейной зависимостью тока от напряжения (рисунок 3, б), называется линейным, воспроизводит практически без искажений колебание низкой частоты W, которым модулировался входной сигнал (рис. 3, в).
|
|
|
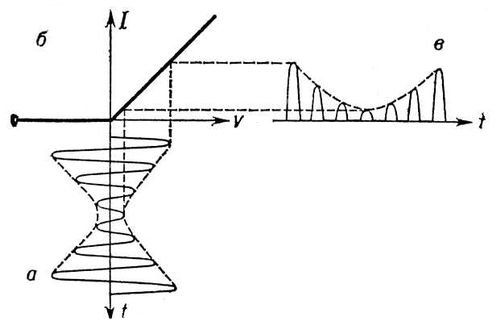
Рисунок 3 – а – амплитудно-модулированное колебание на входе детектора; б – вольтамперная характеристика детектора; в – колебания тока на выходе детектора.
Выполнение работы.
Запишем код:
Сначала сформируем сигнал:
Tm=5;% Длина сигнала (с)
Fd=512;% Частота дискретизации (Гц)
Ak=0.5;% Постоянная составляющая
A1=1;% Амплитуда первой синусоиды
A2=0.7;% Амплитуда второй синусоиды
F1=13;% Частота первой синусоиды (Гц)
F2=42;% Частота второй синусоиды (Гц)
Phi1=0;% Начальная фаза первой синусоиды (Градусов)
Phi2=37;% Начальная фаза второй синусоиды (Градусов)
An=3*A1;% Дисперсия шума
FftL=1024;% Количество линий Фурье спектра
%% Генерация рабочих массивов
T=0:1/Fd:Tm;% Массив отсчетов времени
Noise=An*randn(1,length(T));% Массив случайного шума
Signal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% Массив сигнала (смесь 2х синусоид и постоянной составляющей)
Сформируем спектр сигнала:
FftS=abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала
FftS=2*FftS./FftL;% Нормировка спектра по амплитуде
FftS(1)=FftS(1)/2;% Нормировка постоянной составляющей в спектре
FftSh=abs(fft(Signal+Noise,FftL));% Амплитуды преобразования Фурье смеси сигнал+шум
FftSh=2*FftSh./FftL;% Нормировка спектра по амплитуде
FftSh(1)=FftSh(1)/2;% Нормировка постоянной составляющей в спектре
Демодуляция АМ методом синхронного детектирования:
y = s_AM.* cos(omega0*t); % умножение на опорное колебание
[b, a] = butter(5, 2*OMEGA/pi/Fs); % сглаживающий ФНЧ
z = filtfilt(b, a, y); % пропускаем сигнал через ФНЧ
Построим графики:
subplot(2,1,1);% Выбор области окна для построения
plot(T,Signal);% Построение сигнала
title('Сигнал');% Подпись графика
xlabel('Время (с)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(T,Signal+Noise);% Построение смеси сигнал+шум
title('Сигнал+шум');% Подпись графика
xlabel('Время (с)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
F=0:Fd/FftL:Fd/2-1/FftL;% Массив частот вычисляемого спектра Фурье
figure% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
plot(F,FftS(1:length(F)));% Построение спектра Фурье сигнала
title('Спектр сигнала');% Подпись графика
xlabel('Частота (Гц)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(F,FftSh(1:length(F)));% Построение спектра Фурье сигнала
|
|
|
title('Спектр сигнала');% Подпись графика
xlabel('Частота (Гц)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
figure
plot(t, s_AM, '--', t, z);
title('Демодуляция АМ');
legend('АМ-сигнал', 'Демодулированный сигнал');
hold off
В результате выполнения получим графики:

Рисунок 1 – Информационный сигнал
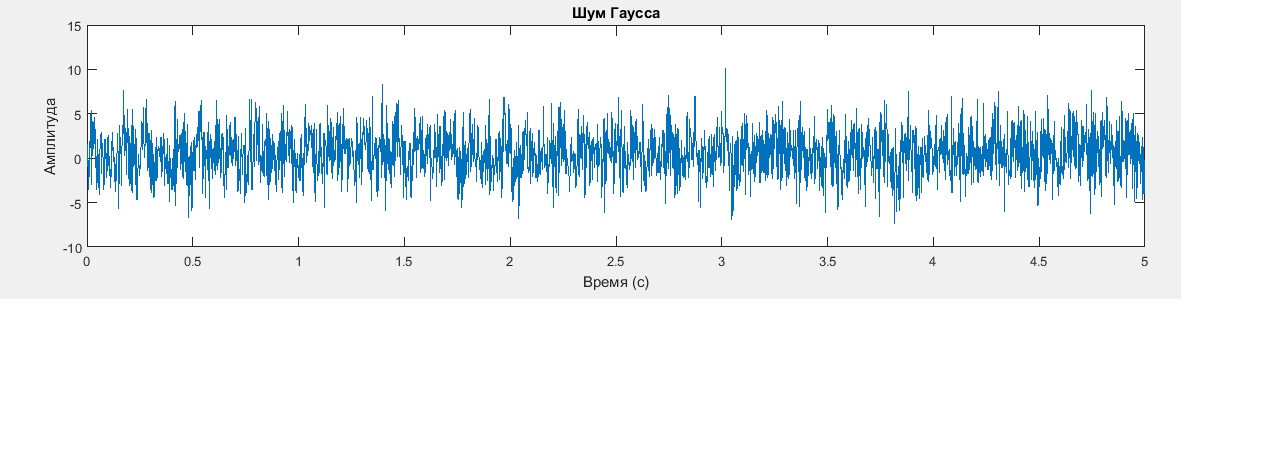
Рисунок 2 – Шум Гаусса
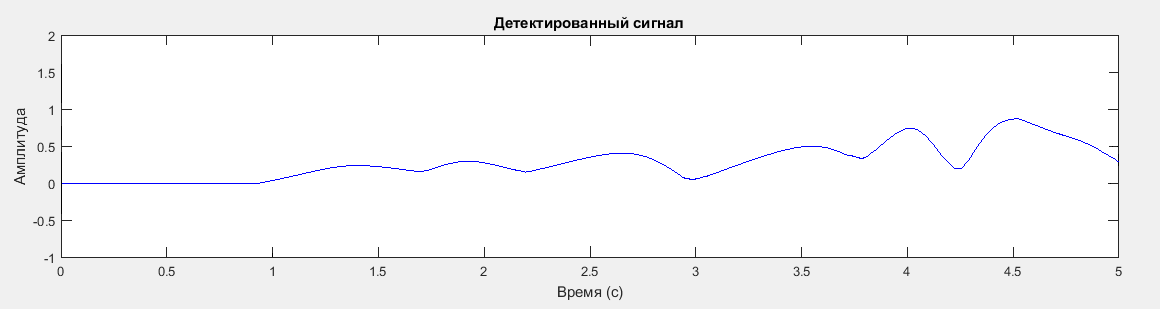
Рисунок 3 – Детектированный сигнал
|
|
|


