 |
Расчёт режима обжатий полосовой стали
|
|
|
|
Для расчёта режимов обжатия полосовой стали применяют несколько методик. Наиболее известные из них это расчёт по предельным условиям захвата, по условиям полного использования мощности электродвигателей главных приводов и по коэффициентам высотной деформации, которая на основании практического опыта разработана известным калибровщиком Н.В.Литовченко.
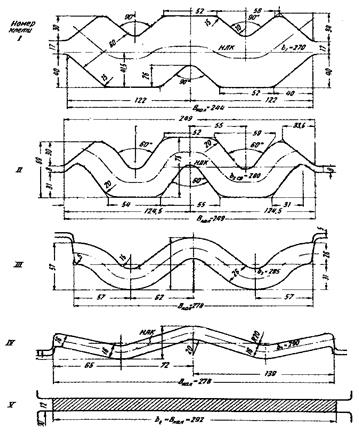
Рис.15.7 - Схема прокатки полосовой стали с изогнутой стенкой)
:
Система калибров для прокатки широких полос – включает только пластовые калибры, а при прокатке узких полос с острыми кромками – чередование пластовых и ребровых калибров. Соотношение размеров исходной заготовки и готовой полосы приведено на рисунке 15.8. Перед началом расчёта необходимо проверить

Рис.15.8 – Соотношение размеров исходного квадрата и готового профиля
условия захвата и прочность валков. С учётом уменьшения диаметра валков при переточках и для обеспечения устойчивости захвата максимальное обжатие можно определить по формуле:
∆hмакс = 0,77 f 2R, (11.1)
а среднее:
∆hсред ≈ 0,5 ∆hмакс. (11.2)
При прокатке полосовой стали коэффициенты деформации η близки к коэффициентам вытяжки µ. В зависимости от характеристик оборудования и возможностей сортового стана, коэффициенты высотной деформации выбирают в соответствии с рекомендациями, приведенными в таблице 15.2
Таблица 15.2 - Коэффициенты высотной деформации полосовой стали, η
| № прохода против хода прокатки | Коэффициенты высотной деформации при обжатии полок | |||
| очень высокие | высокие | средние | пониженные | |
| 1,35 – 1,4 | 1,28 – 1,3 | 1,2 – 1,25 | 1,1 – 1,15 | |
| 1,55 – 1,6 | 1,45 – 1,5 | 1,35 – 1,4 | 1,15 – 1,2 | |
| 1,75 – 1,8 | 1,6 – 1,7 | 1,45 – 1,5 | 1,2 -,25 | |
| 1,95 – 1,2 | 1,75 – 1,8 | 1,55 – 1,6 | 1,25 – 1,3 | |
| 1,95 – 1,2 | 1,75 – 1,2 | 1,55 – 1,6 | 1,25 – 1,3 | |
| - | 1,75 – 1,9 | 1,65 | 1,3 | |
| - | 1,9 | 1,65 | 1,3 | |
| - | 1,9 | 1,65 | 1,3 |
|
|
|
При обжатии полос по ширине в ребровых проходах, чем ближе калибр к чистовому калибру, чем тоньше полоса и больше отношение её ширины к толщине, тем меньше принимается величина абсолютного высотного обжатия. По условиям деформации величину высотного обжатия принимают в пределах:
∆h ≤ (0,5 – 1,0)∆hмакс или η = 1,05 ÷ 1,07,
при чём для предчистового ребрового калибра принимают обжатие - 0,5∆ h макс, а для остальных калибров 1,0∆ h макс. Количество ребровых проходов определяют в зависимости от технологических особенностей конкретного стана. При построении ребровых калибров (рис.15.9) руководствуются соотношениями:

а б)
Рис.15.9 – Ребровый калибр для прокатки полосовой стали, расположенный в:
а) в горизонтальных валках; б) в вертикальных валках.
Ширина калибра у дна: b k = (0,98 ¸ 1,06)b1;
где b1 - толщина задаваемой полосы.
Уклон составляет (5…10)% или: tg y = 0,05…0,10;
Величина прогиба дна калибра: ∆ = 0,5 ¸ 1,0 мм;
Глубина ручья (hp) определяется шириной прокатываемой полосы;
Зазор между буртами: S (t) ≈ 0,015 Д;
Радиус закругления у буртов: R ≈ 2 ¸ 10 мм.
Режим обжатий полосовой стали рассчитывают против хода прокатки, а размеры исходной заготовки определяются после расчёта калибровки. На рисунке 11.10 приведена схема прокатки полосовых профилей смежных размеров.

Рис.11.10 – Схема прокатки полос смежных сечений на крупносортном стане 500
а - 10×200 и 12×200 мм; б - 10×180 и 10×170 мм; в - 14×180 мм; г - 30×180 и 20×180 мм.
Пример. Рассчитать по коэффициентам высотной деформации режим обжатий полосы сечением 18×160 мм в клетях крупносортного девятиклетьевого стана 500. Диаметры валков: клетей 1 — IV - 630 мм, клетей V – IX- 540 мм. Материал валков: клетей 1—IV — сталь, клетей V —IX — чугун, скорость прокатки в 9 клети 9м/с. Режим обжатий примем средний. Исходя из расположения оборудования на стане, возможностей кантовки раската принимаем расположение ребровых калибров в клетях VIII и V, а в остальных клетях - валки с гладкой бочкой. На основании практических данных принимаем распределение температур и коэффициентов деформации при прокатке полосы по клетям (табл.15.3).
|
|
|
Таблица 15.3 – Распределение температур раската по клетям
| Клеть № | Исходная заготовка | |||||||||
| t, ºС | ||||||||||
| η | 1,25 | 1,05 | 1,4 | 1,5 | 1,132 | 1,6 | 1,65 | 1,65 |
Расчёт ведем против хода прокатки. Уширение рассчитываем по формуле Б.Бахтинова или Э.Зибеля:

 ;
; 
Клеть IX. По таблице 15.2 принимаем среднее значение коэффициента деформации (столбец 4) η 9 = 1;25; D9 = 540 мм. Размеры поперечного сечения профиля с учётом температурного расширения:
b9 = 1.013×160 ≈ 162,0 мм, h9 = 1.013×18 ≈ 18.25 мм.
Площадь поперечного сечения полосы: после чистовой клети:
F9 = h9 × b9= 18,25 ×162 ≈ 2960 мм2;
Обжатие в клети IX:
∆h9 = H8 - h9 = 22.8 – 18.25 = 4.45 мм.
Высота полосы, входящей в девятый калибр:
H9 = b 8 = h9×η9 = 18.25 ×1.25 = 22.8 мм.
Уширение в клети IX:
 .
.
Ширина полосы, входящей в девятый калибр:
В 9 = h 8 = b9 - ∆b9 = 162 – 2,5 = 159,5 мм.
Клеть VIII. Ребровой проход. Так как в восьмой клети принят ребровой проход, то перед проходом производят кантовку раската на 90º. С учётом этого, h8 = b8 = 159,5 мм, а b8 = H8 = 22,8 мм. Диаметр валков по буртам D 8 = 540 мм. Катающий диаметр с учётом зазора между валками 10 мм:
DК8 = D8 + S - h8 = 540 + 10 — 159,5 = 390,5 мм.
Принимаем: D K8 = 390 мм и коэффициент деформации высоты раската
η 8 = 1,05, тогда высота полосы, входящей в ребровой калибр
H8 = h8×η8 = 159,5,8 × 1.0,5 = 167.5 мм,
/обжатие в ребровом калибре составит:
∆h8 = H8 – h8 = 167,5 – 159,5 = 8 мм.
Так как по сравнению с шириной полосы обжатие в ребровом проходе очень маленькое (Ԑ = (∆h8 / H8)×100 = 4, 77%), уширением раската пренебрегают. Окончательные размеры входящей полосы:
H8 = b7 = 167,5 мм, В8 = h7 = 22,8 мм.
Площадь поперечного сечения полосы после восьмой клети: Площадь поперечного сечения полосы в восьмом калибре:
F8 = h8×b 8 = 22,8 × 159,5 ≈ 3640 мм2.
Коэффициент вытяжки поперечного сечения раската в девятой клети:
|
|
|
µ 9 = F8 / F9 = 3640 / 2960 ≈ 1,23.
Обжатие в ребровом калибре можно найти по максимальному обжатию.
При температуре раската t = 935ºС (табл.15.3), коэффициент трения составит:
f8 = k1 k2 k3 (1,05 – 0,0005t) = (1,05-0,0005-935)×0,8 = 0,465.
По (11.1) определим максимально возможное обжатие в ребровом проходе клети VIII:
∆hср = 0,5×0,77f 2R = 0,77×0,4852× 195 = 16,2 мм.
∆h8 < ∆h8 сред или 8 < 16,2 мм.
Принятый коэффициент высотной деформации в ребровом проходе клети № 8 удовлетворяет расчётной величине обжатия.
Клеть VII. h7 =22,8 мм; b7 = 167,5 мм; D7 = 540 мм; η7 = 1,4.
Высота входящей полосы
H7 = h7 × η7 = 22,8×1,4 = 32 мм.
Обжатие
∆h7 = H7 – h7 = 32 – 22,8 = 9,.2 мм.
Уширение

Ширина входящей полосы
В7 = b7 - ∆b7 = 167,5 – 5 = 162,5 мм.
Площадь поперечного сечения после седьмой клети
F7 = H7×b7= 22,8 × 167,5 ≈ 3820 мм2.
Коэффициент вытяжки поперечного сечения раската в восьмой клети:
µ 8 = F7 / F8 = 3820 / 3640 ≈1,05.
Клеть VI. h6 =32 мм; b6 = 162,5 мм; D6 = 540 мм; η6 = 1,5.
Высота входящей полосы
H6 = h6 × η6 = 32×1,5 = 48мм.
Обжатие
∆h6 = H6 – h6 = 48 – 32 = 16 мм.
Уширение

Ширина входящей полосы
В6 = b6 - ∆b6 = 162,5 – 7,7 = 154,8 мм.
Площадь поперечного сечения после седьмой клети
F6 = h6×b6= 32 × 162,5 ≈ 5200 мм2.
Коэффициент вытяжки поперечного сечения раската в седьмой клети:
µ 7 = F6 / F7 = 5200 / 3820 ≈1,36.
Клеть V. Ребровой проход. Диаметр бочки валка D = 540 мм. Катающий диаметр при зазоре 10 мм.
Dк5 = D+S–В6=540+10–154,8=395,2 мм,
h5 = В 6 = 154,8 мм, аb5 = H6 = 48 мм.
Принимаем Dк5 = 395 мм и коэффициент деформации высоты раската
η 5 = 1,132, тогда высота полосы, входящей в ребровой калибр
H5 = h5×η5 = 154,8 × 1.132
Тогда: h5 =154,8 мм; b5 = 48 мм; t = 1035ºС,
f5 = k1 k2 k3 (1,05 – 0,0005t) = (1,05-0,0005-1035)×0,8 = 0,425.
Обжатие
∆h 5 = 0,57×0,77f 25Rк 5 = 0,75×0,77×0,4252×197,5 = 20,5 мм.
H5 = h5 + ∆h 5 = 154,8 + 20,5 = 175,3 мм.
Коэффициент деформации
η = 175,3 / 154,8 ≈ 1,132.
Уширение

Ширина входящей полосы
В5 = b5 - ∆b5 = 48 – 2,5 = 45,5 мм.
Площадь поперечного сечения раската после пятой клети
F5 = H5×b5= 154,8 × 48 ≈ 7440 мм2.
Коэффициент вытяжки поперечного сечения раската в шестой клети:
µ 6 = F5 / F6 = 7440 / 5200 ≈1,43.
Клеть 1V. h4 = В5 = 45,5 мм; b4 = Н5 =175,3 мм; D4 = 630 мм; η4 = 1,6.
|
|
|
Высота входящей полосы
Н4 = h4×η4 = 45,4×1,6 ≈ 73 мм.
Обжатие
∆h4 = H4 – h4 = 73 – 45,5 = 27,5 мм.
Уширение

Ширина входящей полосы
В4 = b4 - ∆b4 = 175,3 – 12,3 = 163 мм.
Площадь поперечного сечения раската после четвёртой клети
F4 = h4×b4= 45,5 × 175,3 ≈ 8000 мм2.
Коэффициент вытяжки поперечного сечения раската в пятой клети:
µ 5 = F4 / F5 = 8000 / 7440 = 1,075 ≈1,08.
Клеть III. h3 =73 мм; b3 = 163,0 мм; D6 = 630 мм; η3 = 1,65.
Высота входящей полосы
H3 = h3 × η3 = 73×1,65 = 120 мм.
Обжатие
∆h3 = H3 – h3 = 120 – 73 = 47 мм.
Уширение

Ширина входящей полосы
В3 = b3 - ∆b6 = 163,0 – 16,6 = 146,4 мм.
Площадь поперечного сечения раската после третьей клети
F3 = h3 ×b3= 73 × 163 ≈ 11900 мм2.
Коэффициент вытяжки поперечного сечения раската в четвёртой клети:
µ 4 = F3 / F4 = 11900 / 8000 ≈1,48.
Так как получили большое обжатие, выполним проверку по условию захвата валками. При t = 1100ºС (валки стальные) максимальное обжатие составляет
∆hмакс3 = 0,77f23 R3 = 0,77×(1,05 – 0,0005×1100)2 ×315 ≈ 60 мм.
принятый коэффициент деформации удовлетворяет величине обжатия.
∆h3 < ∆h3 макс или 47 < 60 мм.
Клеть II. h2 =120 мм; b2 = 146,4 мм; D6 = 630 мм; η2 = 1,65.
Высота входящей полосы
H2 = h2 × η2 = 120×1,65 = 198 мм.
Обжатие
∆h2 = H2 – h2 = 198 – 120 = 78 мм.
Полученное значение ∆h2 значительно завышено и не может быть реализовано. Произведём проверку обжатия с учётом максимальной переточки валков по предельным условиям захвата
f2 = 1,05 – 0,0005t= 1,05-0,0005×1160 = 0,47.
При зазоре между валками 10мм, катающий диаметр составит:
Dк2 = D+S–h2 =630+10–120 = 520 мм.
∆h2 = hмакс2 = 0,77f22 R2 = 0,77 ×0,472 ×260 = 44 мм.
Высота раската перед второй клетью
Н2 = 120 + 44 = 164 мм
Уширение в клети II

Ширина входящей полосы
В2 = b2 - ∆b2 = 146,4 – 10 = 136,4 мм.
Площадь поперечного сечения раската после второй клети
F2 = Н2 ×В2 = 120 × 146,4 ≈ 17570 мм2.
Коэффициент вытяжки поперечного сечения раската в третьей клети:
µ 3 = F2 / F3 =17570 / 11900 ≈ 1,48.
Клеть I. Перед задачей раската во вторую клеть производят кантовку раската. При этом: h1 = В2 = 136,4 мм; b1 = Н2 = 164,0 мм; D6 = 630 мм; t = 1180ºС;
f 1 = 0,46; η3 = 1,65.
При зазоре между валками 15мм, катающий диаметр составит:
Dк1 = D+15 – h1 =630 + 10 – 120 = 508,6 мм.
Принимаем Dк1= 510 мм. Тогда обжатие составит:
∆h1 = hмакс1 = 0,77 ×0,462 ×255 ≈ 42 мм.
Высота заготовки
Н0 = 136,4 + 42 = 178,4 мм
Уширение

Ширина заготовки
В0 = b1 - ∆b1 = 164 – 8,5 = 155,5 мм.
Площадь поперечного сечения раската после первой клети
F1 = Н2 ×В2= 136,4 × 164 ≈ 22370 мм2.
Коэффициент вытяжки поперечного сечения раската во второй клети:
µ 2 = F1 / F2 = 22370 / 17570 ≈ 1,27.
Площадь поперечного сечения заготовки перед задачей в первую клеть:
F0 = Н0 ×В0= 178,4 × 155,5 ≈ 27650 мм2.
Коэффициент вытяжки поперечного сечения раската в первой клети:
|
|
|
µ 1 = F0 / F1 = 27650 / 22370 = 1,236 ≈1,24.
Результаты расчёта сводим в таблицу 11.4 и составляем схему прокатки полосы 18×160 мм, которая приведена на рисунке 11.11.
Таблица 15.4 – Таблица калибровки полосовой стали 18*160
| № прохода/ калибр | Толщина, H, мм | Обжатие, Dh, мм | К-т. дефом / относ.деф., η / Ԑ,% | Ширина, B, мм | Уширение, Db, мм | Площадь сечения, F, мм2 | К-т вытяжки, µ |
| 178,4 | |||||||
| 1 - пластовый | 1,23/18,42 | 150,0 | 1,24 | ||||
| 2 - / / - | 120,0 | 1,29 / 22,81 | 156,0 | 6,0 | 1,27 | ||
| 3 - / / - | 73,0 | 1,64 / 39,17 | 163,0 | 7,0 | 1,48 | ||
| 4 - / / - | 45,5 | 27,5 | 1,61 / 37,77 | 175,3 | 12,0 | 1,48 | |
| 175,3 | 45,5 | ||||||
| 5 - ребровой | 154,8 | 20,5 | 1,13 / 11,69 | 48,0 | 2,5 | 1,08 | |
| 48,0 | 154,8 | ||||||
| 6 - пластовый | 32,0 | 16,0 | 1,5 / 33,33 | 162,5 | 7,7 | 1,43 | |
| 7 - / / - | 22,8 | 9,2 | 1,36 / 28,75 | 167,5 | 5,0 | 1,36 | |
| 167,5 | 22,8 | ||||||
| 8 - ребровой | 159,5 | 8,0 | 1,05 / 4,78 | 22,8 | - | 1,05 | |
| 22,8 | 159,5 | ||||||
| 9 - пластовый | 18,25 | 4,55 | 1,23 / 19,96 | 162,0 | 2,5 | 1,23 |

Рис.11.10 – Схема прокатки полосы 18×160 на стане 500.
Константа калибровки - равенство секундных объёмов проходящих через каждую клеть в единицу времени.
C = F1×DK1 × n1 = • - • = Fi×DKi × ni = const [мм3об/мин].
где DK — катающий диаметр; ni — оборотs валков в конкретной клети
Окружная скорость валков определённая через DK × n:
V = π × DK × n / 60,
откуда: n9 = V9 × 60 / π × DK 9 = 9 ×60 / 3,14 × 0,54 = 318,5 ≈319 об/мин.
Тогда константа калибровки составляет:
К = F9×DK9 × n9 = 2960 ×540 × 319 = 509,89 ×106 ≈ 510×106 [мм3об/мин].
Скорость прокатки в клети №8 определяют после нахождения числа оборотов:
n8 = К /F8×DK9 = 510×106 / 3640×390 = 359 ≈ 360 об/мин.
Домашнее задание №2
Выполнить расчёт режима прокатки полосы из стали Ст.3сп в непрерывной группе клетей, в которой предчистовая клеть с вертикальным расположением валков. По результатам расчёта составить таблицу калибровки и схему прокатки
| № | Диаметр валков, D0, мм | Сечение полосы, H × B, мм | Материал полосы | Скорость прокатки, V, м/с |
| 36×8 | Сталь | |||
| 34×9 | Чугун | |||
| 48х×10 | Сталь | |||
| 55×12 | Чугун | |||
| 60×14 | Сталь | |||
| 65×8 | Чугун | |||
| 70×10 | Сталь | |||
| 75×12 | Чугун | |||
| 34×9 | Чугун | |||
| 55×10 | Сталь | |||
| 60×12 | Чугун | |||
| 63×14 | Сталь | |||
| 65×8 | Чугун | |||
| 70×10 | Сталь | |||
| 75×12 | Чугун | |||
| 80×14 | Сталь | |||
| 85×8 | Чугун | |||
| 90×10 | Сталь | |||
| 95×12 | Чугун | |||
| 100×14 | Сталь | |||
| 105×8 | Чугун | |||
| 110×10 | Сталь | 8,5 | ||
| 120×12 | Чугун | |||
| 125×10 | Сталь | 7,5 | ||
| 140×16 | Чугун | |||
| 135×18 | Сталь | |||
| 145×16 | Чугун | |||
| 150×18 | Сталь | |||
| 160×20 | Чугун | |||
| 180×10 | Сталь |
|
|
|


