для специальности 210402 «Средства связи с ПО»

Экзаменационные задачи по дисциплине ОТСПО

1. Вычислить вероятность Р_л.т. превышения порога х _п=3В случайной величиной x(t_i) с нормальным распределением и параметрами: а=0 и σ =2В, используя табулированный интеграл вероятности (П.2).

 

2. Гауссовская СВ x(t_i) с нулевым средним и σ =2В превышает порог х _п с вероятностью Р_л.т.=10^-2. Найти значение порога, используя табулированный интеграл вероятности (П.2).

 

3.Найти значение динамического диапазона Д (дБ) уровней сигнала с распределением по закону Релея (П.1), если за максимальный и минимальный допустимые уровни сигнала принять значения квантилей распределения порядка (1− α) и α = 0.0001 соответственно.

 

4. Найти среднее значение и дисперсию СВ с равномерным законом распределения (П.1), где a= − h/2, b=h/2.

 

5.Определить ХФ квадрата случайной величины Х с распределением Релея (П.1) и найти три первых начальных момента.

 

6.Определить энергетический выигрыш сигналов ОФТ по отношению к ЧТ (в дБ), если Р_ОФТ = 0.5 eхр( − h²), Р_ЧТ=0.5 eхр( − h²/2) и Р_ош=0,01.

 

7. Определить энергетический выигрыш сигналов ЧТ по отношению АТ

(в дБ), если Р_ош=0,001 и Р_ЧТ= 0.5 eхр( − h²/2), Р_АТ= 0.5 exp( − h²/4).

 

8. Определить энергетический выигрыш сигналов ФТ по отношению к ОФТ(в дБ), если Р_ош=0,001 и Р_ОФТ = 0.5 eхр( − h²) и Р_ФТ = 1−F(h√2).

 

9. Найти вероятность приема сообщения из 10 знаков пятиэлементного безызбыточного кода, если элементы независимы и вероятность ошибки приема элемента Р_ош=0,01.

 

10. Определить вероятность ошибки приема элемента сигнала ЧТ

Р_ЧТ= 0.5 eхр( − h²/2) со скоростью 500 бод в канале с АБГШ, если при скорости 50 бод вероятность ошибки Р_ош=0,01.Что необходимо сделать, чтобы значение Р_ош=0,01 оставалось неизменным.

 

11.На вход последовательно соединенных сопротивления R и емкости С (ФНЧ) воздействует белый шум со спектральной плотностью Ѕ(ω)=Ν_о/2. Найти спектральную плотность Ѕ(ω) напряжения на С и функцию корреляции

 

12. На вход линейного фильтра поступает смесь х(t)=s(t)+n(t), где n(t) – стационарный АБГШ, а s(t) – статистически независимый от шума экспоненциальный видеоимпульс

Найти передаточную функцию K(jω) фильтра, максимизирующего отношение сигнал/ шум на выходе.

 

13.Найти передаточную функцию фильтра, максимизирующего выходное отношение сигнал шум, если на вход воздействует aддитивная смесь x(t)=S(t)+n(t), где

 

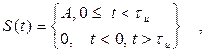
а n(t) - стационарный шум со спектральной плотностью

 

.14. Задан модулирующий НЧ сигнал без возвращения к нулю (БВН), который является центрированным стационарным процессом, принимающим с равной вероятностью значения +1 и −1. АКФ сигнала БВН равна:

Найти СПМ сигнала БВН (синхронного телеграфного сигнала).

 

15. Сигнал с корабля в режиме сверх быстродействия (СБД) принимается базовой радиостанцией на N разнесенных в пространстве антенн. Считается, что замирания медленные и происходят на разных антеннах независимо по закону Релея. Телеграмма не может быть принята, если уровень сигнала ниже, чем σ/k, где k=3. Определить вероятность приема телеграммы на одну, на две и на три антенны.

 

16. Вычислить спектр сигналов и построить графики:

1. u₁(t) = cos ω₀t + j sin ω₀t

2. u₂(t) = cos ω₀t − j sin ω₀t

17. Вычислить среднюю вероятность ошибки некогерентного приема сигнала при АБГШ и М-кратном разнесенном приеме с автовыбором ветви разнесения по экстремальному алгоритму, где М=2, - среднее по замираниям ОСШ в ветви на входе РПУ, а замирания в ветвях независимы.

 

18. Вычислить среднюю вероятность ошибки некогерентного приема сигнала при АБГШ и М-кратном разнесенном приеме с со сложением независимых ветвей по Бреннану, где М=2, - среднее по замираниям ОСШ на входе РПУ ветви гауссовского канала связи.

 

19. Вычислить верхнюю границу средней вероятности ошибки приема кодового слова БЧХ (7, 4) при d_min =3 и вероятности ошибки символа слова 10⁻¹ .

 

. 20. Вычислить d_min и верхнюю границу средней вероятности ошибки приема кодового слова т- последовательности при т =3 и вероятности ошибки символа 10⁻¹ .

 

. 21. Линейный блоковый (n,k) код (7,4) задан порождающей матрицей:

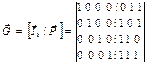
Найти выражения для проверочных бит передаваемого слова, проверочную матрицу 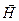, решить уравнение ортогональности для принимаемых кодовых слов С _т ∙Н^Т = 0 и результат сравнить с выражениями для проверочных бит кодового слова.

 

22. Дана порождающая матрица линейного двоичного кода (7,3)

Привести к систематической форме, найти проверочную матрицу 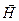, матрицу синдромного декодирования Н^Т. Найти верхнюю границу d_min и кратность исправления ошибок.

 

23. Дана порождающая матрица линейного двоичного кода (7,3)

Показать, что кодовое слово С_m для информационной последовательности Х _m [101] ортогонально к матрице . Построить проверочную матрицу расширенного кода (8,3), укороченного кода (6,2); найти верхнюю границу d_min и кратность исправления ошибок.

24. Циклический код (7,4) задан порождающим полиномом q(p)=p³+p+1. Построить на регистрах сдвига кодер ЦК.

Найти порождающую матрицу в систематическом виде и проверочную матрицу 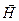. Вычислить верхнюю границу d_min и кратность исправления ошибок.

 

25. Найти порождающую матрицу _д в систематическом виде для ЦК (7,3), дуального коду (7,4), по проверочному полиному h(p)=(p+1)(p³+p²+1). Вычислить верхнюю границу d_min и кратность исправления ошибок.

26. Построить схему сверточного кодера с кодовым ограничением К=4 и скоростью ½ по порождающим полиномам g₁ = 15 и g₂ = 17 в восмеричной форме записи.

Поделиться:

Воспользуйтесь поиском по сайту: