 |
Голографическое изображение точки
|
|
|
|
Физические принципы голографии.
Период световых колебаний чрезвычайно мал, так что любой приемник излучения регистрирует лишь интенсивность (усредненный квадрат амплитуды), но не фазу. Но именно фаза содержит в себе информацию о взаимном расположении частей источников света.
Например, источники S1 и S2 оба дают равномерное
освешение экрана. И даже если, например, получим
изображение с помощью линзы, информация не будет полной (на фотографии невозможно отличить, снят ли малый предмет с близкого расстояния, или – большой с далекого. Разобраться в этом помогает только критическое отношение ко всему снимку в целом).
Таким образом: для полного представления о локализации световой волны нужно уметь измерять распределение амплитуд и фаз волны. Это можно сделать, используя явление интерференции. Действительно, сущность интерференции как раз и заключается в том, что при сложении когерентных колебаний суммарная амплитуда определяется разностью фаз этих колебаний. Следовательно, если на приемник излучения послать интересующую нас волну и одновременно другую, опорную, с простой (и известной) формой фронта, например, плоскую, то возникшая интерференционная картина полностью охарактеризует закон изменения разности фаз этих двух волн на поверхности приемника (обычно – фотопластинки). Разумеется, эти волны должны быть когерентными. Рассмотрим самые простые случаи - голографическое изображение плоской волны и голографическое изображение точки.
Голографическое изображение плоской волны
Получение голограммы. 
Организовать опорную и исследуемую волну можно, например, поставив на пути плоской волны бипризму Френеля. Фронт волны делится на два и получаются две плоские волны, которые сходятся под углом 2u. Справа – опорная волна, слева – исследуемая (можно и наоборот) Интерференционная картина получается в виде полос с синусоидальным распределением интенсивности. Ширина полосы равна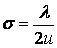 
. (Это мы получили раньше, когда рассматривали интерференцию света от двух когерентных источников) Фотографируем получившуюся интерференционную картинку. Это и есть голограмма плоской волны..
|
|
|
Восстановление голограммы.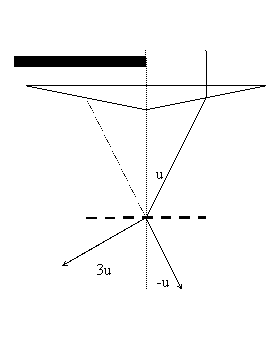 
Освещаем голограмму опорной волной такой, как при получении голограммы. Теперь голограмма работает как дифракционная решетка, на которую падает волна под углом u. Для косого паления лучей на решетку мы получили формулу
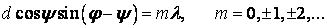
Но в нашем случае углы малы, так что косинус можно считать равным единице, а синус – углу. Угол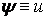 
– это угол падения. Постоянная решетки 
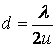. Кроме того, в силу того, что штрихи решетки не резкие, а их прозрачность меняется по синусоидальному закону, виден только первый порядок дифракции, 
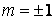, более высокие порядки не видны вовсе, а нулевой порядок – ослаблен. (это можно показать простым расчетом). Поэтому в нашем случае получим 
и значит угол дифракции, соответствующий максимуму равен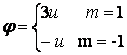 
Угол 
отсчитывается от нормали к плоскости решетки (голограммы).
Угол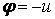 
соответствует исследуемой волне – «восстановленная волна». Кроме того, присутствует и еще одно изображение.
Голографическое изображение точки
Получение голограммы. Маленький («точечный») объект S освещается опорной волной и та же волна посылается на экран. Она интерферирует с волной, отраженной от S. Эти две волны когерентны, но одна – плоская, другая – сферическая. На экране получается интерференционная картинка в виде колец, аналогичным кольцам
|
Ньютона. Максимумы интенсивности (светлые кольца) будут там, где разность хода Δ лучей от опорной волны и волны от точечного источника S будет равна целому числу длин волн. Сфотографировав картинку получим голограмму точки.
|
|
|
Замечание. Радиусы колец голограммы отличаются от радиусов колец Ньютона, полученных для тех же фронтов волн – они больше на величину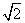 
. Это потому, что разность хода двух лучей при наблюдении колец Ньютон будет 2Δ, так как луч проходит это расстояние дважды.
Восстановление голографического изображения.
Голограмма точки является фазовой пластинкой с фокусом, равным расстоянию SO. Действительно, радиусы колец определяются условием, что длина лучей, проведенных из точки S до соседних колец отличаются на длину волны. Следовательно, каждое кольцо (которое является суммой темного и светлого участков) включает в себя две зоны Френеля. Одна из этих зон закрыта (темный участок), другая открыта (светлый участок), а это и есть зонная пластинка.
Теперь понятно, как можно восстановить голографическое изображение.
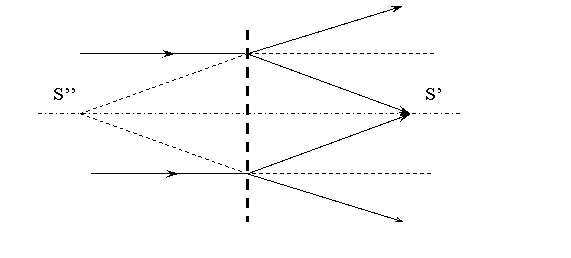Осветим голограмму плоской волной (с той же длиной волны). Голограмма, как и зонная пластинка, даст два изображения источника – действительное S’ и мнимое. S’’. Мнимое изображение совпадает с «исходным» – источником S. Других изображений (фокусы зонной пластинки высших порядков) не возникает, так как распределение интенсивности в зонной пластинке синусоидальное (это можно показать точным расчетом).
|
|
|
