 |
Принцип Гюйгенса – Френеля
|
|
|
|
Интерференция волн
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн по отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение носит название принципа суперпозиции волн.
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, происходят с одной частотой и обладают постоянной во времени разностью фаз, волны называют когерентными.
При наложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.
Выясним, почему это происходит и каким условиям должны удовлетворять точки среды, чтобы в них наблюдалось усиление или гашение колебаний.
Пусть в некоторой области пространства распространяются две плоские волны одинаковой частоты w. Выясним, как будет вести себя произвольная точка Р среды, до которой доходят обе волны.
 |
Согласно принципу суперпозиции точка Р должна прийти в два колебательных движения:
где j1 - запаздывание первой волны по фазе, j2 - запаздывание второй волны по фазе.
 |
Суммарное смещение точки Р будет равно
Складывать гармонические функции одной частоты удобно, используя метод векторных диаграмм.
Амплитуда результирующего колебания А находится по теореме косинусов:
 |
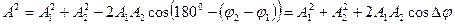где Dj - разность фаз волн, приходящих в точку Р.
 |
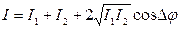Поскольку интенсивность волны пропорциональна квадрату амплитуды, можно записать
|
|
|
Получили потрясающий результат!! Две волны приходят в точку, но энергия, приносимая в эту точку не равна сумме энергии каждой волны! Почему? Не нарушается ли здесь закон сохранения энергии?
Все дело в соsDj. Он может быть положительным – это будет означать, что энергия, приходящая к данную точку среды больше суммарной энергии двух волн. Колебания в этой точке усилились. Но ведь будут и такие точки среды, для которых соsDj отрицателен. Энергия, приходящая в эти точки, меньше суммарной энергии двух волн. Энергия двух волн просто перераспределилась между точками среды. За счет этого некоторые точки стали колебаться с большей амплитудой, а некоторые – с меньшей.
Очевидно, будут такие точки среды, для которых соsDj = 1. Энергия, приносимая волнами в эти точки, самая большая, они будут колебаться с максимально возможной амплитудой. Говорят, что для таких точек выполняется условие максимума. Волны, приходящие в точку, должны быть синфазные, т.е. Dj = 0, 2p, 4p,…
Если амплитуды волн одинаковы, то точки, для которых выполняется условие максимума, колеблются с амплитудой А = А1 + А1= 2А1, а энергия этих точек увеличивается в 4 раза в сравнении с тем, если бы точки совершали колебание в одной волне.
 |
Найдутся такие точки среды, для которых соsDj = -1. Энергия, приходящая в эти точки, будет наименьшей, и колебаться эти точки будут с самой маленькой амплитудой.
Говорят, что для таких точек выполняется условие минимума. Нетрудно видеть, что волны, приходящие в этом случае в точку, должны быть в противофазе, т.е. Dj = p, 3p,…
Если волны, приходящие в точку, для которой выполняется условие минимума, имеют одинаковые амплитуды, то, легко видеть, что I = 0 и А = 0. Точки просто не колеблются!!! Волны не просто ослабили друг друга, они полностью погасили друг друга.
Подведем некоторые итоги.
1. В результате наложения когерентных волн наблюдается интерференционная картина – все точки среды колеблются, но амплитуды колебания точек разные. Эти амплитуды с течение времени не меняются, то есть картинка распределения амплитуд в пространстве остается неизменной. Говорят, что получилась устойчивая картина наложения. Устойчивая – не значит неподвижная! Все колеблются!
|
|
|
2. В некоторых точках среды волны усилили друг друга, точки колеблются с амплитудой, превышающей амплитуду каждой из волн в отдельности. Сюда поступает больше энергии.
3. Среди точек, в которых произошло усиление колебаний, можно выделить точки максимума – их амплитуда колебаний самая большая. Для того, чтобы в какой-либо точке выполнялось условие максимума, в нее должны приходить синфазные волны: Dj = 0, 2p, 4p,…
4. В некоторых точках среды волны будут ослаблять друг друга – амплитуда колебания точек будет меньше, чем в каждой из волн в отдельности. В эти точки поступает меньше энергии.
5. Среди точек, в которых произошло ослабление колебаний, выделяют точки минимума – амплитуда колебания этих точек самая маленькая, в эти точки приходит самое маленькое количество энергии. В точках минимума может наблюдаться полное гашение колебаний, если амплитуды накладывающихся волн равны. В точки минимума волны должны приходить в противофазе: Dj = p, 3p,…
Осталось выяснить, откуда берется разность фаз волн, приходящих в какую-либо точку среды.
Во-первых, сами источники могут колебаться в разных фазах.
Во-вторых, расстояния, проходимые волнами, от источников до наблюдаемой точки, в общем случае разные.
Разность расстояний от источников до рассматриваемой точки называется разностью хода волн
Разность хода дает разность фаз, которую несложно рассчитать через длину волны (пока мы рассматривает случай, когда волны распространяются в одной среде):
В общем случае разность фаз волн, приходящих в какую-либо точку среды, равна
.
Все становится намного проще, если источники волн колеблются в одной фазе. Тогда разность фаз волн обусловлена только их разностью хода. В этом случае условия максимума и минимума можно сформулировать иначе.
Для точек максимума на разности хода должно укладываться целое число длин волн:
|
|
|
 |
 |
Для точек минимума на разности хода должно укладываться нечетное число полуволн:
Стоячие волны
Частным случаем интерференции является наложение падающей и отраженной волны, бегущей в противоположном направлении. Такое явление наблюдается, если дернуть за струну музыкального инструмента. По ней побежит волна, она отразится от точки закрепления струны, и мы будем наблюдать результат наложения падающей и отраженной волн.
Очень важный случай интерференции наблюдается при наложении встречных волн одной амплитуды. Исследуем эффект теоретически.
Уравнение бегущей волны
Уравнение встречной волны
Результирующее колебание
 |
Нетрудно видеть, что в результате наложения двух встречных волн все точки колеблются с той же частотой w, что и встречные волны. Но вот амплитуды разных точек на оси ОХ, вдоль которой распространялись волны, разные.
В точках, координаты которых удовлетворяют условию
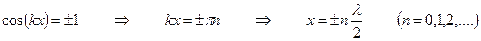
амплитуда колебаний достигает максимального значения 2А. Эти точки называются пучностями стоячей волны.
В точках, координаты которых удовлетворяют условию
Амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны. Точки, находящиеся в узлах стоячей волны, колебаний не совершают!!!
Расстояние между соседними узлами, как и между соседними пучностями, равно l/2. Пучности и узлы сдвинуты относительно друг друга на четверть длины волны.
На рисунке показан ряд моментальных «фотографий» отклонения точек от положения равновесия в стоячей волне. Стрелками показаны скорости частиц.
Все точки, расположенные между двумя соседними узлами, колеблются в одной фазе: они одновременно проходят положение равновесия и одновременно приходят в положение максимального отклонения от положения равновесия.
Видно, что точки по разные стороны от узлов колеблются в противофазе.
Почему стоячие волны столь важны в физике?
Вернемся к струне, закрепленной с двух сторон. При возбуждении колебаний в ней устанавливается стоячая волна. Причем в местах закрепления у этой волны должны располагаться узлы, ибо эти точки колебаться не могут. Поэтому в струне возбуждаются с заметной амплитудой только такие колебания, половина длины которых укладывается на длине струны целое число раз. Например, закрепленная струна может совершать следующие колебания:
|
|
|
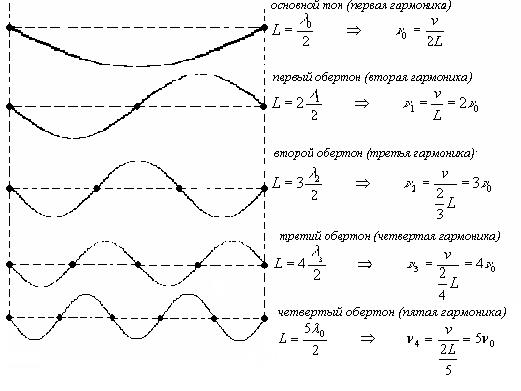и т.д.
Частоты n0, n1, n2, n3 и т.д. называются для струны собственными частотами (или нормальными колебаниями). В общем случае колебания струны представляет собой наложение различных гармоник, т.е. струна одновременно участвует в нескольких собственных колебаниях.
Наибольшая амплитуда колебаний, как правило, будет на частоте основного тона. Чем выше номер гармоники, тем амплитуда колебаний будет меньше. Поэтому основной тон мы и слышим громче всего.
Важно!!
Струна в отличие от маятника имеет целый набор собственных частот колебаний! Сравните – маятник может совершать собственные колебания только с одной, собственной, частотой.
Любое тело подобно струне имеет набор собственных частот колебаний. Эти частоты соответствуют частотам стоячих волн, которые могут устанавливаться в теле. Очевидно, что собственные частоты или частоты стоячих волн будут зависеть от геометрических размеров и формы тела (они определяют длину волны), а также от вещества, из которого изготовлено тело (оно определяет скорость распространения волны в теле).
Если на тело будет действовать внешняя периодически меняющаяся сила с частотой, совпадающей с одной из собственных частот тела, возникнет резонанс. Это свойство используется при создании приборов для измерения частоты колебаний (частотомеров), для усиления звука (резонаторные ящики музыкальных инструментов).
С инженерной точки зрения возможность резонанса, как правило, играет отрицательную роль. Любая строительная конструкция (мост, стена здания, плита перекрытия и т.д.), корпус двигателя (станка, самолета и т.д.) способны резонировать на определенных частотах. Важно, чтобы при расчете инженерных конструкций возможные частоты внешних воздействий были далеки от собственных. Задача усложняется еще и тем, что резонировать может не вся конструкция в целом, но и отдельные ее части.
Принцип Гюйгенса – Френеля
В 1690 году Гюйгенс сформулировал принцип, позволивший объяснить процесс распространения волн и из свойства – отражение, преломление и дифракцию.
Суть принципа заключается в следующем: каждая точка среды, до которой дошел волновой процесс, становится источником вторичных сферических волн. Чтобы построить волновой фронт, нужно провести огибающую этих вторичных сферических волн.
|
|
|
Физическое толкование принципа Гюйгенса было дано Френелем: вторичные сферические волны когерентны, они интерферируют. В направлении распространения волны вторичные сферические волны, интерферируя, усиливают друг друга, в противоположном направлении – гасят.
Применим принцип Гюйгенса – Френеля к объяснению явлений отражения и преломления.
Отражением называют явление возвращения волны в первоначальную среду при попадании на границу раздела двух сред.
Пусть на границу раздела двух сред падает плоская волна.
Углом падения называют угол между направлением распространения волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения (на рис. угол α).
Видно, что волна дошла до всех точек границы, расположенных левее точки А. Эти точки колеблются, от них бегут вторичные сферические волны.
За то время t, что падающая волна дойдет от точки В до точки С, расположенной на границе раздела, все точки отрезка АС будут вовлечены в колебательный процесс, от них побегут вторичные сферические волны. Волновой фронт отраженной волны строится как огибающая этих вторичных сферических волн.
Направление распространения отраженной волны перпендикулярно фронту отраженной волны. Угол между направлением распространения отраженной волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения, называется углом отражения (на рис. угол β).
Рассмотрим прямоугольные треугольники ABC и ADC.
Сторона АС в этих треугольниках общая. Расстояние АD – это путь, пройденный вторичной волной за то время, пока падающая волна идет от В до С:
где v – скорость распространения волны.
Таким образом, ∆ABC = ∆ADC. В равных треугольниках против равных сторон (
) находятся одинаковые углы α = β. Угол падения равен углу отражения.
Преломлением называется изменение направления распространения волны при переходе из одной среды в другую.
Пусть плоская волна переходит из среды, где скорость ее распространения равна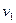 
, в среду, где скорость распространения волны 
.
За то время t, что падающая волна дойдет от точки В до точки С, расположенной на границе раздела, все точки отрезка АС будут вовлечены в колебательный процесс, от них побегут вторичные сферические волны во вторую среду. Волновой фронт отраженной волны строится как огибающая этих вторичных сферических волн.
Направление распространения прошедшей во вторую среду волны перпендикулярно фронту отраженной волны. Угол между направлением распространения прошедшей волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения, называется углом преломления (на рис. угол α2).
В прямоугольных треугольниках ABC и ADC
Находим отношение синусов углов падения и преломления
Полученный результат свидетельствует о том, что причиной изменения направления распространения волны при переходе из одной среды в другую является изменение скорости волны.
Дифракция – явление огибания волнами преград и попадания в область геометрической тени.
Например, вы слышите музыку, находясь по обратную сторону летней эстрады. Стоя за глухим высоким забором школьного стадиона, вы слышите крики болельщиков. Круговая волна на поверхности воды, проходя через зазор в преграде, распространяется не параллельным пучком, а расходится, попадает в области за преградой.
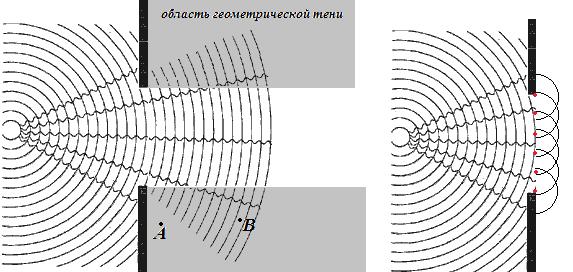
Качественное объяснение явлению можно дать, опять-таки используя принцип Гюйгенса – Френеля. От каждой точки отверстия распространяется вторичная сферическая волна. Оказывается, что в области геометрической тени вторичные сферические волны, интерферирую, не гасят друг друга. Таким образом, волна огибает преграду, попадает за преграду. Степень расхождения волны после прохождения отверстия (преграды) зависит от размеров отверстия, длины волны и удаленности наблюдателя от отверстия (в точке А на рисунке волны нет, а в точку В волна пришла). Чем меньше отверстие (преграда), тем степень расхождения (схождения) волны за ней будет больше.
Примеры решения задач
|
|
|
