 |
Эквивалентная схема участка длинной линии
|
|
|
|
ЦЕЛЬ РАБОТЫ
Экспериментально изучить режимы работы длинной линии.
КРАТКИЕ ПОЯСНЕНИЯ
Линии связи (ЛС) в EWB представлены двумя моделями: идеальной двухпроводной ЛС без потерь,и с потерями. Математическая модель ЛС с потеря-ми состоит из набора одинаковых звеньев. Первичные пара-метры линии имеют обозначение:
R — активное (омическое) сопротивление проводников ЛС, отнесенное к единице длины (погонное сопротивление), Ом/м; для реальных ЛС в зависимости от ее конструкции к этому сопротивлению добавляются активные сопротивле-ния потерь, вызванные поверхностным эффектом (плот-ность тока у поверхности проводника больше, чем в цент-ре), эффектом близости (эффект взаимодействия вихревых токов проводников ЛС, возникающих под действием маг-нитного поля проводников из-за протекающих по ним то-ков) и вихревыми токами, наводимыми в окружающих ЛС проводящих поверхностях (например, в металлическом экране);
L — погонная индуктивность проводников ЛС, Гн/м;
G — погонная проводимость между проводниками ЛС, См/м; для реальных ЛС к этой проводимости добавляются проводимости, вызванные диэлектрическими потерями изоляционных материалов;
С — погонная емкость между проводниками, Ф/м.
3.2 Диалоговое окно с потерями ЛС
Значения параметров ЛС в EWB 4.1 задаются с помощью диалоговых окон на рис. 3.2 и 3.3. В окне на (рис. 3.2) зада-ются значения параметров эквивалентной схемы на (рис. 3.1, в) (с индексом <<t>> для EWB 4.1), длину ЛС LEN, м (LEN в EWB 5.0) и параметр n, определяющий количество элементарных секций в ЛС выбранной длины LEN (в EWB 5.0 этот параметр отсутствует). Параметр n может быть выбран в пределах от 1 до 128 в одном компоненте на рис. 3.1, б; сели этого недостаточно, то последовательно включается несколько таких компонентов.
|
|
|
В диалоговом окне для идеальной (R. = О, G = О) ЛС
обозначено: 
— волновое сопротивление, Ом;
Td — время задержки распространения сигнала, с (параметры 
и TD в EWB 5.0).
Выражение для волнового сопротивления наглядно полу-чается из условия равенства энергии электрического поля конденсатора и магнитного поля индуктивности для идеальной ЛС. Это условие для амплитуд тока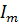 
и напряжения 
запишется в виде известной формулы
(
откуда волновое сопротивление
Время задержки сигнала при прохождении ЛС длиной L определяется формулой:
TD-1/с
где с — скорость распространения электромагнитного поля вдоль линии, принимается равной скорости света в вакууме (3 
м/с)
При наличии диэлектрика скорость распространения может уменьшиться на 10...15% и более (определяется коэффициентом укорочения волны, приблизительно равном корню квадратному из диэлектрической проницаемости диэлектрика). Скорость распространения связана с параметрами ЛС следующим соотношением:
C=1/ 
Если принять, что длина ЛС LEN измеряется в метрах и скорость распространения равна 3-10' м/с, то на основании выражения (3.3) параметры L и С необходимо выбирать из условия
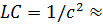11.11* 
Только при соблюдении условия (3.4) будет однозначная связь между длиной линии в метрах, погонной емкостью в Ф/м, погонной индуктивностью в Гн/м и, как следствие— возможность сопоставления результатов моделирования с результатами приведенных ниже расчетов. С учетом после-днего обстоятельства целесообразно также обеспечить ус-ловие независимости волнового сопротивления, определяе-мого формулой (3.1), от частоты (условие неискажающей ЛС), которое имеет следующий вид:
Режим бегущей волны характерен для ЛС, на выходе которой включено активное сопротивление, равное волновому сопротивлению 
. Для такого режима мгновенное значение напряжения в любой точке ЛС описывается следующим выражением:
|
|
|
) (3.6)
где l — расстояние от начала ЛС до точки, в которой определя-ется значение напряжения;
— частота входного сигнала Ui;
— постоянные затухания и сдвига фазы
; (3.7)
= 
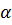; 3.8
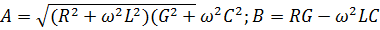
Из формулы (3.6) видно, что амплитуда бегущей волны на-пряжения убывает вдоль линии по экспоненциальному закону.
Если выполняются условия R 
L и G 
C,то для определения постоянной затухания и сдвига фазы пользуются приближенными выражениями:
+G 
; 
Для моделирования ЛС в режиме бегущей волны исполь-зуем схему на рис. 3.4. Значения параметров ЛС LТ1: LEN = 100 м, R = 1 Ом/м, n = 100. Задаемся значением L = 11,11 мкГн/м, после чего с помощью формул (3.4), (3.1) и (3.5) находим С = 1 пФ/м, = 3333 Ом, G =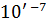 
См/м.
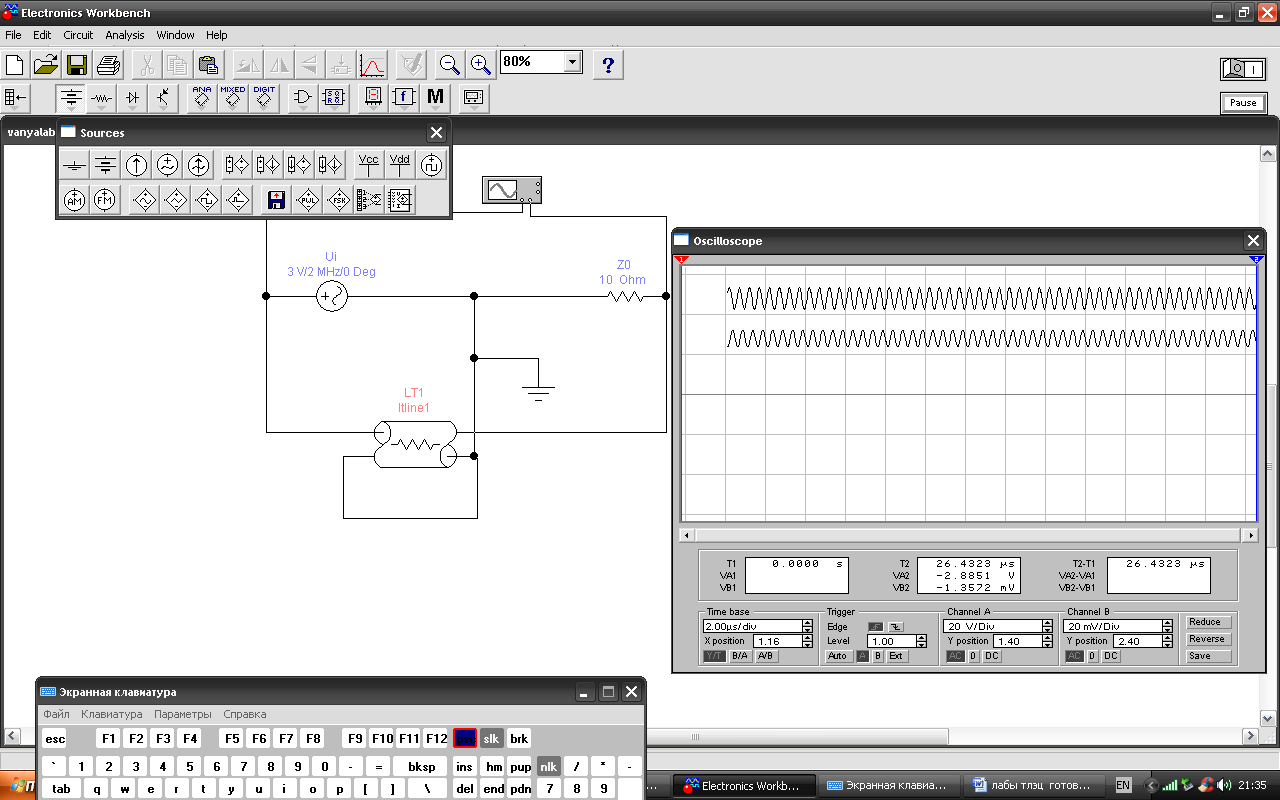
Результаты моделирования ЛС представлены в виде осциллограмм напряжения. Из них видно, что выходное напряжение опаздывает (см. правое индикаторное окно) на Т2 — T] = 0,33 мкс, что при частоте входного сигнала 500 кГц (период 2 мкс) соответствует а = 1,0362 рад на 100 м. По формулам (3.9) получаем а = 0,1046 рад/м и 
= 0,000154 — 0,00017 = 0,00032 неп/м (непер — единица затухания, применяемая чаще всего в проводной связи и равная 8,68 дБ), т.е. расчетное значение фазовой постоян-ной на 100 м составляет 1,046 рад, что близко к полученно-му при моделировании. Из индикаторных окон видно, что амплитуда входного напряжения 
= VA1 = 4,243 В, а выходного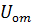 
= VB2 = 4,14 В. Согласно (3.6), расчетное значение U, = 
ехр(-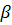 
1) = 4,11 В, что тоже близко к полученному при моделировании.
Рис. 3.4. Схема включения ЛС для испытания ее в режиме бегущей
волны
Режим не согласованной линии характеризуется тем, что на ее выходе включено сопротивление Z, не равное волновому сопротивлению ZO. Наиболее ярко этот режим прояв-ляется при разомкнутой (Z = 
) или замкнутой (Z = О) ли-нии. При разомкнутой линии бегущая волна тока достигает конца линии, и заряды дальше двигаться не могут. Ток дол-жен прекратиться. Но убывание тока создает по правилу Ленца ЭДС самоиндукции, направленную попутно с убывающим током, Появление же этой ЭДС приводит к повышению напряжения на конце линии, что в свою очередь вызывает движение зарядов в обратном направлении.
Следовательно, дойдя до разомкнутого конца линии, волны вынуждены двигаться в обратном направлении. Это явление называется отражением волны от конца линии. Энергия отраженных волн возвращается к началу линии, Электрические заряды прямой и обратной волн у конца провода складываются, в результате чего в этом месте в каждый момент времени получается удвоенное напряжение.
|
|
|
Для характеристики линии в рассматриваемом режиме используется коэффициент отражения:
P= (Z- ) / (Z+ )
При Z = коэффициент р = 0 и в линии наступает режим бегущей волны. При разомкнутой линии Z = и р = 1. При этом в конце линии амплитуды напряжения и тока определяются выражениями:
= 
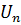(1+p) = 0; = 
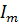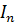(1-p) = 2 .
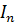Следовательно, при разомкнутой линии ток в ее конце равен нулю, а амплитуда напряжения равна двойной амплитуде падающей волны 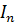. При этом падающие и отраженные волны напряжения имеют одинаковую фазу, а волны тока — противоположную.
Наиболее просто моделируется режим разомкнутой ли-нии. Для этого достаточно удалить сопротивление в схе-ме на рис. 3.4, уменьшить до минимума потери (установле-но R = 0,001 Ом/м, G = 
См/м) и изменить частоту вход-ного сигнала таким образом, чтобы на длине линии LEN укладывалось целое число длин волн. Выберем длину вол-ны 50 м, что соответствует частоте входного сигнала 3 
/50 = 6 Мгц. При этом результаты моделирования для этого случаям будут показаны в новом диалоговом окне, отку-да видно, что при входном напряжении Ui = 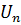= Val= 4,24 В напряжение в конце линии U = VB2 = 8,44 В, что близко к ожидаемому. Видно также, что отраженная волна опазды-вает от падающей на Т2 — Tl = 1,8 нс, что составляет около 0,067 рад (
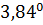), что объясняется несовершенством модели и погрешностью моделирования.
1. Длинные линии широко применяются в качестве соединительных линий, например линий, соединяющих антенну с приемником или передатчиком. В усилителях СВЧ вместо колебательных контуров используютрезонирующие отрезки длинных линий, в качестве согласующих элементов - отрезки длинных линий, трансформирующие сопротивления, для измерительных целей - измерительные линии, для формирования кратковременных импульсов, осуществления фазового сдвига, задержки импульсов и высокочастотных колебаний - линии задержки
|
|
|
Эквивалентная схема участка длинной линии
Эквивалентная схема участка длинной линии. Стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz
Значения параметров схемы определяются соотношениями:
| (1) |
Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:
Подставляя сюда значения параметров схемы из (1), получаем:
Из последних соотношений находим дифференциальные уравнения линии. Эти уравнения определяют связь между током и напряжением в любом сечении линии и называются телеграфными уравнениями длинной линии.
3 При R= 10 Ом
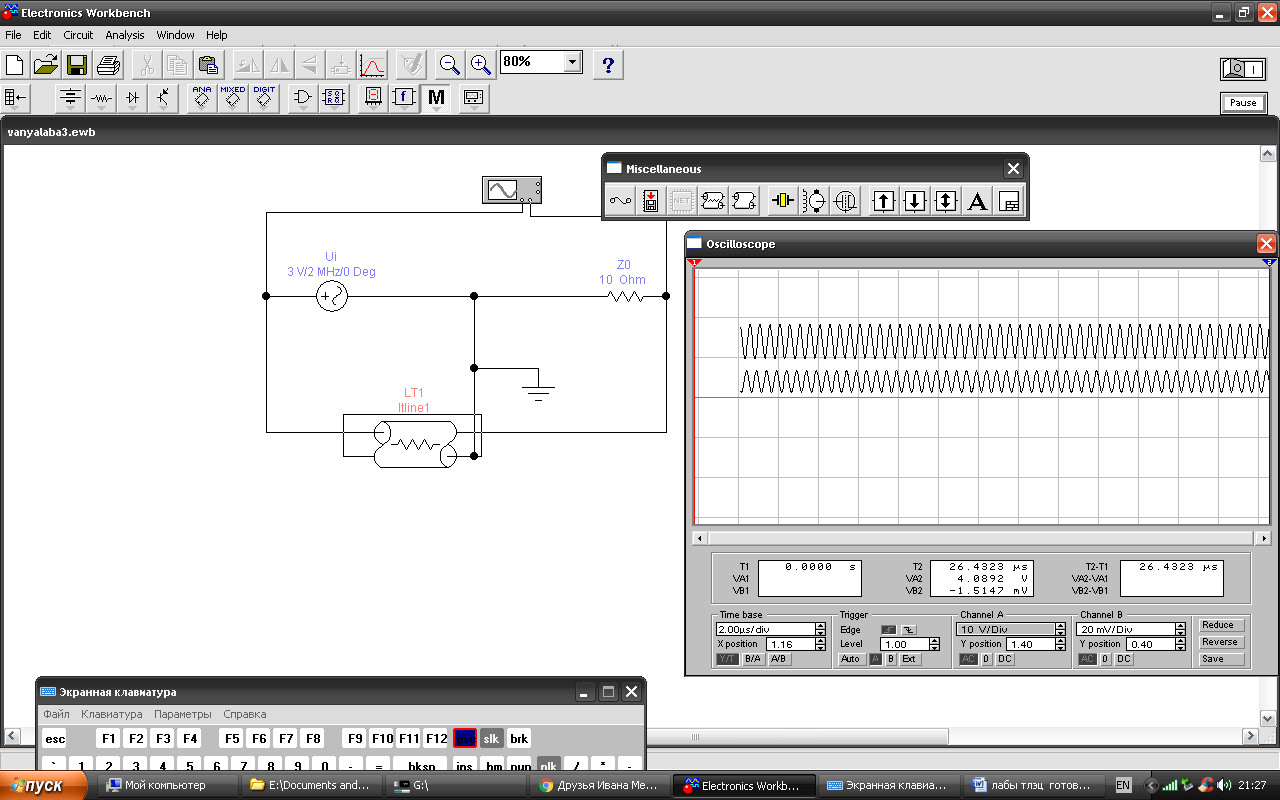
4 При частоте равной 3 МГц при разомкнутых линиях связи
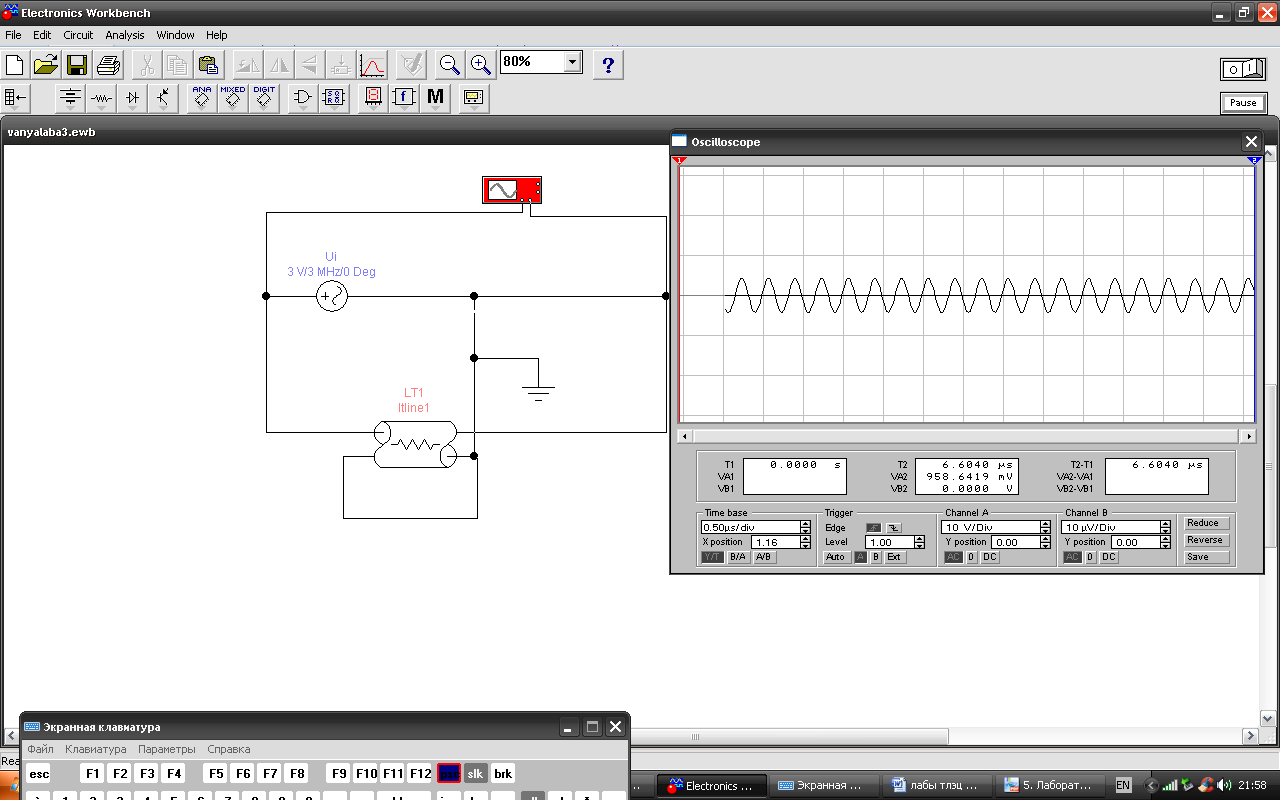
5 При частоте равной 2 МГц
|
|
|
