Примеры решения задач по парной регрессии.

 

Задача 1. Исследуя спрос на продукцию фирмы, аналитический отдел собрал данные по 20 торговым точкам компании и представил их в виде:

ln y = 6,8 – 0,6 ln x + ε,

(2,7) (-2,8)

где y – объем спроса,

x – цена единицы продукции.

В скобках приведены фактически значения t – критерия.

Ранее предполагалось, что увеличение цены на 1% приводит к уменьшению спроса на 1,2%. Можно ли утверждать, что приведенные результаты подтверждают это предположение?

Решение:

Уравнение регрессии в прологарифмированном виде. Судя по форме записи, уравнение имеет степенной вид и записывается так:

Надо проверить предположение о том, что эластичность спроса по цене равна –1,2. В степенной зависимости эластичность равна показателю степени b, поэтому оценка эластичности равна –0,6. Таким образом, задача сводится к проверке статистической гипотезы (нуль - гипотезы) H₀:b=-1,2 против альтернативной H₁:b≠-1,2. Критическая область двусторонняя, поэтому проверка гипотезы может быть заменена построением доверительного интервала для b и, если проверяемое значение b=-1,2 попадает в него, то нуль-гипотеза не отклоняется; в противном случае принимается альтернативная гипотеза.

Интервал строится по формуле (23):

-0,6- m_b · t_таб < b < -0,6+ m_b · t_табл.

Определим стандартную ошибку параметра b из формулы (21):

m_b = = = 0,2143

Для определения t_табл зададим уровень значимости, равный 0,05, следовательно:

t_табл (α; n-2) = t_табл (0,05;18) = 2,1

(используем таблицу критических точек распределения Стьюдента для двустороннего α=0,05).

Доверительный интервал равен:

-0,6-0,2143·2,1 < b < -0,6+0,2143·2,1

или

-1,05 < b < -0,15.

Значение, равное –1,2, в интервал не попадает, следовательно, предположение о значении коэффициента эластичности на уровне значимости 0,05 следует отклонить. Однако, если задать значимость на уровне 0,01, то t_табл=2,88, и интервал будет таким:

-1,217 < b < 0,017

Следовательно, на уровне значимости 0,01 первоначальное предположение не может быть отклонено, поскольку значение –1,2 попадает в доверительный интервал.

Можно проверить статистическую гипотезу напрямую, вычислив t –статистику для разницы между гипотетическим и вычисленным значениями b:

= = = 2,8.

Сравним полученную статистику по абсолютной величине с критическим значением на заданном уровне значимости. На уровне α=0,05:

;

Нуль-гипотеза отклоняется, эластичность спроса по цене не может быть равна –1,2. На уровне α=0,01:

;

нуль-гипотеза не отклоняется, эластичность может быть равна –1,2.

■

 

Задача 2. Для двух видов продукции А и Б зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

= 15 + 8·lnx,

= 25x^0,3.

Сравнить эластичность затрат по каждому виду продукции при x =50 и определить объемы продукции обоих видов, при котором эластичности будут одинаковы.

Решение Регрессионная зависимость для продукции А является полулогарифмической, и для вычисления эластичности воспользуемся формулой:

Э_А = = = 0,173.

Для продукции Б регрессионная зависимость является степенной, где коэффициент эластичности равен показателю степени при любых значениях независимой переменной, следовательно:

Э_Б = 0,3.

Теперь определим точку, в которой эластичности по обоим видам продукции одинаковы. Для продукции Б подходит любой объем, т.к. эластичность постоянна, а для определения объема выпуска продукции Б составим и решим уравнение:

= 0,3;

отсюда x_А = 4,3 единиц.

Таким образом, при объеме производства продукции А, равном 4,3, эластичности удельных постоянных расходов обоих видов продукции по объему выпуска одинаковы и равны 0,3.

■

 

Задача 3. Пусть имеется уравнение парной регрессии: y = 5 - 6x + ε, построенное по 15 наблюдениям. При этом r = –0,7.

Определить доверительный интервал, в который с вероятностью 0,99 попадает коэффициент регрессии.

Решение:Для построения доверительного интервала необходимо знать стандартную ошибку m_b коэффициента регрессии. Однако она не задана, и нужно определить ее косвенным путем. Для этого воспользуемся тем, что в парной регрессии существует связь между t- и F-статистиками:

t_b = ,

а F - статистику определим из формулы (19):

F = 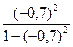· (15-2) = 12,5;

t_b = = –3,53;

(берем минус, так как знак оцененного коэффициента b отрицательный).

m_b = ;

Доверительный интервал имеет вид (t_табл(0,01;13)=3,01):

-6 – 1,7·3,01 < b < -6 + 1,7·3,01

или

-11,11 < b < -0,89.

■

 

Задача 4. Уравнение регрессии потребления материалов от объема производства, построенное по 15 наблюдениям, имеет вид:

y = 5 + 5x + ε

(4,0)

В скобках – фактическое значение t-критерия. Определить коэффициент детерминации для этого уравнения.

Решение: Зная t-критерий для коэффициента регрессии, вычислим F - критерий для данного уравнения:

F = t_b² = 4² = 16.

Далее воспользуемся уравнением (19), из которого определим коэффициент детерминации при n=15:

.

■

 

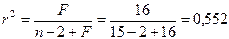Задача 5. По совокупности 18 предприятий торговли изучается зависимость между ценой x на некоторый товар и прибылью y торгового предприятия. При оценке регрессионной модели были получены следующие результаты:

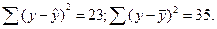
Определить индекс корреляции и фактическое значение F-критерия, а также статистическую значимость уравнения регрессии. Построить таблицу дисперсионного анализа.

Решение: В условиях задачи n=18; остаточная СКО равна 23, а общая СКО – 35. Для расчета индекса корреляции воспользуемся выражением (54):

R = ; R² = 0,343.

 

Фактическое значение F-критерия рассчитаем с помощью выражения (19):

F =

При проверке статистической значимости уравнения в целом воспользуемся F-критерием и сравним его с критическим значением, задавшись уровнем значимости 0,05. Табличное (критическое) значение при этом равно:

F_табл (0,05;1;18-2) = 4,49.

Поскольку фактическое значение, равное 8,35, больше критического, нуль-гипотезу о статистической незначимости уравнения регрессии следует отклонить, и уравнение на уровне α=0,05 является значимым; статистическая связь между y и x считается доказанной. Однако, если задать α=0,01, то:

F_кр = F_табл (0,01;1;16)=8,53,

и в этом случае нуль-гипотезу отклонить нельзя, на уровне α=0,01 уравнение не значимо.

Для построения таблицы дисперсионного анализа определим из балансового уравнения (13) величину факторной СКО:

Поскольку мы имеем дело с парной регрессионной зависимостью, число степеней свободы факторной СКО принимаем равным единице. С учетом этих условий таблица дисперсионного анализа выглядит следующим образом:

Вариация y	СКО	Число степеней свободы	Дисперсия на 1 степень свободы	Fнабл =
Общая			-	-
Факторная				8,35
Остаточная			1,4375

■

Задача 6. Зависимость среднемесячной производительности труда от возраста рабочих характеризуется моделью:

.

Ее использование привело к результатам, представленным в таблице:

№ п/п	Производительность труда рабочих, тыс.руб. (y)	№ п/п	Производительность труда рабочих, тыс. руб. (y)
фактическая	расчетная	фактическая	расчетная

Оценить качество модели, определив ошибку аппроксимации, индекс корреляции и F -критерий Фишера.

Решение: Средняя ошибка аппроксимации рассчитывается по формуле:

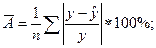
и характеризует среднее отклонение расчетных значений от фактических. Это значение считается приемлемым, если оно не превышает 8-10%.

Для приведенных в таблице данных имеем:

что оказывается в допустимых границах и говорит о приемлемой точности аппроксимации регрессионной модели.

Индекс корреляции рассчитаем по формуле (54), предварительно определив общую и остаточную СКО.

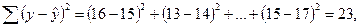
R² =0,425.

F -критерий рассчитаем по формуле (55) с учетом того, что число параметров при переменной x равно двум (зависимость квадратическая, эти параметры – b и c):

Сравним это значение с критическим на уровне 0,05:

,

,

следовательно, уравнение в целом на уровне 0,05 не значимо. Можно предположить, что в исследованном диапазоне строить квадратическую регрессию нецелесообразно. По – видимому, есть смысл упростить уравнение регрессии и описать исходные данные с помощью линейной зависимости.

■

 

Задача 7. Для следующих уравнений регрессии:

а)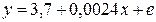

б)

в)

г)

определить коэффициенты эластичности при значении фактора, равном 85.

Решение.

а) Уравнение регрессии является линейным, поэтому коэффициент эластичности равен .

б) Здесь имеем дело с полулогарифмической зависимостью: .

в) Это преобразованная (путем логарифмирования) степенная зависимость; её коэффициент эластичности постоянен и равен показателю степени, т.е. 0,0024.

г) В данном случае зависимость показательная (или экспоненциальная), в преобразованном виде логарифмируется только зависимая переменная. В любой из трех форм записи экспоненциальной регрессии коэффициент эластичности равен произведению коэффициента при факторе на значение самого фактора, т.е. .

■

 

Поделиться:

Воспользуйтесь поиском по сайту: