 |
Список использованных источников
|
|
|
|
Задание 1
Проверить наличие седловых точек в данной матричной игре. Найти решение игры с заданной платежной матрицей А с помощью графического метода, упростив предварительно матрицу игры по принципу доминирования.
.
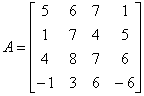Решение
Проверим наличие седловых точек в матрице игры, для этого найдем нижнюю и верхнюю цену игры и сравним их значения. Итак,
соответственно
Так как 
, игра седловой точки не имеет. Теперь упростим матрицу игры, используя принцип доминирования. Для определенности сначала сравним между собой элементы строк и доминируемые строки, если такие имеются, вычеркнем. Итак, все элементы третьей строки строго больше соответствующих элементов второй строки, значит, третья строка доминирует над второй, то есть третья строка является доминирующей, а вторая - доминируемой, поэтому вторую строку вычеркиваем. Аналогично третья строка доминирует над четвертой, значит, вычеркиваем и четвертую строку. Остальные строки не являются доминируемыми или доминирующими. В оставшейся матрице порядка 2´4 сравниваем между собой соответствующие элементы столбцов. Второй и третий столбцы доминируют над первым и четвертым, значит, второй и третий столбцы является доминирующими, а первый и четвертый - доминируемыми, следовательно, вычеркиваем второй и третий столбцы. В результате получаем квадратную матрицу второго порядка, которую больше не упростить:
.
С помощью графического метода найдем решение полученной игры порядка 2´2. Построим графики для первого и второго игроков.
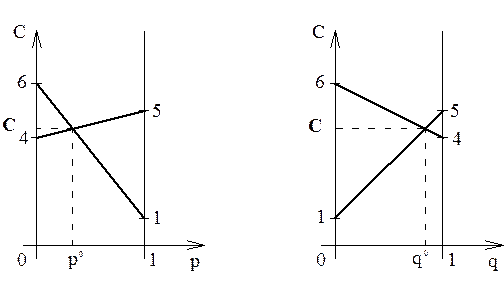
Рисунок 1 – Графики для определения стратегий игроков, цены игры
Сделаем проверку аналитически, для этого нужно решить две системы уравнений; для первого игрока:
|
|
|
Для второго игрока:
Сравнивая найденные значения с графиками, убеждаемся в правильности найденного решения.
Таким образом, цена игры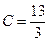 
, а полученные оптимальные стратегии игроков соответственно равны: 
. Нулевые вероятности соответствуют вычеркнутым при упрощении строкам и столбцам.
Ответ: ,.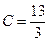 
.
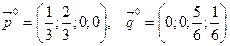Задание 2
Найти цену игры и оптимальные стратегии игроков для заданной матрицы игры Н, предварительно упростив ее по возможности; для решения применить симплекс-метод, составив соответствующую ЗЛП (задачу линейного программирования).
Решение
Сначала упростим платежную матрицу, используя принцип доминирования. Например, вторая строка доминирует над первой, следовательно, первая строка – доминируемая, а вторая – доминирующая, поэтому первую строку вычеркиваем. В оставшейся матрице сравниваем столбцы: первый столбец доминирует над вторым, поэтому является доминирующим, значит, его вычеркиваем. Получаем квадратную матрицу второго порядка, в которой уже ничего не упростить.
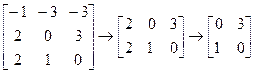
Так как седловой точки нет, решение будем искать в области смешанных стратегий. Составим пару двойственных задач линейного программирования, соответствующих данной матрице игры:
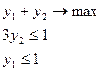
Решение найдем, используя симплекс – метод. Сначала нужно найти решение прямой задачи (вектор 
), а затем по симплексной таблице записать решение двойственной задачи (вектор 
).
В ограничениях перейдем от неравенств к равенствам, для этого введем базисные переменные y 3, y 4:
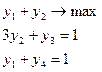
Заполним симплексную таблицу по исходным данным (таблица 1).
Таблица 1 – Итерация №0
| Базисные переменные | Свободные члены | Свободные переменные | |
| - y 1 | - y 2 | ||
| y 3 | 1 | 0 | 3 |
| y 4 | 1 | 1 | 0 |
| Целевая функция | 0 | -1 | -1 |
Так как среди элементов строки целевой функции (не считая свободного члена) имеются отрицательные, решение не является оптимальным. Итак, в качестве разрешающего столбца возьмем второй, тогда разрешающая строка – первая, так как имеем всего одно неотрицательное симплексное отношение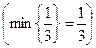 
, таким образом, разрешающий элемент – «3». Используя правила симплексных преобразований, заполним новую симплексную таблицу (таблица 2):
|
|
|
Таблица 2 – Итерация №1
| Базисные переменные | Свободные члены | Свободные переменные | |
| - y 1 | - y 3 | ||
| y 2 | 1/3 | 0 | 1/3 |
| y 4 | 1 | 1 | 0 |
| Целевая функция | 1/3 | -1 | 1/3 |
Так как среди элементов строки целевой функции (не считая свободного члена) имеются отрицательные, решение не является оптимальным. Итак, в качестве разрешающего столбца возьмем первый, тогда разрешающая строка – вторая, так как имеем всего одно неотрицательное симплексное отношение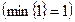 
, таким образом, разрешающий элемент – «1». Используя правила симплексных преобразований, заполним новую симплексную таблицу (таблица 3):
Таблица 3 – Итерация №2
| Базисные переменные | Свободные члены | Свободные переменные | |
| - y 4 | - y 3 | ||
| y 2 | 1/3 | 0 | 1/3 |
| y 1 | 1 | 1 | 0 |
| Целевая функция | 1 1/3 | 1 | 1/3 |
Так как среди элементов строки целевой функции (не считая свободного члена) отрицательных нет, решение прямой задачи найдено – вектор 
. Решение двойственной задачи выписываем из последней симплексной таблицы: свободным переменным y 1, y 2 прямой задачи соответствуют базисные переменные x 3, x 4 двойственной, а базисным переменным y 3, y 4 соответствуют свободные переменные x 1, x 2. Получаем решение двойственной задачи: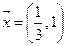 
.
Запишем решение матричной игры: цена игры вычисляется следующим образом - 
, то есть 
. Оптимальные стратегии найдем по формулам: 
, 
.
Нулевые вероятности соответствуют вычеркнутым при упрощении строкам и столбцам. Таким образом, решение игры имеет вид:
Ответ: 
; 
; 
.
Задание 3
Решить матричную игру с платежной матрицей В итерационным методом Брауна с точностью ε=0,3.
Решение
Седловая точка отсутствует, так как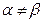 
, действительно
Решение ищем в смешанных стратегиях. Следуя правилам, заполним таблицу метода Брауна, начиная с произвольной стратегии игрока 1, например, с первой.
Таблица 4 – Таблица метода Брауна
| k | i | B 1 | B 2 | B 3 | j | A 1 | A 2 | A 3 |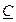 
| 
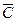
| C* |
| 1 | 1 | -1 | 0 | 1 | 1 | -1 | 1 | 0 | -1 | 1 | 0 |
| 2 | 2 | 0 | -1 | 1 | 2 | -1 | 0 | 1 | -1/2 | 1/2 | 0 |
| 3 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 2 | 1 | -1 | 0 | 2 | 0 | -1 | 1 | -1/4 | 1/4 | 0 |
| 5 | 3 | 1 | 0 | -1 | 3 | 1 | -1 | 0 | -1/5 | 1/5 | 0 |
| 6 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 3 | 0 | 1 | -1 | 3 | 1 | 0 | -1 | -1/7 | 1/7 | 0 |
| 8 | 1 | -1 | 1 | 0 | 1 | 0 | 1 | -1 | -1/8 | 1/8 | 0 |
| 9 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
|
|
|
Итак, сделав достаточное число итераций, запишем смешанные стратегии игрока 1 и игрока 2 (по частоте появления) и цену игры.
Ответ: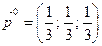 
; 
; 
.
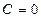Задание 4
Найти полное решение матричной игры с заданной платежной матрицей С, используя метод Шепли-Сноу.
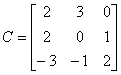
Решение
Находим 
, значит, седловой точки у данной матрицы нет. Запишем все квадратные подматрицы порядка 2´2 и исключим непригодные:
 |  | 
|
 | 
|  |
 | 
| 
|
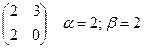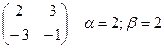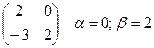
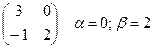
То есть осталось 4 подматрицы порядка 2´2, в которых нужно искать решение.
1 Рассмотрим квадратную подматрицу порядка 3´3, какой является исходная матрица:
.
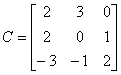Составим соответствующую систему неравенств для нахождения стратегий первого игрока:
Решаем любым известным методом, например, методом Гаусса:
.
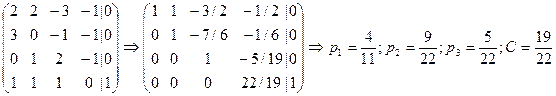Условие неотрицательности выполняется, так как найденные вероятности не отрицательны.
Далее составляем соответствующую систему неравенств для определения стратегии второго игрока и решаем её:
Условие неотрицательности выполняется, потому что полученные вероятности положительны. Таким образом, подматрица дает решение:
; 
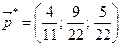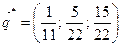
2 Рассмотрим квадратные подматрицы порядка 2´2:
а) Подматрица вида 
Составляем соответствующую систему неравенств и определяем её решение:
Условие неотрицательности выполняется. Проверяем условие оптимальности для вычеркнутого столбца: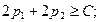 
то есть 
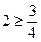верно, соответственно условие оптимальности выполняется.
Далее составляем соответствующую систему неравенств для определения стратегии второго игрока и решаем её:
В найденном решении условие неотрицательности выполняется (найденные вероятности положительны), сделаем проверку условия оптимальности для вычеркнутой строки: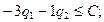 
то есть 
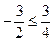верно, соответственно условие оптимальности выполняется. Таким образом, подматрица дает решение:
|
|
|
; 
б) Подматрица вида 
Составляем соответствующую систему неравенств и решаем её:
Условие неотрицательности выполняется (полученные вероятности положительны). Проверяем условие оптимальности для вычеркнутого столбца: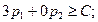 
то есть 
. Условие оптимальности не выполняется. Следовательно, данная подматрица решения не дает.
в) Подматрица вида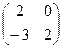 
Составляем соответствующую систему неравенств и находим её решение:
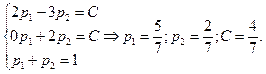
Условие неотрицательности выполняется (найденные вероятности положительны). Проверим условие оптимальности для вычеркнутого столбца: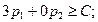 
то есть 
- верно. Условие оптимальности выполняется.
Далее составляем соответствующую систему неравенств для определения стратегии второго игрока и определяем ее решение:
Условие неотрицательности выполняется (найденные вероятности положительны). Проверим условие оптимальности для вычеркнутой строки: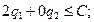 
то есть 
- верно, соответственно условие оптимальности выполняется. Таким образом, подматрица дает решение:
; 
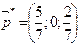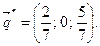
г) Подматрица вида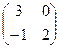 
Составляем соответствующую систему неравенств и находим её решение:
Условие неотрицательности выполняется, так как полученные вероятности положительны. Проверим условие оптимальности для вычеркнутого столбца: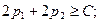 
то есть 
- верно. Условие оптимальности выполняется.
Далее составляем соответствующую систему неравенств для определения стратегии второго игрока и определяем ее решение:
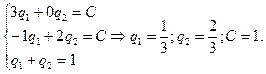
Условие неотрицательности выполняется (найденные вероятности положительны). Проверим условие оптимальности для вычеркнутой строки: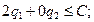 
то есть 
- верно, соответственно условие оптимальности выполняется. Таким образом, подматрица дает решение:
; 
Таким образом, все квадратные подматрицы исследованы на наличие оптимальных крайних стратегий, и можно выписать полное решение исходной игры.
Ответ: 
Задание 5
По предложенной игровой ситуации составить платежную матрицу и найти решение игры с природой.
Магазин «Горячий хлеб» продает в розницу хлебобулочные изделия. Заведующий должен определить, сколько лотков хлеба следует закупать у хлебозавода ежедневно. Вероятности того, что спрос на хлеб в течение дня будет 5, 7, 9 или 10 лотков, равны соответственно 0,45; 0,3; 0,15 и 0,1. Покупка одного лотка хлеба обходится магазину в 50 р., а продается хлеб по цене 95 р. за один лоток. Если хлеб не реализован в течение дня, магазин несет убытки. Определить оптимальную стратегию по количеству приобретенных для продажи лотков хлеба, используя известные критерии: Гурвица (по матрице выигрышей и по матрице рисков), Вальда, Сэвиджа, Лапласа, Байеса-Лапласа, максимаксный критерий.
|
|
|
Решение
Составим платёжную матрицу, используя исходные данные. Стратегиями игрока являются различные показатели числа лотков хлеба, которые ему, возможно, следует закупать. Состояниями природы выступают величины спроса на аналогичное число лотков хлеба. Рассуждая описанным образом, получаем следующую матрицу выигрышей:
| 5 | 7 | 9 | 10 | |
| 5 | 225 | 225 | 225 | 225 |
| 7 | 125 | 315 | 315 | 315 |
| 9 | 25 | 215 | 405 | 405 |
| 10 | -25 | 165 | 355 | 450 |
Вычислим, например, элемент платежной матрицы при закупке 10 лотков хлеба в день, если спрос есть лишь на 7 лотков хлеба. Владелец магазина закупил 10 лотков хлеба, затратив при этом 500 р., а продали лишь 7 лотков хлеба, получив выручку 665 р. Таким образом, прибыль при рассматриваемом сочетании спроса и предложения будет равна 165 р. (разница между выручкой и затратами). Аналогично рассчитываются элементы матрицы игры при других сочетаниях спроса и предложения. Попытки уменьшить размерность матрицы упрощением по принципу доминирования результата не дают.
Найдем оптимальную стратегию по закупке хлеба, применяя известные критерии:
Максиминный критерий Вальда: 
- первая стратегия А 1.
Составим матрицу рисков:
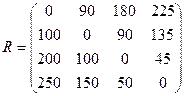
Тогда, применяя критерий Сэвиджа, получим 
, что соответствует выбору стратегии А 2.
Используя критерий Гурвица для матрицы платежей, возьмём р =0,3,
тогда:
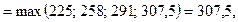
оптимальной является стратегия А 4. Используя же критерий Гурвица для матрицы рисков, имеем:
следовательно, выбираем стратегию А 2.
Критерий Байеса-Лапласа:
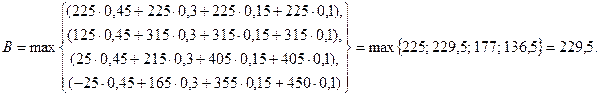
Следовательно, по этому критерию оптимальной будет стратегия А 2.
По максимаксному критерию оптимальной является четвертая стратегия, так как
Таким образом, получаем, что три критерия указывают на стратегию А 2; два критерия – на стратегию А 4 и один критерий на стратегию А 1. Выбор прост, так как, большинство критериев предлагают стратегию А 2.
Ответ: рекомендацией владельцу магазина будет покупка 7 лотков хлеба в день.
Список использованных источников
1. Каверзина С.А. Теория игр: Учебное пособие.– Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2003.– 94 с.
|
|
|
