 |
Задача нахождения неизвестных параметров распределения
|
|
|
|
Задача определения закона распределения случайной величины (или системы случайных величин) по статистическим данным
Мы уже указывали, что закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат больший или меньший элемент случайности. Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности, сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникает характерная для математической статистики задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.
Задача проверки правдоподобия гипотез
Эта задача тесно связана с предыдущей; при решении такого рода задач мы обычно не располагаем настолько обширным статистическим материалом, чтобы выявляющиеся в нем статистические закономерности были в достаточной мере свободны от элементов случайности. Статистический материал может с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы. Например, может возникнуть такой вопрос: согласуются ли результаты эксперимента с гипотезой о том, что данная случайная величина подчинена закону распределения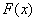 
? Другой подобный вопрос: указывает ли наблюденная в опыте тенденция к зависимости между двумя случайными величинами на наличие действительной объективной зависимости между ними или же она объясняется случайными причинами, связанными с недостаточным объемом наблюдений? Для решения подобных вопросов математическая статистика выработала ряд специальных приемов.
|
|
|
Задача нахождения неизвестных параметров распределения
Часто при обработке статистического материала вовсе не возникает вопрос об определении законов распределения исследуемых случайных величин. Обыкновенно это бывает связано с крайне недостаточным объемом экспериментального материала. Иногда же характер закона распределения качественно известен до опыта, из теоретических соображений; например, часто можно утверждать заранее, что случайная величина подчинена нормальному закону. Тогда возникает более узкая задача обработки наблюдений – определить только некоторые параметры (числовые характеристики) случайной величины или системы случайных величин. При небольшом числе опытов задача более или менее точного определения этих параметров е может быть решена; в этих случаях экспериментальный материал содержит в себе неизбежно значительный элемент случайности; поэтому случайными оказываются и все параметры, вычисленные на основе этих данных. В таких условиях может быть поставлена только задача об определении так называемых «оценок» или «подходящих значений» для искомых параметров, т.е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие. С задачей отыскания «подходящих значений» числовых характеристик тесно связана задача оценки их точности и надежности. Таков далеко не полный перечень основных задач математической статистики. Мы перечислили только те из них, которые наиболее важны для нас по своим практическим применениям. В настоящей главе мы вкратце познакомимся с некоторыми, наиболее элементарными задачами математической статистики и с методами их решения.
|
|
|
Данным, полученным в результате эксперимента, свойственна изменчивость, которая может быть вызвана случайной ошибкой: погрешностью измерительного прибора, неоднородностью образцов и т.д. После проведения большого количества однородных данных экспериментатору необходимо их обработать для извлечения как можно более точной информации о рассматриваемой величине. Для обработки больших массивов данных измерений, наблюдений и т.п., которые могут быть получены при проведении эксперимента, удобно применять методы математической статистики. Математическая статистика неразрывно связана с теорией вероятностей, но между этими науками есть существенное различие. Теория вероятностей использует уже известные распределения случайных величин, на основе которых рассчитываются вероятности событий, математическое ожидание т.д. Задача математической статистики – получить как можно более достоверную информацию о распределении случайной величины на основе экспериментальных данных. Типичные направления математической статистики: теория выборок; теория оценок; проверка статистических гипотез; регрессионный анализ; дисперсионный анализ. Методы математической статистики Методы оценки и проверки гипотез основываются на вероятностных и гиперслучайных моделях происхождения данных. Математическая статистика оценивает параметры и функции от них, которые представляют важные характеристики распределений (медиану, математическое ожидание, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используются точечные и интервальные оценки. Современная математическая статистика содержит большой раздел – статистический последовательный анализ, в котором допускается формирование массива наблюдений по одному массиву. Математическая статистика также содержит общую теорию проверки гипотез и большое количество методов для проверки конкретных гипотез (например, о симметрии распределения, о значениях параметров и характеристик, о согласии эмпирической функции распределения с заданной функцией распределения, гипотеза проверки однородности (совпадение характеристик или функций распределения в двух выборках) и др.). Проведением выборочных обследований, связанных с построением адекватных методов оценки и проверки гипотез, со свойствами разных схем организации выборок, занимается раздел математической статистики, имеющий большое значение. Методы математической статистики непосредственно использует следующие основные понятия. Выборка Определение 1 Выборкой называются данные, которые получены при проведении эксперимента. Например, результаты дальности полета пули при выстреле одного и того же или группы однотипных орудий. Эмпирическая функция распределения Замечание 1 Функция распределения дает возможность выразить все важнейшие характеристики случайной величины. В математической стаитистике существует понятие теоретической (заранее не известной) и эмпирической функции распределения. Эмпирическая функция определяется по данным опыта (эмпирические данные), т.е. по выборке. Гистограмма Гистограммы используются для наглядного, но довольно приближенного, представления о неизвестном распределении. Гистограмма представляет собой графическое изображение распределения данных. Для получения качественной гистограммы придерживаются следующих правил: Количество элементов выборки должно быть существенно меньше объема выборки. Интервалы разбиения должны содержать достаточное число элементов выборки. Если выборка очень большая зачастую интервал элементов выборки разбивают на одинаковые части. Выборочное среднее и выборочная дисперсия С помощью данных понятий можно получить оценку необходимых числовых характеристик неизвестного распределения, не прибегая к построению функции распределения, гистограммы и т.п.
|
|
|
|
|
|
2. Типичные статистические распределения и их параметры
При решении практических задач по надежности и безопасности функционирования сложных систем наиболее широкое применение нашли такие статистические распределения, как биномиальное, нормальное, показательное, пуассоновское, равномерное, а также распределения Стьюдента, Фишера и хи-квадрат, которые используются для аппроксимации различных случайных величин. Ознакомимся с некоторыми из них.
1. Биномиальное распределение относится к дискретным случайным величинам X и рекомендуется для оценки параметров их распределения при испытаниях в практически неизменных условиях, т.е. по так называемой схеме Бернулли. В частности, оно применяется для прогноза вероятности Р(Х = т) появления т случайных исходов в п опытах, в предположении о равной вероятности р возникновения регистрируемого события в каждом из них:
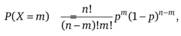(2.24)
где n! и m! – факториалы.
Данное распределение характеризуется двумя числовыми характеристиками: математическим ожиданием т = пр, дисперсией D = nр(1 – р) и используется для интерпретации случайных событий типа отказ или происшествие.
2. Нормальное (Лапласа – Гаусса) распределение названо так из-за большой распространенности и естественной формы графического представления его плотности вероятности (колоколообразная палатка – см. рис. 2.6, б). Это распределение относится только к непрерывным случайным величинам, а его плотность вероятности выражается формулой
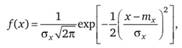(2.25)
где тк, σх – математическое ожидание и стандартное отклонение случайной величины X.
Сфера практического применения данного распределения чрезвычайно разнообразна, в чем можно будет убедиться ниже, например при изучении результатов распространения вредного вещества в атмосфере и прогнозирования остаточного ресурса технических
систем (времени до наступления в них так называемого предельного состояния). А одна из его модификаций (когда тх = 0, σv = 1) названа стандартным нормальным распределением, которое представлено в табличной форме практически во всех литературных и нормативных источниках по теории вероятностей и математической статистике.
3. Показательное, или экспоненциальное, распределение также может иметь лишь непрерывная случайная величинах, и только на отрезке от 0 до +∞. При этом плотность ее вероятности определяется следующим выражением:
|
|
|
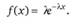(2.26)
Данный тип распределения имеет единственную числовую характеристику λ, обратную величину которой b = 1/λ принято называть параметром масштаба. Оно широко применяется для описания моментов времени отказа сложных технических систем на установившейся стадии их эксплуатации, а также при интерпретации потоков событий, входящих и выходящих из так называемых систем массового обслуживания. Дополнительные и более конкретные сведения, касающиеся уникальной особенности, графического представления и сфер применения экспоненциального распределения, будут изложены несколько ниже (например, см. гл. 3 и 18).
4. Распределение Пуассона (закон редких событий) получается из биномиального при п→∞, Р→0 и когда пР = const. Оно относится к дискретным случайным величинам, позволяя рассчитывать вероятность появления любого наперед заданного количества т каких-то случайных событий по следующей формуле:
(2.27)
где а – единственный параметр этого распределения, являющийся и m, и D.
Наиболее широкое распространение это распределение нашло при количественном описании закономерностей возникновения различных техногенных происшествий на производстве и транспорте, так как их появление в одном и том же месте является сравнительно редким событием, что и подтверждается его названием.
5. Равномерное (прямоугольное) распределение может характеризовать как непрерывную, так и дискретную случайную величину X, а его плотность имеет следующий вид:
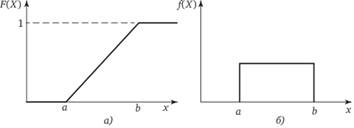
Рис. 2.7. Графики равномерного распределения:
а – функция распределения; б – плотность
где а, b – константы, выбираемые с соблюдением следующего условия: а <х <b.
Данное статистическое распределение является самым неинформативным (обладает максимальной энтропией) и имеет два параметра: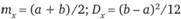 
. Наибольшее распространение равномерный закон нашел при имитационном (статистическом) моделировании с применением цифровой вычислительной техники, где его используют для настройки различных датчиков и генераторов случайных чисел.
Графики плотности и функции распределения для равномерного распределения показаны на рис. 2.7, а пример их практического использования при имитационном моделировании происшествий при функционировании системы "человек – машина – среда" изложен в гл. 11.
Что касается других упомянутых выше распределений, то они описываются более сложными функциональными зависимостями и применяются в качестве вспомогательных соотношений при обосновании решений в интересах менеджмента надежности и техногенного риска, а также для решения ряда задач математической статистики.
3. Связь между экспоненциальным распределением и распределением Пуассона на примере модели чистого рождения.
Модель обслуживающей системы, представленная только поступлением клиентов, называется моделью чистого рождения.
Пусть p0(t) — вероятность отсутствия событий (поступления клиентов) за период времени t. При условии, что длина интервала времени Т между поступлениями клиентов описывается экспоненциальным распределением с интенсивностью λ, будем иметь:
p0(t) = P {интервал времени T ≥ t} = 1 - P {интервал времени T ≤ t} = 1 - (1 - e-λt) = e-λt.
При достаточно малом интервале времени h > 0 имеем:
p0(h) = e-λh = 1 - λh + (λh)2/2! -... = 1 - λh + O(h2).
Экспоненциальное распределение базируется на предположении, что на достаточно малом временном интервале h > 0 может наступить не более одного события (поступления клиента). Следовательно, при h → 0 p1(h) = 1 - p0(h) ≈ λh.
Этот результат показывает, что вероятность поступления клиента на протяжении интервала h прямо пропорциональна h с коэффициентом пропорциональности, равным интенсивности поступлений λ.
Чтобы получить распределение числа клиентов, поступивших на протяжении некоторого интервала времени, обозначим через pn(t) вероятность поступления n клиентов на протяжении времени t. При достаточно малом h > 0 имеем следующее:
pn(t + h) ≈ pn(t)(1 - λh) + pn-1(t)λh, n > 0,
p0(t + h) ≈ p0(t)(1 - λh), n = 0.
Из первого уравнения следует, что поступление п клиентов на протяжении времени t + h возможно в двух случаях: если имеется n поступлений на протяжении времени t и нет поступлений за время h, или существует n - 1 поступлений за время t и одно поступление за время h. Любые другие комбинации невозможны вследствие того, что на протяжении малого периода h возможно наступление только одного события. В соответствии с условием независимости событий к правой части уравнения применим закон умножения вероятностей. Во втором уравнении отсутствие поступлений клиентов на протяжении интервала t + h возможно лишь тогда, когда нет поступлений клиентов за время h. Перегруппировывая члены и переходя к пределу при h → 0, получаем следующее. Решение приведенных выше разностно-дифференциальных уравнений имеет следующий вид: В данном случае мы получили дискретную плотность вероятности распределения Пуассона с математическим ожиданием M{n | t} = λt поступлений за время t. Дисперсия распределения Пуассона также равна λt. Полученный результат означает, что всякий раз, когда временные интервалы между моментами последовательных поступлений заявок распределены по экспоненциальному закону с математическим ожиданием 1/λ, число поступлений заявок в интервале, равном t единиц времени, характеризуется распределением Пуассона с математическим ожиданием λt. Верным является и обратное утверждение. Соответствие между экспоненциальным распределением (с интенсивностью поступлений λ) и распределением Пуассона показано в следующей таблице.
Таблица 1. Соответствие между экспоненциальным распределением и распределением Пуассона
| Экспоненциальное распределение | Распределение Пуассона | |
| Случайная переменная | Время t между наступлениями событий | Количество n наступлений событий в течение заданного периода времени T |
| Значение случайной величины | t ≥ 0 | n = 0, 1, 2,... |
| Функция плотности вероятности | f(t) = λe-λt, t ≥ 0 | pn(t)=(λt)ne-λt/n!, n = 0, 1, 2,... |
| Среднее значение (математическое ожидание) | 1/λ временных единиц | λT в течение времени T |
| Функция распределения | P(t ≤ A) = 1 - e-λA | pn ≤ N(T) = p0(T) + p1(T) +... + pN(T) |
| Вероятность, что не произойдет ни одного события в течение времени A | P(t > A) = e-λA | p0(A) = e-λA |
4. Закон больших чисел
Под законом больших чисел в широком смысле принято понимать общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Или иначе: При большом числе случайных величин их средней результат перестает быть случайным и должна быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле принято понимать ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенство Чебышева: для любой случайной величины, имеющей математическое ожидание M (X) и дисперсию D (X) справедливо:
, (4.1)
или
,(4.2)
В случае если формула (6.1) устанавливает верхнюю границу рассматриваемого события, то (4.2) – нижнюю границу вероятности события, состоящего в том, что отклонения значения случайной величины от математического ожидания не превысит (не будет менее) величины, где – достаточно малая величина.
В приложении к выборочному методу неравенство Чебышева должна быть сформулировано так: при неограниченном увеличении числа наблюдений () в генеральной совокупности с ограниченной дисперсией с вероятностью близкой к единице можно ожидать, что отклонение выборочной средней () от генеральной средней будет сколь угодно мало: при. Эту вероятность в теореме А.М. Ляпунова (1901ᴦ.) используют для определœения ошибки наблюдений.
, (4.3)
где - нормированная формула Лапласса.
– средняя квадратическая или стандартная ошибка выборки.
. (4.4)
Пусть нужно измерить некоторою величину, истинное значение которой равно a. Пусть результат каждого измерения – случайная величина Xi (i =1,2,…, n). В случае если при измерениях отсутствует систематические погрешности, то M (Xi)= a при любом i. Тогда средняя арифметическая результатов и измерений сходится по вероятности к истинному значению a.
(4.5)
Дисперсия средней случайной величины Xi равна
(4.6)
Среднее квадратическое отклонение ошибок выборки
, (4.7)
. (4.8).
Зная выборочную среднюю и предельную ошибку выборки можно определить границы, в которых размещена генеральная средняя.
Величина средней квадратической ошибки простой случайной повторной выборки должна быть определœена по формуле:
, (4.9)
ᴛ.ᴇ. чем больше вариация признака в генеральной совокупности, тем больше ошибка выборки.
Величину называют предельной ошибкой для определœения значения вероятности. В случае если требуется оценить среднюю генеральной совокупности с вероятностью 0,9545, то нужно получить значение выборочной средней из соотношения (функция Лапласа).
Для выборки объёма предельная ошибка должна быть определœена из соотношения.
| t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
| F(t) | 0,683 | 0,9500 | 0,9545 | 0,9901 | 0,9973 |
- ϶ᴛᴏ предел возможной ошибки (правило ʼʼтрех сигмʼʼ).
Формула предельной ошибки выборки используется не только для оценки пределов, в которых находится изучаемый признак в генеральной совокупности, но и для определœения крайне важно го объёма выборки при заданной ее ошибке. Третий тип задач, которые бывают решены с использованием предельной ошибки выборки, - ϶ᴛᴏ определœение вероятности, с которой можно гарантировать, что ошибка выборки не выйдет за заданные пределы. Величина дисперсии генеральной совокупности принципиально не известна и можно говорить лишь о ее оценке по результатам одной выборки.
–для простой случайной выборки.
При, поправка становится 3,5% (30/(30-1)), в связи с этим ею можно пренебречь.
Контрольные вопросы и вопросы для самостоятельной работы:
1. Какие виды типовых статистических распределений вам известны?
2. Какова связь между пуассоновским и экспоненциальным распределениями?
3. Охарактеризуйте особенности нормального распределения.
4. Каким требованиям должна удовлетворять выборочная совокупность?
5. Что принято понимать под законом больших чисел?
6. Место теоремы Бернулли в оценивании категории теории вероятностей?
7. Какую числовую характеристику позволяет оценить теорема Чебышева?
8. Какую роль в математической статистике играет центральная предельная теорема?
9. Перечислите типы задач, решаемых методами математической статистики.
10. Какие типы статистических гипотез вам известны?
11. Чем отличается последовательный анализ статистических гипотез от классического?
12. Поясните ошибки, связанные с проверкой статистических гипотез.
Список источников:
1. http://scask.ru/a_book_tp.php?id=29
2. http://spravochnick.ru/matematika/metody_matematicheskoy_statistiki
3. http://www.aup.ru/books/m163/1_2_4.htm
4. https://studme.org/1673042624523/menedzhment/tipichnye_statisticheskie_raspredeleniya_parametry
5. https://www.stud24.ru/statistics/svyaz-jeksponencialnogo-raspredeleniya-s-raspredeleniem/125837-369483-page2.html
6. http://referatwork.ru/category/matematika/view/143614_zakon_bol_shih_chisel_i_predel_nye_teoremy
7. С.М. Васин, В.С. Шутов «УПРАВЛЕНИЕ РИСКАМИ НА ПРЕДПРИЯТИИ»
8. РУКОВОДСТВО ПО ОЦЕНКЕ ПРОФЕССИОНАЛЬНОГО РИСКА ДЛЯ ЗДОРОВЬЯ РАБОТНИКОВ.
ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ ОСНОВЫ, ПРИНЦИПЫ
И КРИТЕРИИ ОЦЕНКИ
|
|
|
