 |
Теорема 2.5. О производной обратной функции
|
|
|
|
Глава 4.
Тема. 2 Дифференцирование сложной функции. Цепное правило.
Определение 2.1 Пусть переменная 
является аргументом функции 
. В свою очередь 
сама является функцией от аргумента 
. Тогда функция 
называется функцией от функции или сложной функцией.
Пример 2.1. Пусть 
. Тогда 
. Пусть 
, а 
. Тогда 
.
Непрерывность функции от функции.
Напомним определение непрерывной в точке 
функции.
Определение 2.2. Функция 
Теорема 2.1. Любая функция, дифференцируемая в точке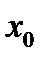 
, будет непрерывной в точке .
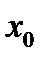Доказательство. 
Следовательно
Теорема 2.2. О непрерывности сложной функции в области. Обозначим область задания
функции 
через 
, а область её значений 
. Тогда, если функция непрерывна
на множестве 
, а функция 
непрерывна на множестве , то сложная функция 
будет непрерывна на множестве .
Дифференцируемость сложной функции
Следующая теорема показывает, что если функции, из которых состоит сложная функция, дифференцируемы, то и сама сложная функция дифференцируема, причем её производная равна произведению производных, формирующих эту сложную функцию.
Теорема 2.3. Правило дифференцирования сложной функции. Цепное правило.
Пусть 
имеет производную в точке 
: 
. Функция имеет производную в
точке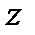 
: 
. Тогда производная сложной функции 
вычисляется по правилу
(2.1)
Замечание. Производная 
означает следующее. Сначала вычисляется производная по переменной 
, а затем вместо переменной 
подставляется функция 
.
Правило вычисления производной сложной функции (2.1) будем для простоты называть цепным правилом.
Доказательство теоремы. Рассмотрим точку 
, в окрестности которой функции 
и дифференцируемы. Поскольку любая дифференцируемая функция непрерывна, то функции 
и непрерывны в этой окрестности. По теореме 2.2 сложная функция тоже непрерывна в этой окрестности. Пусть 
Рассмотрим ненулевые приращения, то есть если 
. Это справедливо, например, для строго монотонных функций. Заметим, что если 
, то по непрерывности 
. Приращение сложной функции будет таким
|
|
|
(2.2)
Докажем формулу (2.1)
1 шаг. Вычисляем отношение приращений
(2.3)
2 шаг. Чтобы вычислить производную, переходим к пределу в выражении (2.3)
Теорема доказана.
Замечание. В общем случае доказательство теоремы можно найти в любом учебнике по математическому анализу.
Пример 2.2. Вычислить производные следующих функций
1) 
2) 
3) 
4) 
Решение. Решаем 1) 
Решаем 2) 
Решаем 3) 
Решаем 4) 
Замечание. Сложная функция может состоять из любого числа базовых функций (звеньев).
Пример 2.3. По заданным сложным функциям найти их базовые составляющие
Решение.
Решаем 1)
Решаем 2)
Решаем 3).
Производная вычисляется по тому же цепному правилу с той лишь разницей, что количество сомножителей в формуле (3.1) увеличивается.
Пример 2.4. Вычислить производную функции 
. Решение. 
Обратная функция и её дифференцирование.
Связь между производными прямой и обратной функциями в общем случае
Пусть заданы две взаимно обратные функции 
:
А.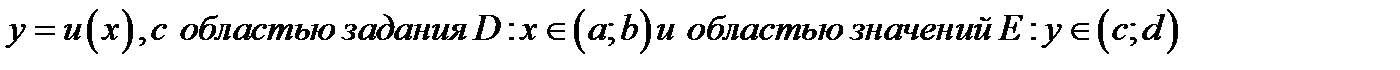 
и
В. 
Тогда для функции от функции справедливо тождество 
. Дифференцируя обе части по аргументу 
, получаем, используя цепное правило
(2.4)
Теорема 2.5. О производной обратной функции
Если 
и 
две взаимно обратные функции. То их производные связаны между собой равенствами
(2.5)
Доказательство. Следует из формулы (2.4).
Как пример рассмотрим вычисление производных обратных тригонометрических функций
Хорошо известно, что функции 
являются взаимно обратными и для них справедливо тождество
. (2.6)
Нам нужно получить формулу вычисления производной по аргументу 
: 
.
|
|
|
Вычисляя производную по аргументу 
от обеих частей тождества, получаем, применяя цепное правило в левой части равенства 
.
Отсюда 
В последнем равенстве мы воспользовались формулами
|
|
|
