 |
Особенности волноводного распространения
|
|
|
|
Принципы работы волоконно-оптических систем передачи
Волноводное распространение
Оптические явления на границе раздела двух сред
волоконный оптический связь волновод
В основе волноводного распространения света лежит эффект полного внутреннего отражения. Этот эффект наблюдается тогда, когда свет проходит из более плотной оптической среды в менее плотную. Закон Снеллиуса 
дает угол полного внутреннего отражения 
.
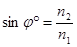Коэффициент преломления
Т=I1/I2,
где I1 и I2 - интенсивности преломленного и падающего света соответственно. Коэффициент отражения
R=I1/I2,
где I1 и I2 - интенсивности отраженного и падающего света соответственно. R+T = 1 при отсутствии потерь.
Поляризацией света называют направление колебания вектора Е.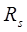 
- вектор Е перпендикулярен плоскости прохождения луча. 
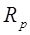- вектор Е параллелен плоскости прохождения луча.
Е-перпендикулярная волна
Е-параллельная волна
Прохождение света из менее плотной среды в более плотную.
Е-перпендикулярная волна
Е-параллельная волна
Прохождение света из более плотной среды в менее плотную. На этом графике показан угол полного внутреннего отражения.
Так же на обоих графиках показан угол Брюстера, при котором коэффициент отражения Е-параллельной волны равен нулю.
При нормальном падении света
= = 
.
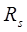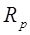Полное внутреннее отражение
В условиях полного внутреннего отражения на границе двух сред световая волна не отражается в одной точке. Волна выступает за границу раздела сред на расстояние ∆х (явление сдвига Гуса-Генхе). Расстояние ∆х определяется как расстояние от поверхности раздела сред, на котором вектор волны Е угасает в е раз.
|
|
|
Е=Е0 
, где α - коэффициент затухания
α= 
Отраженная волна испытывает фазовый сдвиг.
Оптические волноводы
Возможность распространения света в волокне обусловлена эффектом полного внутреннего отражения, чтобы обеспечить полное внутреннее отражение, необходимо добиться того, чтобы n световода был больше n подложки.
Для волноводов с толщиной h больше λ применимы законы геометрической оптики. Для волноводов с толщиной h ≈ λ применимы законы волновой оптики.
Характеристическое уравнение волнового распространения в волноводе имеет вид
∆ φ(n')=δh-δ13-δ12=2πm (m=1,2,3….)
Это уравнение решается графическими или числовыми методами.
Решение характеристического уравнения - дискретные значения углов. Физический смысл дискретных решений - дискретные углы, при которых возможно распространение волны.
постоянная распространения.
N (m)= β(m)⁄к - волноводный показатель преломления
V (m)= N (m)⁄с - скорость волны в волноводе
| m | 0 | 1 | 2 | 3 | 4 | … |
| Φ(m) | Φ₀ | Φ₁ | Φ₂ | Φ₃ | Φ₄ | … |
| β(m) | β ₀ | β ₁ | β ₂ | β ₃ | β ₄ | … |
| N(m) | N ₀ | N ₁ | N₂ | N ₃ | N ₄ | … |
| V(m) | V₀ | V₁ | V₂ | V₃ | V₄ | … |
Волновая мода - особый тип волны, который при фиксированном значении угла φ может распространяться в данном волноводе. Для планарного волновода различают два типа волн: ТМm и ТЕm - Е-параллельная и Е-перпендикулярная соответственно, m - индекс моды. Индекс моды определяет количество узлов в волне в поперечном сечении среды распространения.
Особенности волноводного распространения
1. Электромагнитная волна распространяется по волноводу, приобретая дискретную пространственную структуру (волноводные моды).
2. Волновая мода (любая) имеет нелинейную дисперсионную зависимость.
Условия волноводного распространения (УВР).
|
|
|
βm=nвksinφm 1) nпk < βm < nвk
βmmax=nвk Nm=βm/k=nвsinφm
βmmin=nвksinφ=nпk 2) nп < Nm < nв
Nm - эффективный волноводный показатель преломления.
Vп > Vm > Vв
Из УВР 2 следует, что мода движется в среде со своим индивидуальным показателем преломления Nm, который должен быть меньше показателя преломления волновода и больше показателя преломления подложки.
Левая часть УВР: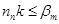 
, 
, 
- нарушение левой части приводит к нарушению ПВО и свет проникает в смежную среду.
Правая часть УВР: 
, 
, 
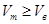- принципиальный запрет на скорость моды меньше скорости в волноводе.
Дисперсионная зависимость для волнового процесса это функциональная связь между пространственными и временными переменными электромагнитной волны.
k=2π/λ=ω/c - пространственная характеристика волны
ω=2πt, ω=ck - временные характеристики волны.
Нелинейная дисперсионная зависимость световой волны в световоде выражается как Е=Е0Sin (ωt-kz).
Примерный график нелинейной дисперсионной зависимости от постоянной распространения β.
При ω→0 Vфаз→Vп.
При ω→∞ Vфаз→Vв.
Нормированная переменная
I)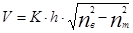 
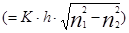Нормированная частота
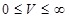
II) 
(
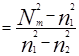) Нормированный показатель преломления
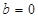!!! Критическое условие
III) 
Степень ассиметрии
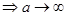
Характеристическое уравнение в нормированных переменных имеет вид
Критическое условие: 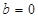и nпk=β
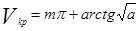
Если волновод симметричный, то 
Количество мод в волноводе определяется по формуле 
Критическое условие W=0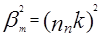 
|
|
|
