 |
Нахождение параметров тренда
|
|
|
|
Поиск тренда следует производить исходя из данного выше определения, что он является непериодической систематической составляющей. Это означает, что в качестве тренда не следует использовать полиномы, особенно высоких степеней, как, например, в [1]. Кроме того, очень важно учитывать экономическую природу временного ряда. Под этим понимается то, что поскольку объектом исследования является объём продаж товара на разных стадиях его жизненного цикла, то тренд должен изначально учитывать основные закономерности динамики. Так, вполне очевидно, что в качестве тренда не годится экспоненциальная функция, даже если временной ряд отражает бурный рост продаж нового товара. В прогнозной части этот рост неизбежно начнёт тормозиться. Исходя из этого, наиболее подходящей функцией для описания тренда является логарифм, даже если он будет иметь более низкий коэффициент детерминации, чем иные функции.
На рисунке 1 приведены регрессии временного ряда, построенные с использованием различных функций. Экспоненциальная регрессия имеет больший коэффициент детерминации, чем логарифмическая, однако очевидно, что для прогноза она никак не годится. Наибольший коэффициент детерминации имеют степенная и квадратичная регрессии, которые в данном случае получились близкими к линейной. В результате они не отражают неизбежного торможения роста продаж. Даже если оно произойдёт не в ближайший период-два, логарифмическая регрессия всё равно выглядит предпочтительной, хотя и имеет наименьший коэффициент детерминации среди всех представленных. Исходя из приведённых рассуждений, для поиска тренда будет использована логарифмическая регрессия:
|
|
|
 . (2)
. (2)
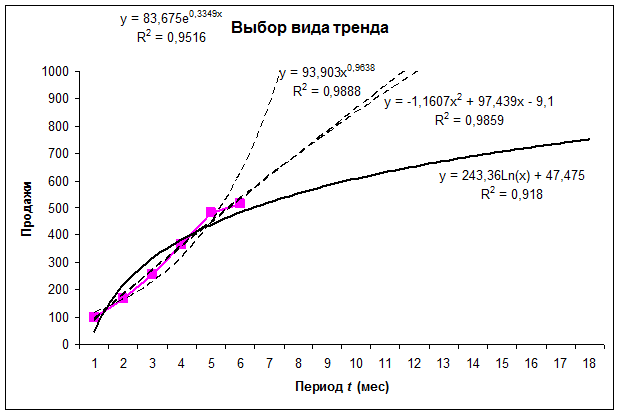 Рисунок 1. Демонстрация различных регрессий для одинаковых исходных данных (ряд с квадратными маркерами, отражающих динамику продаж некоторого товара.
Рисунок 1. Демонстрация различных регрессий для одинаковых исходных данных (ряд с квадратными маркерами, отражающих динамику продаж некоторого товара.
В качестве объекта исследования для определения темпа роста и прогнозного объёма продаж взят временной ряд с помесячными данными за 2 года. На рисунке 2 исходный ряд имеет квадратные маркеры. В нём явно присутствует сезонность с выраженным низким сезоном в первом полугодии и ростом объёмов продаж во втором полугодии. Получается, что сезонный рост от января к декабрю неизбежно попадает в регрессию, хотя к среднегодовому росту не имеет отношения. Действительно, логарифмическая регрессия, построенная по исходному ряду, имеет более высокие темпы среднегодового роста, чем исходные данные.
Для того чтобы регрессия соответствовала тренду годового роста, из исходного временного ряда предварительно должна быть удалена сезонность. Традиционно эта задача решается методами сглаживания исходного ряда или подбором начала и окончания временного ряда, но такие методы не приводят к гарантированному результату [3]. В идеале для правильного нахождения сезонности из исходного ряда должен быть удалён тренд. Разорвать этот заколдованный круг можно, только решая задачи выделения тренда и сезонности одновременно.

Рисунок 2. Выделение тренда и построение прогноза по исходному временному ряду
Для начала ответим на вопрос, каким образом можно «засечь» присутствие тренда. На рисунке 3 схематично представлен временной ряд, содержащий только сезонность и тренд за 3 года по месяца, где года идут друг за другом. Проделаем с этим графиком следующую манипуляцию: отразим года не друг за другом, а выровняем их по первому месяцу (см. рис. 4). Каким образом присутствие тренда выдаёт себя? Из-за тренда кривые продаж лежат одна над другой. Если ту же манипуляцию проделать предварительно элиминировав тренд, то графики продаж по годам просто бы совпали.
|
|
|
 Рисунок 3. Схематическое представление временного ряда с трендом и сезонностью без случайной компоненты.
Рисунок 3. Схематическое представление временного ряда с трендом и сезонностью без случайной компоненты.

Рисунок 4. График с рисунка 3 с наложением годовых отрезков друг на друга горизонтальным сдвигом
Реальный же исходный временной ряд помимо тренда и сезонности содержит случайную составляющую и, возможно, другие системные составляющие. Поэтому при выравнивании периодов годовые графики при удалении тренда совпадать, конечно же, не будут. Однако, если использовать меру расстояния между наложенными графиками, то при правильном элиминировании тренда она должна принять минимально возможное значение. Расстояние между наложенными годовыми отрезками назовём невязкой. В качестве меры расстояния можно принять любую положительно определённую функцию, поскольку важно его абсолютное значение.
В таблице 1 приведён пример расчёта невязки. Для её вычисления предварительно необходимо получить значения исходного временного ряда без тренда  . На момент вычисления параметры тренда могут быть произвольными. Величина невязки рассчитывается попарно для каждых двух годовых отрезков r и s:
. На момент вычисления параметры тренда могут быть произвольными. Величина невязки рассчитывается попарно для каждых двух годовых отрезков r и s:
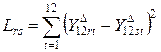 . (3)
. (3)
В данном случае в качестве меры расстояния взята квадратичная функция. Практика применения метода показала её преимущество перед линейной функцией, поскольку она сильнее штрафует большие отклонения. Для нахождения тренда необходимо решить задачу минимизации суммарной невязки по всем годовым отрезкам:
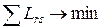 , (4)
, (4)
изменяя параметры тренда, в данном случае это переменные a и b функции (2). Тренд, полученный в результате решения этой задачи, и будет искомым наилучшим трендом среди всех возможных. Решение всегда существует, поскольку 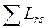 является выпуклой функцией.
является выпуклой функцией.
В таблице 1 решение задачи получено с помощью функции «Поиск решения» MS Excel. Результат графически представлен на рисунке 2. Видно, что искомый тренд имеет гораздо меньшее значение параметра a, чем регрессия, построенная по исходному ряду: a= 106 у тренда (см. внизу табл. 1) против a= 213,7 у регрессии (см. рис. 2).
Таблица 1. Пример расчётов по изложенной методике для одного товара с использованием логарифмического тренда, тыс. руб.
|
|
|
| Период, номер | Период, наименование | Продажи, тыс.руб. | Прогноз | Тренд | Ряд без тренда | Невязка | Сезонность |
| t | Yt | YtТр+YtСез | YtТр | Yt-YtТр | Lrs | YtСез | |
| январь_1 | 126 206 | ||||||
| февраль | 201 379 | -131 | |||||
| март | -200 | 234 061 | |||||
| апрель | 1 691 | ||||||
| май | -172 | 15 360 | -110 | ||||
| июнь | 1 036 | 47 791 | |||||
| июль | 1 364 | 1 015 | 487 508 | ||||
| август | 1 782 | 1 506 | 302 836 | ||||
| сентябрь | 1 306 | 1 387 | 25 816 | ||||
| октябрь | 1 131 | 1 295 | 106 980 | ||||
| ноябрь | 1 645 | 1 535 | 48 452 | ||||
| декабрь | 1 187 | 1 320 | 70 955 | ||||
| январь_2 | 1 344 | 1 167 | |||||
| февраль | -355 | -131 | |||||
| март | 1 224 | ||||||
| апрель | 1 081 | 1 061 | |||||
| май | -48 | -110 | |||||
| июнь | 1 043 | -26 | |||||
| июль | 1 121 | -193 | |||||
| август | 1 328 | 1 603 | |||||
| сентябрь | 1 557 | 1 476 | |||||
| октябрь | 1 542 | 1 378 | |||||
| ноябрь | 1 503 | 1 613 | |||||
| декабрь | 1 526 | 1 393 | |||||
| январь_3 | 1 236 | ||||||
| февраль | -131 | ||||||
| март | 1 044 | 1 002 | |||||
| апрель | 1 120 | 1 006 | |||||
| май | 1 009 | -110 | |||||
| июнь | 1 097 | 1 013 | |||||
| июль | 1 172 | 1 016 | |||||
| август | 1 653 | 1 020 | |||||
| сентябрь | 1 524 | 1 023 | |||||
| октябрь | 1 424 | 1 026 | |||||
| ноябрь | 1 657 | 1 029 | |||||
| декабрь | 1 436 | 1 032 | |||||
| Сумма год 1 | 13 105 | 12 917 | Параметры тренда | ||||
| Сумма год 2 | 14 292 | 14 481 | a = | ||||
| Сумма год 3 | 15 129 | b = |
|
|
|


