Нелинейные эффекты в волоконной оптике

При взаимодействии электромагнитной волны со связанными электронами диэлектрика отклик среды зависит от оптической частоты w. Это свойство, называемое хроматической дисперсией, проявляется как частотная зависимость показателя преломления n(w). Возникновение хроматической дисперсии связанно с характерными частотами, на которых среда поглощает электромагнитное излучение вследствие осцилляций связанных электронов. Вдали от резонансных частот среды поведение показателя преломления хорошо описывается уравнением Селлмейера.

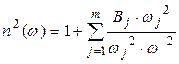, (1.37)

где w_j - резонансная частота,

B_j – величина j-ого резонанса.

Суммирование в уравнении (1.37) производится по всем резонансным частотам вещества. В случае оптических волокон параметры w_j и B_j определяются путем подгонки измеренных дисперсионных критериев к уравнению (1.37) при m=3. Для объемного кварцевого стекла, эти параметры приведены в работе.

Дисперсия в волоконном световоде имеет определяющее значение при распространении коротких оптических импульсов, так как различные спектральные компоненты спектра импульса распространяются с разными скоростями c/n(w). Данное явление, известное как дисперсия групповых скоростей (ДГС) приводит к дисперсионному уширению волнового пакета. Параметр ДГС, b₂, определяющий уширение импульса, связан с дисперсионным параметром волокна D следующим выражением , где 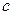скорость света и l длина световой волны. Поскольку хроматическая дисперсия связана с различием групповых скоростей разных спектральных компонент светового сигнала, то величина уширения импульса DТ пропорциональна не только длине волокна L, но и ширине спектра источника излучения оптического сигнала Dl. В результате выражение ВL|D|Dl<1 определяет ограничение скорости передачи битов из-за ДГС. Для обеспечения высокой скорости передачи величина DТ должна быть минимально возможной.

Влияние дисперсии обычно снижается за счет выбора значения несущей длины волны вблизи нулевой дисперсии. Однако использование больших длин волн и более мощных лазерных источников сигнала или же оптических усилителей (ОУ) с мощными источниками накачки приводит к резкому возрастанию влияния нелинейных эффектов.

С теоретической точки зрения возникновение нелинейного отклика связанно с ангармоническим движением связанных электронов при воздействии приложенного поля . В результате индуцированная поляризация 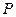, так как не является линейной удовлетворяет более общему соотношению

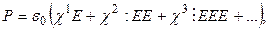(1.38)

где - диэлектрическая проницаемость вакуума;

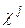- восприимчивость j-ого порядка.

Главный вклад в 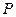вносит линейная восприимчивость 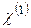. Она определяет показатель преломления и постоянную затухания 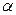. С восприимчивостью второго порядка 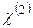связаны такие эффекты, как генерация второй гармоники и генерация суммарной частоты. Однако эта восприимчивость ненулевая только для сред, в которых молекулярном уровне отсутствует симметрия инверсии. Для кварцевого стекла из-за его симметрии на молекулярном уровне она нулевая. Нелинейные эффекты низшего порядка в оптических световодах возникают из-за восприимчивости третьего порядка.

Существует два вида нелинейных явлений, которые необходимо учитывать в современных линиях связи. Явления, которые связаны с зависимостью показателя преломления волокна от оптической мощности. К ним относятся:

a) фазовая самомодуляция (SPM – Self-Phase Modulation);

b) перекрёстная фазовая модуляция (XPM – Cross-Phase Modulation).

c) интермодуляция, модуляционная нестабильность (IM – Inter Modulation);

d) четырехволновое смешение (FWM – Four Wave Mixing);

Явления, которые связаны с эффектом рассеивания световой волны в волокне и в свою очередь вызваны вынужденным рассеиванием Бриллюэна (SBS – Stimulated Brillouin Scattering) и вынужденным рамановским рассеиванием (SRS – Stimulated Raman Scattering).

Эффекты нелинейного преломления. Первая группа нелинейных эффектов, обязана изменению величины рефракционного индекса (иначе показателя преломления) n в зависимости от оптической мощности, проходящей по волокну. Рефракционный индекс твердого кристаллического материала (в ОВ наиболее часто используется кварц) выражается формулой:

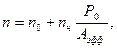(1.39)

где n₀ – индекс рефракции сердцевины ОВ при малых уровнях оптической мощности (для кварца n₀»1,47);

n_н – коэффициент нелинейности рефракционного индекса, величина которого лежит в пределах 2,2…3,6*10^-20 м²/Вт (для традиционного кварца, используемого в ОВ n_н =2,35*10^-20 м²/Вт). Не смотря на малость такого коэффициента, он оказывает очень существенное влияние на нелинейные эффекты в ОВ;

Р₀ – оптическая мощность, передаваемая по ОВ в Вт;

А_эфф – эффективная площадь ядра ОВ в м².

Из выражения (1.39) видно, что для поддержания постоянства индекса рефракции nнеобходимо использовать ОВ с максимально возможной величиной эффективной площади сечения А_эфф. Именно данной проблеме посвящены усилия разработчиков ОВ. Дело в том, что геометрическая площадь сечения волокна с D₁=10 мкм: S=pD₁/4=78,5 мкм². Распределение же оптической мощности в поперечном сечении ОВ не равномерно, а имеет вид гауссовой кривой. По этой причине эффективный диаметр модового пятна (D_эфф) меньше геометрического. Например, для стандартного одномодового ОВ с D₁=10 мкм диаметр модового пятна равен примерно 4 м, а эффективная площадь А_эфф=50 мкм², то есть в 1,5 раза меньше геометрической. С помощью подбора легирующих добавок и формы профиля показателя преломления, эффективную площадь А_эффудается существенно увеличить. Так, известная компания Corning разработала волокно LEAF, имеющее А_эфф=7,25 мкм², а японская фирма Fujikura создала одномодовое волокно с А_эфф=165 мкм², сохранив в норме остальные важные характеристики ОВ: хроматическую дисперсию 20,5 пс/нм ·км и погонное затухание 0,205 дБ/км.

Именно применение новых типов одномодовых ОВ позволило в последних разработках систем DWDM вводить в нелинейное волокно суммарную оптическую мощность группового сигнала порядка +30 dBm (то есть. 1 Вт). В таких системах использованы ОВ не только с большой площадью А_эфф, но и с повышенной очисткой кварца, в результате чего на длине волны 1550 нм получен коэффициент затухания a=0,151 дБ/км (при теоретическом минимуме 0,14 дБ/км).

На рисунке 1.15 показана зависимость рефракционного индекса от оптической мощности в кварце. Из графика видно, что изменение рефракционного индекса незначительно по своей величине. Тем не менее, даже такое изменение рефракционного индекса nоказывает существенное влияние на качество передачи высокоскоростных потоков на протяженных ВОЛП.

Рисунок 1.15 - Зависимость рефракционного индекса кварца от оптической мощности

Фазовая самомодуляция (ФСМ), (SPM – Self-Phase Modulation) возникает из-за нелинейный эффект Керра. Эффект Керра заключается в том, что импульсы, начиная с некоторого уровня интенсивности, распространяются с различными скоростями, зависящими от интенсивности. Явление SPM рассматривается, в основном, применительно к цифровым ВОЛП, работающим на высоких скоростях (например, 2,5 Гбит /с), то есть при малых длительностях импульсов (менее 200…400 пс). SPM начинает проявляться в ОВ при мощностях, более 8…10 мВт и не зависит от частотной канальной расстановки или числа каналов. Указанный выше порог условен, так как он значительно зависит от типа ОВ.

Известно, что спектр импульса связан с его длительностью и, особенно, с крутизной переднего и заднего фронтов. Согласно обратному преобразованию Фурье, передний фронт обязан высокочастотным составляющим в спектре сигнала (то есть более коротким длинам волн), а задний фронт – низкочастотным составляющим. Данное распределение иллюстрируется рисунком 1.16.

Рисунок 1.16 – Связь спектральных составляющих с формой сигнала

При прохождении оптического импульса вдоль ОВ меняется его амплитуда. Следовательно, изменяется и величина рефракционного индекса n, зависящего от интенсивности света в конкретном сечении по длине волокна. Мощность импульсного сигнала можно рассматривать как временную функцию, то есть изменение энергии сигнала во времени. В соответствии с изменением интенсивность оптического света (I) по времени, будет меняться и индекс рефракции:

(1.40)

После прохождения импульсом с несущей частотой w₀ определенного расстояния L, неизбежно произойдет изменение его фазы:

(1.41)

где d_n – изменение величины рефракционного индекса.

Величина рефракционного индекса может быть как положительной, так и отрицательной:

(1.42)

Следует отметить, что энергия импульса минимальна на его переднем фронте и максимальна на заднем фронте. Поэтому изменение величины рефракционного индекса (то есть спектра и формы сигнала) будет претерпевать максимальные изменения именно на заднем фронте импульса, сильно искажая его форму (но не саму длительность). Отсюда вытекает и само название данного вида искажений – “фазовая самомодуляция”. На рисунке 1.17 представлены осцилляции на заднем фронте импульса за счет ФСМ/SРM.

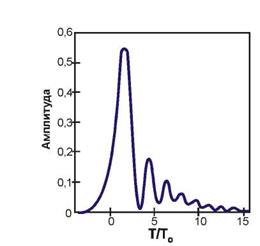
Рисунок 1.17 – Осцилляции на заднем фронте импульса, вызванные ФСМ

Так как частота в математическом представлении представляет собой производную фазы по времени 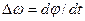, то сам импульс оказывается промодулированным не только по амплитуде, но и по частоте:

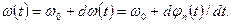(1.43)

Эффект кратковременного изменения несущей частоты называется чирпированием по частоте (см. рисунок 1.18). При n_н>0 наблюдается понижение частоты, а при n_н< 0 –повышение частоты.

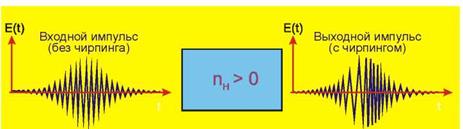
Рисунок 1.18 – Эффект чирпирования оптического импульса

ФСМ ‑ явление, которое ведет к симметричному спектральному уширению оптических импульсов. Уширение спектра из-за ФСМ возникает вследствие зависимости фазы импульса от времени, которая означает сдвиг мгновенной оптической частоты от основной частоты w₀ при перемещении вдоль импульса. Зависимость изменения частоты от времени можно рассматривать как частотную модуляцию импульса. Частотная модуляция наводится ФСМ и растет по величине с длиной распространения. Таким образом, генерация новых частотных компонент происходит непрерывно по мере распространения по световоду, вызывая уширение спектра по отношению к его начальной ширине при z = 0. Степень спектрального уширения зависит от формы импульса и от начальной частоты модуляции импульса.

Отметим важный практический момент, что эффект SPM приводит к появлению чирпинга примерно также, как и при распространении импульса в волокне с дисперсией (например, с SMF-28 на длине волны 1550 нм). Однако между этими явлениями имеются существенные отличия. Эффект SPM вызывает расширение спектра импульса (нелинейные искажения), но не меняет длительность импульса. Дисперсия же, наоборот, приводит к изменению длительности импульса, но не меняет ширину его спектра (линейные искажения). Характер распространения оптического импульса зависит от взаимодействия ФСМ и ДГС.

Как уже говорилось, в оптической связи термин ”дисперсия” связывается с уширением импульсов. Также вспомним, что в рабочем диапазоне длин волн:

a) коэффициент преломления n(λ) уменьшается с ростом длины волны λ;

b) фазовая скорость волны v_ф увеличивается с ростом λ.

c) минимальное значение группового показателя преломления N_гр(λ) – в точке нулевой дисперсии λ₀.

Как видно из рисунка 1.19 дисперсия изменяет знак на длине волны λ = λ₀ (для чистого кварца длина волны нулевой дисперсии λ₀ = 1,276 мкм). Это значение соответствует точке перегиба кривой n(λ).

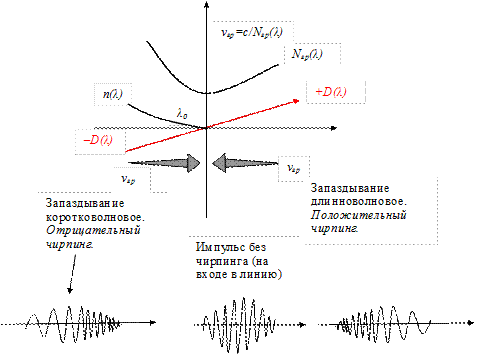
Рисунок 1.19 – Изменение знака дисперсии

Известно, что импульс характеризуется (во времени) не только длительностью и формой, но зависимостью частоты несущей от времени (чирпингом). Импульс на входе в линию промодулирован только по амплитуде, и частота его несущей не зависит от времени (чирпинга нет). Импульс без чирпинга, пройдя через волокно с положительной по знаку хроматической дисперсией, приобретает дополнительную частотную модуляцию (положительный чирпинг) и при этом уширяется. Уширяется импульс потому, что в волокне с дисперсией разные спектральные компоненты импульса движутся с разной скоростью. А положительный чирпинг импульс приобретает потому, что при положительной дисперсии длинноволновые компоненты запаздывают сильнее, чем коротковолновые, при этом происходит, так называемый, набег фазы. Если бы волокно обладало хроматической дисперсией с отрицательным знаком, то импульс бы всё равно уширился, но приобрёл бы при этом отрицательный чирпинг. Это приводит только к появлению зависящего от частоты фазового сдвига между амплитудами его спектральных составляющих. Сам же спектр при этом не меняется (рисунок 1.20). Поэтому про такой импульс говорят, что он уширен не по Фурье. Таким образом, в линейном приближении дисперсия приводит только к изменению ширины импульса, но не меняет ширину его спектра.

Рисунок 1.20 - Уширение импульса

Ранее было отмечено, что эффект фазовой самомодуляции приводит к уширению спектра импульса. При этом частота несущей на заднем фронте импульса оказывается больше частоты несущей на переднем фронте импульса (отрицательный чирпинг). Нелинейные эффекты из-за повышенной интенсивности волны порождают новые частотные компоненты, что приводит к уширению спектра импульса. И если при этом учесть эффект Керра, то в волокне с нулевой дисперсией импульс приобретает отрицательный чирпинг.

С увеличением мощности излучения в волокне с отрицательной дисперсией ширина импульса увеличивается вследствие того, что длина волны на хвосте импульса оказывается короче длины волны на фронте импульса. А так как в волокне с отрицательной дисперсией скорость распространения волн уменьшается с уменьшением длины волны, то хвост импульса начинает отставать от фронта, и ширина импульса увеличивается.

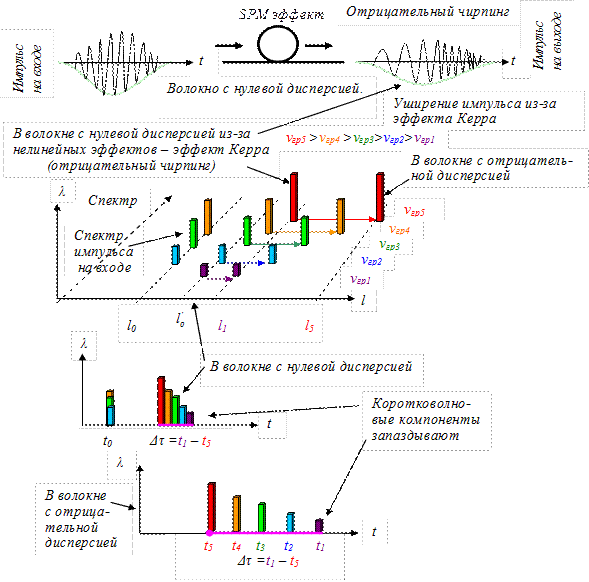
Рисунок 1.21 – Чирп-эффект в волокне с отрицательной дисперсией

В волокне с положительной дисперсией (рисунок 1.22) хвост импульса (с более короткими волнами) ускоряется, а фронт (с более длинными волнами) замедляется, что и приводит к сжатию импульса. Следует учесть, что сжатие импульса имеет место только при не слишком большой мощности, когда уширение импульса из-за эффекта Керра ещё мало. При большой мощности уширение импульса (из-за эффекта Керра) становится уже основным фактором, определяющим ширину импульса при его распространении в волокне с дисперсией. Такой импульс уширяется независимо от знака дисперсии волокна.

При некотором промежуточном значении мощности в волокне с положительной дисперсией эффект Керра уравновешивает влияние дисперсии. Другими словами, в то время, как дисперсия пытается сделать импульс более широким, эффект Керра обеспечивает его сжатие. Если оба эффекта сбалансированы, то форма импульса не изменяется. Такие импульсы называются солитонами. Солитон (soliton) – оптический импульс, не подвергающийся дисперсии при передаче на дальнее расстояние. Их применение в оптической связи весьма перспективно и в настоящее время сдерживается только стремительным развитием DWDM систем.

Рисунок 1.22 - Чирп-эффект в волокне с положительной дисперсией

Перекрестная фазовая модуляция (ХРМ – Cross-Phase Modulation) очень схожа с SPM, но рассматривается уже применительно к двум и более оптическим каналам, то есть применительно к ВОСП со спектральным мультиплексированием (CWDM/DWDM системам). Точно также, как и при SPM, возникает изменение рефракционного индекса n при увеличении интенсивности света. В WDM-системах с большим количеством каналов изменение линейной частотной модуляции импульса в одном канале зависит от вариации показателя преломления из-за интенсивности других каналов, усиливая SPM. Так как канальные уровни мощностей в CWDM/DWDM системах примерно одинаковы, то при ХРМ эффекте эффект увеличивает нелинейный фазовый сдвиг примерно в 2N раз, где N – число задействованных оптических каналов в ОВ. ХРМ приводит к таким же искажениям импульсов, как и SPM, только еще в большей степени. Характерно отметить, что эффект ХРМ в большей степени зависит от дисперсии ОВ по сравнению с SPM, что в свою очередь обуславливает необходимость увеличения запаса по дисперсии.

Для снижения влияния ХРМ необходимо выбирать оптические волокна с максимально возможной эффективной площадью сечения (данное замечание относится ко всем видам искажений) и, по возможности, снижать канальный уровень оптической мощности (см. рисунок 1.23).

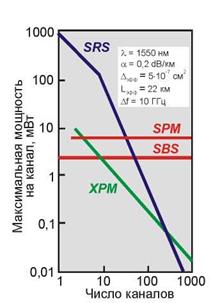
Рисунок 1.23 – Зависимость нелинейных эффектов от уровня оптической мощности

Важно также отметить, что ХРМ приводит также к появлению амплитудных искажений временного джиттера (рисунок 1.24). Эти искажения проявляются тем сильнее, чем выше скорость передачи и меньше интервал частот между каналами. Исследования в этом направлении стали интенсивно проводиться только в самое последнее время.

Рисунок 1.24 – Амплитудные искажения и временной джиттер оптических импульсов при XPM

Интермодуляция (IM – Inter Modulation) аналогична SPM и ХРМ, но рассматривается для нескольких каналов. Как и в выше рассмотренных случаях, величина рефракционного индекса изменяется пропорционально интенсивности оптической мощности. Так, например, если в ОВ присутствуют две независимые волны l₁ и l₂, то n будет изменяться синхронно их суммарной мощности, что вызовет появление комбинационных составляющих, то есть новых двух волн, близлежащих по частотному диапазону: 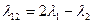и 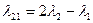. Такое явление подобно множеству способов формирования нелинейности при четырехволновом смешении (FWM).

Модуляционная нестабильность (MI –Modulation Instabliting) наблюдается только в ОВ с положительной дисперсией. Во временном представлении MI проявляется в виде пичков на импульсах (рисунок 1.25 а), а в спектральном – как уширение спектра импульса (рисунок 1.25 б).

Появление пичков на импульсах связано с эффектом самовоздействия волн. Этот эффект приводит к тому, что длина волны на заднем фронте импульса оказывается короче длины волны на переднем фронте. Волокно с положительной дисперсией ускоряет волну заднего фронта сильнее, чем более длинную волну переднего фронта. Когда задний фронт входит во взаимодействие с передним фронтом, возникает интерференция, которая и служит причиной образования пичков на передаваемых импульсах. После взаимодействие с передним фронтом, возникает интерференция, которая и служит причиной образования пичков на передаваемых импульсах. После детектирования оптического сигнала и последующей электрической фильтрации амплитуда пичков уменьшается так, что они не оказывают существенного влияния на работу систем протяженностью менее 1000 км.

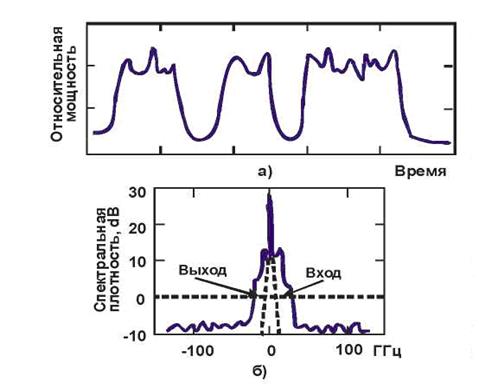
Рисунок 1.25 – Влияние на оптический импульс модуляционной нестабильности

Эффект четырехволонового смешения ЧВС/FWM проявляется только в многоволновых системах. В системах WDM, использующих световые волны с близкими частотами, зависимость показателя преломления от интенсивности не только вызывает смещение фазы внутри канала, но и создаёт сигналы на новых частотах. Для этого достаточно, чтобы в нелинейном взаимодействии участвовало не менее двух световых волн с близкими частотами f₁ и f₂ (то есть в одном окне прозрачности). В этом случае по полной аналогии с электрическими цепями, между ними будет наблюдаться нелинейное взаимодействие в силу нелинейности передаточной функции, будь она активной (то есть с усилением) или пассивной (с ослаблением). Тогда согласно рисунку 1.26 появившиеся при нелинейном взаимодействии комбинационные частоты (2f₁ – f₂ и 2f₂ – f₁) будут близки к исходным и располагаются в рассматриваемом диапазоне частот (длин волн).

Если же в нелинейном взаимодействии участвуют три световые волны с близкими частотами (f_i, f_j, f_k), то некоторые из вновь созданных комбинационных частот f_i ± f_j ± f_k также будут близки к исходным частотам и попадут в спектральные каналы CWDM/DWDM системы и вызовут перекрёстные помехи. Наибольшее беспокойство вызывает сигнал, соответствующий

f_ijk = f_i + f_j – f_k, (1.44)

где f_ijk – частота появившейся новой четвёртой волны, которая близка к частотам породивших её волн.

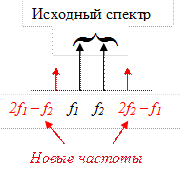
Рисунок 1.26 - Нелинейное взаимодействие при двух световых волнах

В качестве примера рассмотрим простейшую систему с тремя длинами волн (l₁, l₂, l₃), которая подвержена FWM искажениям. В такой системе возникнут девять длин волн, обязанных исходным сигналам (см. рисунок 1.27). На самом деле число интермодуляционных продуктов много больше, но они располагаются достаточно далеко от исходных входных длин волн. Предположим, что входные волны составляют: l₁=1551,72 нм; l₂=1552,52 нм; l₃=1553,32 нм. Комбинационные продукты третьего порядка составят значения: l₁+l₂-l₃=1550,92 нм; l₁-l₂+l₃=1552,52 нм; l₂+l₃+l₁=1554,12 нм; l₁-l₂+l₃=1552,52 нм; l₂+l₃-l₁=1554,12 нм; 2l₁-l₃=1550,12 нм; 2l₃-l₁=1554,92 нм; 2l₂-l₁=1553,32 нм; 2l₃-l₂=1554,12 нм.

Рисунок 1.27 – Распределение продуктов ЧВС

Можно заметить, что три составляющие интермодуляционных искажений по длине волны совпадают с исходными сигналами. Оставшиеся шесть составляющих немного частотно смещены (см. рисунок 1.27) и принципиально могут быть отфильтрованы. Ситуация много усложняется с ростом числа исходных сигналов N, так как число интермодуляционных составляющих резко увеличивается по формуле:

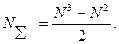( 1.45)

На рисунке 1.28 показана зависимость общего числа интермодуляционных составляющих от числа исходных сигналов. Так, для 4, 8 и 16-ти исходных сигналов число комбинационных составляющих составит соответственно 24, 224 и 1920.

Никакая фильтрация уже не способна устранить близлежащие или совпадающие по частоте продукты интермодуляции. В силу этого системы с грубым спектральным мультиплексированием СWDM являются значительно более помехозащищенными в сравнении с системами плотного волнового мультиплексирования DWDM, что вполне логично. Также при равном числе транслируемых каналов (например, до 8), системы DWDM значительно более помехозащищены в силу большей избирательности и большей узкополосности самих оптических передатчиков.

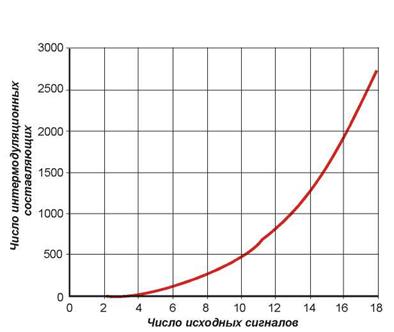
Рисунок 1.28 – Зависимость интермодуляционных составляющих от числа исходных сигналов

Таким образом, единственным способом защиты от FWM при большом числе транслируемых каналов является устранение причин ее возникновения. На эффективность FWM (то есть на величину возникающих интермодуляционных составляющих) влияют два основных фактора: межканальный интервал расстановки оптических несущих (типовые значения 0,8 нм или 100 ГГц; 0,4 нм или 50 ГГц и 0,2 нм или 25 ГГц) и волоконная дисперсия (D). С увеличением межканального интервала эффективность FWM понижается при любой дисперсии ОВ (см. рисунок 1.29).

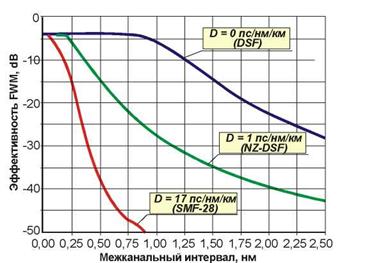
Рисунок 1.29 – Зависимость эффективности ЧВС/FWM от межканального интервала

Возникающие при FWM новые волны могут приводить к деградации распространяемого оптического сигнала, интерферируя с ними, или перекачивать мощность из полезного волнового канала. Установлено, что явление смешения четырёх волн зависит от фазового отношения между взаимодействующими сигналами. Как это ни парадоксально, но понизить эффективность FWM можно именно с помощью хроматической дисперсии, т.е. при использовании стандартного одномодового ОВ без смещения (SMF-28). Дело в том, что на выходе лазеров формируется когерентное световое излучение, в котором сигналы находятся в привязанной фазе по отношению друг к другу. Если все взаимодействующие сигналы распространяются по волокну с одной и той же групповой скоростью, что происходит при отсутствии дисперсии, то между собой, они образуют новую волну. Этому эффекту в значительной степени противодействует дисперсия, обеспечивающая условия, при которых согласованность фаз сигналов не может сохраниться после прохождения ими больших расстояний. При наличии дисперсии различные сигналы распространяются с различными групповыми скоростями, что приводит к снижению эффекта смешения (рисунок 1.30).

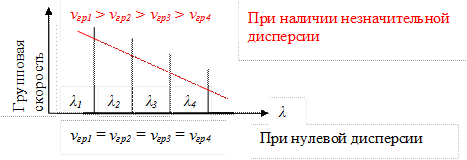
Рисунок 1.30 – Зависимость групповой скорости от дисперсии

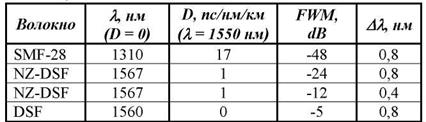
В системах с дисперсией отличие скоростей больше, когда каналы расположены дальше друг от друга. Для примера в таблице 1.2 приведены типовые значения эффективности FWM при шаге расстановки в 100 ГГц (0,8 нм) для ВОК протяженностью в 100 км при канальной мощности возбуждения +10 dBm. Как видно из таблицы, при использовании стандартного одномодового волокна (SMF-28), эффективность FWM является низкой. Однако следует иметь в виду, что указанное значение в -47 dB заявлено только для трех каналов. В реальных системах их может быть больше.

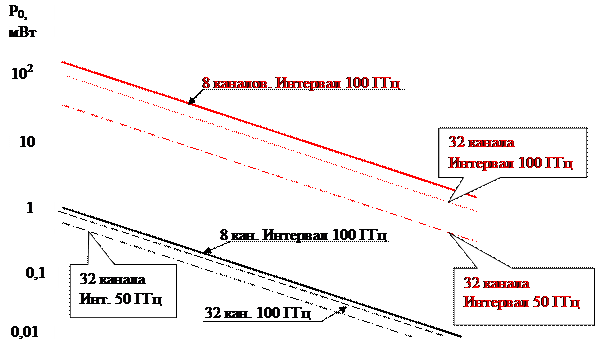
Известно, что мощность четырёхволнового смешения возрастает с увеличением длины линии, а это, в свою очередь, устанавливает ограничения на передаваемую мощность для каждого канала в зависимости от её длины. Данное ограничение отражено на рисунке 1.31, как для стандартного одномодового волокна (SMF), так и для волокна со смещённой дисперсией (DSF) при трёх случаях расположения каналов.

Таблица 1.2

1 10 100 1000 L, км

Рисунок 1.31 - Ограничение мощности в канале из-за FWM

Как следует из рисунка 1.31, максимальное значение передаваемой мощности в случае использования волокна со смещённой дисперсией значительно меньше, чем для стандартного волокна. Это связано с тем, что вследствие низкого показателя дисперсии эффективность смешения четырёх волн в волокне со смещённой дисперсией значительно выше. Сравнивая ограничения для 8-канальной и 32-канальных систем с одинаковыми интервалами 100 ГГц, видим, что уровень ограничения мощности уменьшается с увеличением числа каналов, так как количество элементов смешения четырёх волн увеличивается с их числом. В случае использования волокна со смещённой дисперсией это уменьшение неощутимо, несмотря на то, что в 32-канальной системе существует много спектральных составляющих. Это объясняется тем, что те же самые 8 каналов вблизи нулевой дисперсии содержат почти всю мощность смешения четырёх волн, как и случае 8-канальной системы, а вклад мощности смешения четырёх волн от других каналов невелик, так как на этих длинах волн дисперсия намного больше. Наконец, ограничение мощности существенно уменьшается при уменьшении интервалов между каналами, что следует из сравнения кривых для двух 32-канальных систем с интервалами 100 и 50 ГГц.

Таким образом, для снижения эффекта смешения четырёх волн необходимо уменьшать передаваемую мощность и увеличивать интервал между каналами. Однако это приводит к различию групповых скоростей между каналами и, как следствие, к увеличению полосы пропускания всей системы.

Волокно со смещённой дисперсией (DSF) имеет в третьем окне прозрачности наименьшие значения затухания и дисперсии. Причём, нулевая дисперсия находится в середине передаваемой полосы каналов с коэффициентом наклона кривой дисперсии S_o=0,055 пс/(нм²·км). Однако, это выгодно только для случая передачи одной длины волны – одноканальной передачи. Исследования показали, что если длина волны нулевой дисперсии попадает в зону мультиплексного сигнала, начинают проявляться нежелательные интерференционные эффекты, приводящие к более быстрой деградации сигнала. Поэтому смешение четырёх волн представляет серьёзную проблему в системах WDM, использующих волокно со смещённой дисперсией (DSF), но обычно не вызывает проблем в системах со стандартным волокном.

В случае использования волокна со смещённой дисперсией максимальная величина передаваемой мощности значительно меньше, чем для стандартного волокна. Это связано с тем, что вследствие низкого показателя дисперсии эффективность смешения четырёх волн в волокне со смещённой дисперсией значительно выше. Поэтому, чтобы избежать нелинейных эффектов при использовании DSF в системах WDM, следует вводить в волокно сигнал меньшей мощности, увеличивать расстояние между каналами и избегать передачи парных каналов (симметричных относительно λ_о).

Поскольку смешение четырёх волн представляет серьёзную проблему в системах WDM, использующих волокно со смещённой дисперсией, стало ясно, что необходимо разработать новый тип волокна, в котором λ₀ располагалась бы вдали, то есть, по одну сторону (левее или правее) от всех возможных каналов. В 90-х годах было создано волокно со смещенной ненулевой дисперсией. Так как длина волны нулевой дисперсии вынесена за пределы окна 1550 нм, то волна не захватывает полосу пропускания эрбия. Это уменьшает нелинейные эффекты и улучшает характеристики волокна при передаче DWDM сигнала.

Мощность четвертой волны Р₄ зависит от множества факторов и записывается в виде:

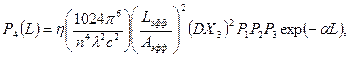(1.46)

где h - эффективность ЧВС;

L – геометрическая длина ОВ;

l - длина волны;

С=3*10^-5 км/с – скорость света;

L_эфф – эффективная длина ОВ;

DX₃ – деградирующий фактор, зависящий от межканального расстояния и хроматической дисперсии используемого волокна;

Р₁, Р₂, Р₃ – вводимые оптические мощности на различных длинах волн;

a - погонные потери ОВ.

Эффективная длина оптического волокна L_эфф зависит от его геометрической длины L и погонных потерь a:

(1.47)

В выражении (1.46) величину погонных потерь a необходимо подставлять в неперах на километр. Формула пересчета имеет вид:

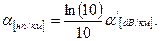(1.48)

Более удобно пользоваться непосредственно в традиционных справочных значениях, то есть в дБ/км. Для этого выражение (1.46) можно переписать в виде, удобном для практического использования:

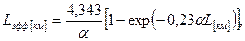(1.49)

График зависимости L_эффот геометрических размеров ОВ для разных значений погонных потерь a’ представлен на рисунке 1.32. Для длинных линий (свыше 40 км) эффективная длина ОВ при типовом значении погонных потерь a=0,22 дБ/км составляет порядка 20 км.

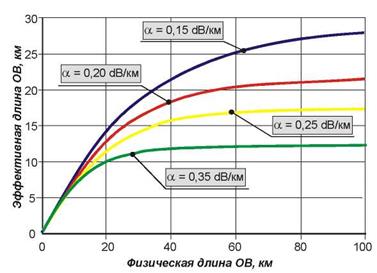
Рисунок 1.32 – Зависимость эффективной длины от физической длины ОВ

В свою очередь, эффективность четырехволнового смешения h может быть выражена зависимостью:

(1.50)

где к – коэффициент, зависящий от межчастотного интервала расстановки каналов (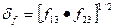) и состояния поляризационной согласованности.

На основе рассмотренных выше выражений можно получить приближенную формулу по расчету эффективности FWM_pдля волокна SMF-28, наиболее часто используемого на практике для России, с учетом частотного шага расстановки Nканалов d_f, может быть записано в виде:

(1.51)

Так, для 8-ми канальной WDM с шагом частотной расстановки в d_f = 200 ГГц (192,4– 193,8 ТГц) FWM_pсоставит примерно -46,7 дБ, а для 16-ти канальной расстановки с частотным шагом в 100 ГГц FWM_pсоставит -37,7 дБ. Электрический эквивалент FWM_pравен удвоенному значению оптической эффективности и для последнего случая будет равен -75,4 дБ.