 |
Производная в параллельном и последовательном соединениях цепей
|
|
|
|
Содержание
1. Производная в кинематике
2. Производная в электрическом сопротивлении
. Производная в термодинамике
. Производная в электродинамике
. Производная в геометрической оптике
. Производная в механических колебаниях
. Производная в статике
. Производная в параллельном и последовательном соединениях цепей
. Производная в законе сохранения энергии
Список используемой литературы
Производная в кинематике
Кинематика: если изменение координаты задано уравнением вида x = x(t), то производная первого порядка от координаты по времени есть скорость, то есть (t) = x'(t), а производная второго порядка от координаты по времени, или производная первого порядка от скорости по времени, есть ускорение, значит a(t) = x"(t) = ' (t).
Дано: H-? S-?
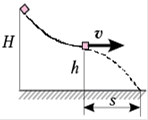
Решение:
Закон сохранения механической энергии:
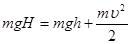
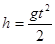- по вертикали;
- по горизонтали, т. к. 
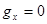
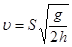
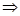
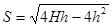
Затем исследуем зависимость, находим производную по переменной h и приравниваем её к нулю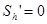 
т.е. расстояние S будет наибольшим при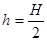 
когда производная обращается в нуль: 4H - 8h = 0.
Подставляя полученное выражение для высоты трамплина h = H/2 в формулу для S, получаем S = H.
Ответ: S=H
Производная в электрическом сопротивлении
Для возникновения постоянного тока в металлических проводниках на свободные электроны должно действовать электрическое поле, способное обеспечить на концах проводника постоянную разность потенциалов. Каждый источник тока характеризуется электродвижущей силой 
.
Дано: Решение:
R=0,9 Ом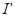 
k - (nE(R - nr / k)) / (kR + nr / k) 2=0
n=36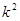 
=nr / R=2B 
= 
= 
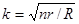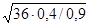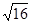=4=0,4 Ом m=n/k
|
|
|
m=36/4=9, m, Imax -? Imax = nE / (kR+mr) =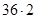 
/ (
+ 
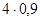) = 10A
Ответ: 4; 9; 10А
Производная в термодинамике
Термодинамические потенциалы - это функции параметров состояния макроскопической системы для описания термодинамического равновесия. Каждому термодинамическому потенциалу соответствует набор параметров состояния, называемых естественными переменными.
Термодинамика: использование производной позволяет решать задачи на нахождение экстремальных значений параметров в циклах идеального газа.
Дано: Решение:
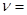1моль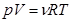 
- уравнение Клайперона - Менделеева
; 
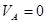
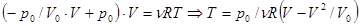
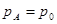
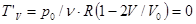
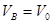
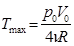
Ответ: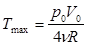 
Производная в электродинамике
Электромагнитная индукция: производная от магнитного потока по времени, взятая с противоположным знаком (по правилу Ленца), позволяет определить мгновенное значение ЭДС, индуцируемой в замкнутом проводящем контуре: i = -Ф' (t);
Дано: Решение:
S=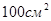 
= 
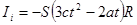
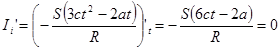
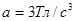
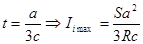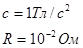
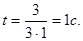
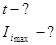
Ответ: 1с, 3А.
Производная в геометрической оптике
Геометрическая оптика: используя принцип Ферма, можно вывести закон преломления света. Принцип Ферма в геометрической оптике - предписывает лучу света двигаться из начальной точки в конечную точку. Свет выбирает один путь из множества близлежащих, требующих почти одинакового времени для прохождения; другими словами, любое малое изменение этого пути не приводит в первом порядке к изменению времени прохождения.
Дано: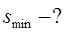 
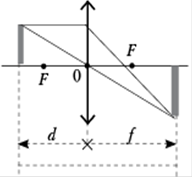
Решение:
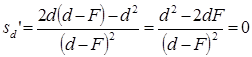
Из равенства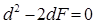 
следует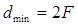 
Ответ: 4F.
Производная в механических колебаниях
Механические колебания: энергетический подход (метод производной) позволяет вывести дифференциальные уравнения второго порядка, описывающие процессы в математическом и пружинном маятниках, затем получить формулы для периодов колебаний, а также рассчитать период колебаний сложных колебательных систем;
|
|
|
Дано:
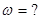
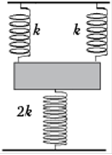
Решение:
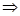
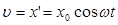
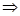изменение кинетической энергии колеблющегося тела происходит с частотой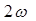 
Ответ: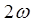 
Производная в статике
Дано:
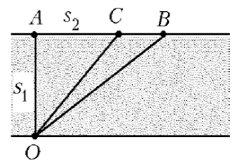
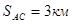
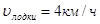
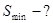
Решение:
Пусть АС = x, тогда СВ = (5 - x)
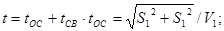
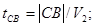
f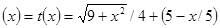 
f 
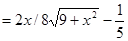
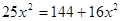
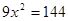
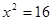
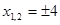
Ответ: чтобы затратить на путь из O в B наименьшее время, надо высадиться в 4 км от A.
Производная в параллельном и последовательном соединениях цепей
Отдельные участки цепи (резисторы) можно соединять последовательно и параллельно. При последовательном соединении резисторы включаются один за другим, поэтому сила тока на всех участках цепи одинакова, а общее или эквивалентное сопротивление цепи равно:
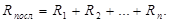
производная оптика термодинамика
Дано: Решение:
9 раз >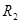 
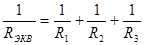
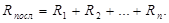
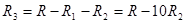; тогда
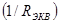
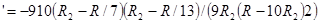
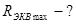
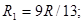
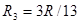
Ответ: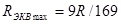 
|
|
|
