 |
The development of the scheme of transformer’s structure
|
|
|
|
The transformer is based on two principles: firstly, that an electric current can produce a magnetic field (electromagnetism) and secondly that a changing magnetic field within a coil of wire induces a voltage across the ends of the coil (electromagnetic induction). Changing the current in the primary coil changes the magnetic flux that is developed. The changing magnetic flux induces a voltage in the secondary coil.

Figure 1.4 – An ideal transformer
An ideal transformer is shown in the adjacent figure. Current passing through the primary coil creates a magnetic field. The primary and secondary coils are wrapped around a core of very high magnetic permeability, such as iron, so that most of the magnetic flux passes through both the primary and secondary coils.
Models of an ideal transformer typically assume a core of negligible reluctance with two windings of zero resistance. When a voltage is applied to the primary winding, a small current flows, driving flux around the magnetic circuit of the core. The current required to create the flux is termed the magnetizing current; since the ideal core has been assumed to have near-zero reluctance, the magnetizing current is negligible, although still required to create the magnetic field.
The changing magnetic field induces an electromotive force (EMF) across each winding. Since the ideal windings have no impedance, they have no associated voltage drop, and so the voltages VP and VS measured at the terminals of the transformer, are equal to the corresponding EMFs. The primary EMF, acting as it does in opposition to the primary voltage, is sometimes termed the "back EMF". This is due to Lenz's law which states that the induction of EMF would always be such that it will oppose development of any such change in magnetic field.
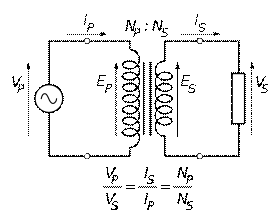
Figure 1.5 – The ideal transformer as a circuit element
If the secondary coil is attached to a load that allows current to flow, electrical power is transmitted from the primary circuit to the secondary circuit. Ideally, the transformer is perfectly efficient; all the incoming energy is transformed from the primary circuit to the magnetic field and into the secondary circuit. If this condition is met, the incoming electric power must equal the outgoing power.
An ideal transformer would have no energy losses, and would be 100% efficient. In practical transformers energy is dissipated in the windings, core, and surrounding structures. Larger transformers are generally more efficient, and those rated for electricity distribution usually perform better than 98%.Experimental transformers using superconducting windings achieve efficiencies of 99.85%.While the increase in efficiency is small, when applied to large heavily loaded transformers the annual savings in energy losses are significant.
A small transformer, such as a plug-in "wall wart" power adapter commonly used for low-power consumer electronics devices, may be as low as 20% efficient, with considerable energy loss even when not supplying any power to the device. Though individual losses may be only a few watts, it has been estimated that the cumulative loss from such transformers in the United States alone exceeded 32 billion kilowatt-hours (kWh) in 2002.
|
|
|
The losses vary with load current, and may be expressed as "no-load" or "full-load" loss. Winding resistance dominates load losses, whereas hysteresis and eddy currents losses contribute to over 99% of the no-load loss. The no-load loss can be significant, meaning that even an idle transformer constitutes a drain on an electrical supply, which encourages development of low-loss transformers (also see energy efficient transformer).
Transformer losses are divided into losses in the windings, termed copper loss, and those in the magnetic circuit, termed iron loss. Losses in the transformer arise from:
Winding resistance
Current flowing through the windings causes resistive heating of the conductors. At higher frequencies, skin effect and proximity effect create additional winding resistance and losses.
Hysteresis losses
Each time the magnetic field is reversed, a small amount of energy is lost due to hysteresis within the core. For a given core material, the loss is proportional to the frequency, and is a function of the peak flux density to which it is subjected.
Eddy currents
Ferromagnetic materials are also good conductors, and a solid core made from such a material also constitutes a single short-circuited turn throughout its entire length. Eddy currents therefore circulate within the core in a plane normal to the flux, and are responsible for resistive heating of the core material. The eddy current loss is a complex function of the square of supply frequency and inverse square of the material thickness.
Magnetostriction
Magnetic flux in a ferromagnetic material, such as the core, causes it to physically expand and contract slightly with each cycle of the magnetic field, an effect known as magnetostriction. This produces the buzzing sound commonly associated with transformers, and in turn causes losses due to frictional heating in susceptible cores.
Mechanical losses
In addition to magnetostriction, the alternating magnetic field causes fluctuating electromagnetic forces between the primary and secondary windings. These incite vibrations within nearby metalwork, adding to the buzzing noise, and consuming a small amount of power.
Stray losses
Leakage inductance is by itself largely lossless, since energy supplied to its magnetic fields is returned to the supply with the next half-cycle. However, any leakage flux that intercepts nearby conductive materials such as the transformer's support structure will give rise to eddy currents and be converted to heat. There are also radiative losses due to the oscillating magnetic field, but these are usually small.
In the case when it is used the transformer that is feeding from the single phase network (U c = 220 V) with the load 1…100 VA and the voltage U 0 < 1000 V, then it is given preference to the shell type of core.
When the power is placed in the range from several tens to the several hundreds VA, it is better to use bar magnetic cores. The core-type transformers have two inductance coils that are divided into bars. The advantages of such transformer are the following items:
|
|
|
· low leakage inductance because only half quantity of the coil’s number is placed on the each inductance coil and it has smaller width of winding;
· smaller consumption coils wire is used than shell-type transformer uses because the average length of coil is smaller;
· the responsivity is much lower than in shell-type transformer, because the emf of noise in both inductive coils have different phase that’s why they are deleted by each other.






Figure 2.4 – The scheme of single-phase magnetic core:
a) bar ribbon core ПЛ, ПЛМ (S = 2); b) shell-type transformer ШЛ, ШЛМ (S = 1)
In the case when it is used the transformer that is feeding from the three phase network (U c = 380/220 V) it is used three phase transformer. Their inductive coils are placed on each bar. To realize such transformer it is used the magnetic cores of laminated or ribbon type as it is shown on the figure 2.5.
For three phase transformer it developed the special set of magnetic core of ribbon type for the power that is not less than 1 kW.

Figure 2.5 – The scheme of three-phase magnetic core (S=3):
a) laminated TП; b) ribbon TЛ
b)
Table 2.1 – The suggested parameters of magnetic core
| Magnetic core | Frequency, Hz | Parameter of magnetic core | Total power in the secondary winding P2, VA | |||
| type | material | 150…300 | 300…1000 | 1000…2500 | ||
| ШЛ ШЛМ shell-type | Δ = 0,35 | BS, T | 1,65 | 1,65 | - | |
| j, A/mm2 | 2,4-2,3 | 2,3-1,8 | - | |||
| k 0 | U0 = 100V | 0,32-0,34 | 0,34-0,38 | - | ||
| U0 = 102…103 | 0,27-0,3 | 0,3-0,33 | - | |||
| ПЛ ПЛМ ТЛ ribbon- type | Δ = 0,35 | BS, T | 1,6 | 1,6 | 1,6 | |
| j, A/mm2 | 3,0-2,4 | 2,4-0,35 | 1,7-1,4 | |||
| k 0 | U0 = 100V | 0,29-0,3 | 0,3-0,35 | 0,35 | ||
| U0 = 102…103 | 0,25-0,3 | 0,3 | 0,3 |
The choice of magnetic core type is finished if the chosen type can contain the necessary windings with aperture occupation ratio by kM  0,25…0,35.
0,25…0,35.
For the chosen magnetic core of transformer from the table 2.4 it is defined the values of flux density Bm, current density in the windings j, aperture occupation ratio k0 and material of magnetic core. When the material of magnetic core and its construction are defined from the table 2.5, it is used the value kc that is the space factor of cross-section Sc by steel to define the width of ribbon.
The developed transformer contains S number of leg on which the windings are placed. The windings placement is defined by the coefficient k0. When S=2 the windings are placed on two legs of transformer and the coils are connected sequentially. In this case for bridge scheme will be K0 = 0,5 and for other ones K0 = 1.
Table 2.5 – Construction parameters of magnetic core
| Construction of magnetic core | Isolation of bar or ribbon | Aperture occupation ratio k c when the width of steel is Δ = 0,35 |
| Plate | Dope Phosphate film | 0,9 0,94 |
| Ribbon | Dope, enamel | 0,93 |
When the calculation is done all results have to be shown in the table 2.6.
Table 2.6 – Parameters of transformer
| Type and material of the core | B m, T | j, A/mm2 | k 0 | k cs | S | K 0 |
| Values |
|
|
|


