 |
Логический риск сбоя
|
|
|
|
Статические риски сбоя
На рис. 6 показана работа элементов И и ИЛИ при подаче на их входы двух последовательных во времени наборов Х1 = x 1 x 0 = 01 и Х2 = x 1 x 0 = 10. Значение сигнала у1 для элемента И на этих наборах должно оставаться постоянным и равным 0, а у2 – равным 1. Это выполняется для случаев разброса во времени моментов переключения переменных x 1 и x 0, показанных на рис. 6, а и г.
Рис. 6. Разброс во времени моментов переключения
Если же этот разброс соответствует рис. 6, б и в, то видно, что на выходе схемы И появится логический сигнал 1 длительностью Δτ1, а на выходе схемы ИЛИ - сигнал 0 длительностью Δτ2. Эти ложные сигналы и являются рисками сбоя, причем видно, что они могут быть, а могут и отсутствовать. Все дальнейшие примеры будут иллюстрироваться временными диаграммами для наихудшего случая, когда риск сбоя обязательно имеет место.
Риск сбоя называется статическим, если у (X1) = y (Х2), где y - булева функция. Риск сбоя называется статическим в нуле S0, если у (X1) = y (Х2) = 0. Риск сбоя называется статическим в единице S1, если у (X1) = y (Х2) = 1. Итак, на рис. 6, б имеет место статический риск сбоя в нуле S0, а на рис. 6, в - статический риск сбоя в единице S1.
Существенно, что полученные помехи S0 и S1 (иногда их называют “иголками”, “мерцаниями”, “глитчами” (англ. glitch)) - это не пренебрежимо короткий всплеск напряжения малой амплитуды. При достаточно большой разности Δτ помеха будет иметь длительность, во много раз превышающую время переключения элемента, и амплитуду, равную номинальному сигналу. Это уже полноценный сигнал, на который могут реагировать последующие элементы (входы синхронизации, установки в 0 или 1, загрузки данных и т. п.). Такие помехи - страшная вещь для цифровых схем, тем более, что их практически невозможно увидеть на осциллографе, и разработчик просто не будет знать об их существовании. Они могут сужаться до полного исчезновения, но могут и расширяться, проходя через логические цепи.
|
|
|
Динамические риски сбоя
На рис. 7, а приведена схема, реализующая функцию у = x 2 x 1 + x 0. Пусть входной набор Х1 = x 2 x 1 x 0 = 010 изменяется на входной набор Х2 = x 2 x 1 x 0 = 101. На рис. 7, б приведены временные диаграммы, соответствующие наихудшему случаю разброса моментов переключения переменных x 2, x 1 и x 0. Поскольку у (X1) = 0, а y (Х2) = 1, из рис. 7, б видно, что на выходе схемы имеет место многократное переключение вместо идеального алгоритмического перехода 01. Пусть входной набор Х1 = x 2 x 1 x 0 = 011 изменяется на входной набор Х2 = x 2 x 1 x 0 = 100. Из рис. 7, в видно, что вместо идеального алгоритмического перехода 10 на выходе имеет место многократное переключение.
Рис. 7. Наихудший случай разброса во времени моментов переключения
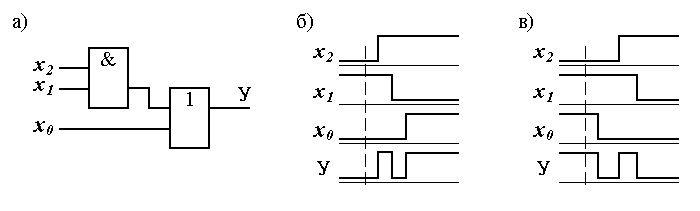
Риск сбоя называется динамическим, если у (X1) ≠ y (Х2), где y - булева функция. Риск сбоя называется динамическим D+ при переходе на выходе 01, если у (X1) = 0, а y (Х2) = 1. Риск сбоя называется динамическим D–, если у (X1) = 1, а y (Х2) = 0. Итак, на рис. 7, б имеет место динамический риск сбоя D+, а на рис. 7, в - D–. Из временных диаграмм работы схемы видно, что динамический риск сбоя является
следствием статического риска сбоя. Наличие динамических рисков сбоя в цифровой схеме также может привести к нарушению закона ее функционирования.
Логический риск сбоя
Рассмотрим переход от Х1 = x 2 x 1 x 0 = 110 к Х2 = x 2 x 1 x 0 = 010 для функции у, представленной картой Карно (рис. 8, а). Для нее можно записать 
. На рис. 8, б приведена соответствующая схема.
Рис. 8. Логический риск сбоя
Обратите внимание, что в данном случае осуществляется переход между соседними наборами, причем x 1 = 1 и x 0 = 0 являются константными сигналами, следовательно, для функции можно записать в данном случае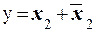 
. Ясно, что здесь у (X1) = y (Х2) = 1, однако мы видели (см. рис. 6, в), что на элементе ИЛИ возможен статический риск сбоя в единице. Это отражено также на рис. 8, в.
|
|
|
Попытаемся устранить этот риск сбоя, видоизменив аппаратную реализацию данной функции. Введем в карте Карно дополнительный контур, показанный штриховой линией, тогда уравнение для функции будет иметь вид 
(рис. 9, а). Так как при переходе от набора Х1 к Х2 простая импликанта 
все время равна 1, то риск сбоя, выявленный выше, не будет проявляться на выходе схемы. Эта ситуация отражена на временной диаграмме, представленной на рис. 9, б.
 |
Рис. 9. Статический риск сбоя
Статический риск сбоя, проявляющийся при соседней смене наборов, называется логическим, так как может быть устранен изменением логической структуры, реализующей булеву функцию.
|
|
|
