Число внутренних состояний ОА можно определить как

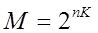
(4.1)

 

Так, при n =32, k =16 имеем M=2⁵¹². Очевидно, что при таком числе состояний канонический метод синтеза применить нельзя. Поэтому ОА синтезируются с использованием некоторого набора элементов, называемого структурным базисом. Наиболее часто для этих целей используется следующий набор элементов:

1. Регистры – для приёма, хранения и выдачи информации.

2. Комбинационные схемы – для вычисления новых значений слов информации.

3. Шины – для передачи информации между отдельными частями ОА.

Все эти элементы присутствуют в схеме на рис. 4.1. Отметим, что микрооперации y _nÎY формируются управляющим автоматом (УА) и логические условия x _lÎX является входными сигналами УА. Остановимся более подробно на организации шин.

Шина представляет собой совокупность проводников, предназначенных для передачи двоичной информации. Каждый проводник передаёт один бит информации, поэтому для передачи K бит информации шина должна включать K проводников. Условимся обозначать шину именем слова информации, которое по ней передаётся.

Простейшим видом является асинхронная шина, выполняющая микрооперацию передачи информации B=A. Условное обозначение шины приведено на рис. 4.2,а

 

 

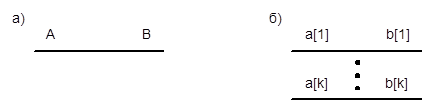
Рис. 4.2. Условное обозначение (а) и организация (б) асинхронной шины

 

Каждый провод этой шины организован идентично и k -й проводник (Рис. 4.2,б) выполняет операцию b [ k ]= a [ k ].

Управляемая шина выполняет операцию передачи информации только при наличии специального управляющего сигнала. Управляемая шина выполняет операцию

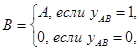
где у_AB - управляющий сигнал, инициирующий передачу информации. Таким образом, можно написать, что B= у_AB ×A, то есть b [ k ]= у_AB × a [ k ], k =1,…K. На рис. 4.3 приведено условное обозначение управляемой шины и схемы её k-го разряда.

 

 

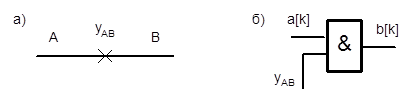
Рис. 4.3. Условное обозначение (а) и организация (б) управляемой шины

 

Для передачи информации от нескольких источников информации одному приёмнику используется сборка шин. Например, если информация из источника A_i передаётся к приёмнику B по сигналу y_i (i=1,…,I), то сборка выполняет функцию

 

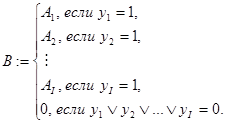
Следовательно, каждый разряд сборки выполняет функцию

На рис. 4.3 приведено условное обозначение и схема k-го разряда сборки шин

 

 

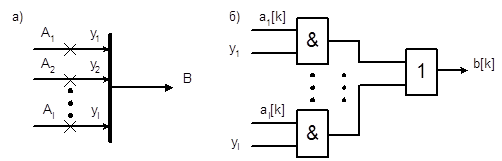
Рис. 4.3. Условное обозначение (а) и организация (б) сборки

 

Очевидно, функции сборки шин аналогичны функциям мультиплексора, рассмотренного в главе 2. Пусть I=3, закодируем наборы, < y₁y₂y₃ > двухразрядными кодами z₁z₂ следующим образом: 100®01, 010®11, 001®11, 000®00. В этом случае каждый элемент сборки реализуется следующим образом (Рис. 4.4,а)

 

 

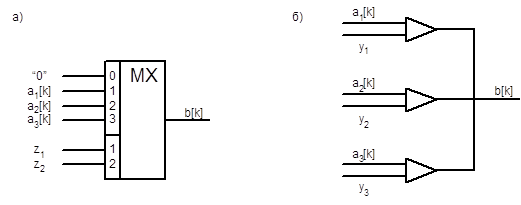
Рис. 4.4. Реализация сборки шин на мультиплексорах(а) и тристабильных элементах (б)

 

Наиболее часто для организации сборки используют элементы с трёмя состояниями. Одно из состояний соответствует логическому нулю, второе - единице, третье - высокоимпедансное состояние, в котором элемент отключён от шины. Для перевода схемы в третье состояние используется специальный сигнал, в нашем случае это сигнал передачи информации (Рис. 4.4,б). Если y_i =1, то слово A_i передаётся на выход B (i=1,2,3). Если y_i =0, то элемент передачи информации переводится в третье состояние и передачи не происходит. Условимся в дальнейшем именовать сборки шин мультиплексорами.

Так как в OA имеется обратная связь между комбинационной схемой и памятью, то регистры памяти должны состоять из двухтактных триггеров. В противном случае - как и в любом структурном автомате - возможны сбои в работе OA.

Формальные методы синтеза операционных автоматов, рассматриваемые в данной книге, разработаны С.А.Майоровым и Г.И.Новиковым [10]. Основой для синтеза схем OA являются функциональные микропрограммы, которые состоят из логических условий и типовых микроопераций.

 

 

4.2. Типовые микрооперации и функциональные микропрограммы

 

В процессе разработки средств цифровой вычислительной техники проектировщики пришли к определённому набору элементов, который используется при проектировании операционных автоматов. Каждый из таких элементов выполняет определённую элементарную обработку информации. Сигналы, инициирующие обработку информации стандартными операционными элементами, назовём типовыми микрооперациями. Типовые микрооперации делятся на классы:

1. Микрооперация установки.

В результате её выполнения слову информации (регистру) присваивается значение константы. Например, A:=01.

2. Микрооперация передачи.

Микрооперация инициирует передачу информации между регистрами (A:=B), в процессе которой некоторые разряды источника могут меняться.

3. Микрооперация инвертирования.

После выполнения операции значение слова изменяется на инверсное (A:=ùA). Микрооперация выполняется при помощи многоразрядного инвертора, включённого в цепь обратной связи регистра A (Рис. 4.5). Если y₁ =1, то выполняется поразрядное

 

 

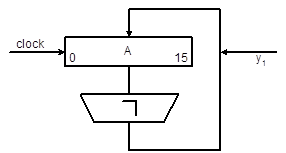
Рис. 4.5. Выполнение микрооперации инвертирования

 

инвертирования слова A и новое значение слова заносится в регистр по сигналу Clock. Знак „:=” означает, что в операции участвует регистр и слева в выражении находится содержимое регистра в момент времени t, а справа - t +1 (t =0,1,…). Если A^t=0101, то в результате выполнения микрооперации инвертирования A^t+1=1010 будет записано в регистр A.

4. Микрооперация сдвига.

Эти микрооперации предназначены для изменения положений разряда слова по отношению к первоначальному путём перемещения каждого разряда на n позиций влево или вправо.

Сдвиг на n разрядов вправо (A:=R_n(A)) приводит к потере n младших разрядов слова и заполнению старших n разрядов нулями. Например, R₂(110110)=001101, R₃(A)=000110.

Сдвиг на n разрядов влево (A:=L_n(A)) приводит к потере n старших разрядов слова и заполнению младших n разрядов нулями. Например, L₁(110110)=101100, L₂(110110)=011000.

Циклический сдвиг на n разрядов вправо (A:=СR_n(A)) приводит к заполнению n старших разрядов слова значениями n младших разрядов слова. Например, CR₂(110110)=101101, то есть четыре старших разряда 1101 переместились на две позиции вправо, а младшие два разряда 10 переместились на место двух старших разрядов.

Циклический сдвиг на n разрядов влево (A:=СL_n(A)) приводит к заполнению n младших разрядов слова значениями n старших разрядов слова. Например, CL₂(110110)=011011, то есть четыре младших разряда 0110 переместились на две позиции влево, а старшие два разряда 11 переместились на место двух младших разрядов.

Арифметический сдвиг (B:=AR_n(B)), при котором значение старшего разряда дублируется в n старших разрядах. Например, AR₃(100100)=111100, AR₂(100100)=111001.

5. Микрооперации счёта.

В результате их выполнения происходит изменение значения слова на единицу. Микрооперация A:=A+1 называется инкрементированием слова, микрооперация A:=A-1 называется декрементированием слова.

6. Логические микрооперации.

Эти микрооперации присваивают слову значение, получаемое при поразрядном выполнении булевых операций 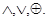Например, 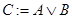. Выполнение логических операций иллюстрируется на рис. 4.6,а, фрагмент схемы ОА, требуемый для выполнения операции 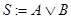, приведён на рис. 4.6,б

 

 

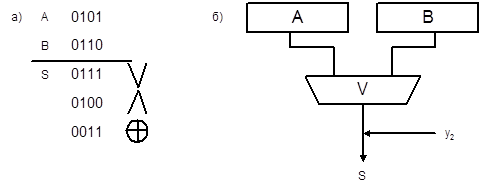
Рис. 4.6. Выполнение логических микроопераций(а) и фрагмент схемы автомата (б)

 

Выполнение микрооперации 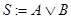инициируется сигналом y₂. Отметим, что для всех остальных ранее рассмотренных микроопераций используются фрагменты схемы OA, аналогичные рис. 4.5, при этом в комбинационной схеме пишется знак соответствующий микрооперации (R₂,L₁,+1 и т.д.).

7. Микрооперация сложения.

Эта микрооперация присваивает слову значение суммы слагаемых. Например, S:=S+A, S:=A+B, 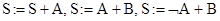. Как видно из этих примеров, приёмник S может служит и источником одного из слагаемых, а значение слагаемых могут инвертироваться. Фрагмент схемы OA для выполнения микрооперации y₃# S:=A+B приведён на рис. 4.7.

 

 

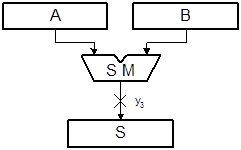
Рис 4.7. Схема OA для выполнения операции сложения

 

Как правило, среди типовых микроопераций нет вычитания S:=A-B, так как вычитание в OA сводится к сложению с обратным знаком S:=A+ (-B). К этому классу относится и микрооперация S:=A+B+1.

8. Комбинированные микрооперации.

Эти микрооперации присущи специализированным устройствами каждая из них содержит несколько действий, присущих микрооперациям классов 1-7. Например, S:=R₁(A+B), S:=R₁(C)+L₂(B). Эти микрооперации не относятся к типовым.

Условимся в дальнейшем сигналы, инициирующие выполнение микроопераций, называть тоже микрооперациями.

Как уже отмечалось ранее, для индикации хода процесса выполнения операции операционным автоматом используются логические условия, образующие множество X={ x₁,…, x_L }. В общем случае, логическое условие - это булева функция y_l (S₁,…,S_I), где S₁,…,S_I - слова информации. Для вычисления логических условий используются комбинационные схемы, задаваемые соответствующими булевыми функциями. Например, x₁ =1, если разряд A[0]=0, приводит к схеме (Рис. 4.8,а), задаваемой функцией 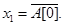Пусть x₂ =1, если значения разрядов A[0] и B[0] совпадают. Очевидно, 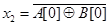, что приводит к схеме (Рис. 4.8,б). Пусть 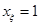, если все разряды слова A равняются нулю. Следовательно, 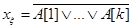, где k-разрядность слова A (Рис. 4.8,в).

 

 

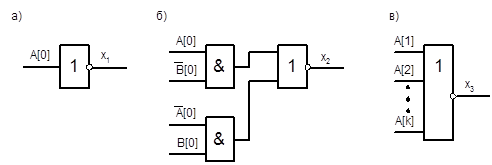
Рис. 4.8. Схемы формирования логических условий

 

При проектировании операционных автоматов удобно представлять алгоритм выполнения операции в виде содержательного графа. Содержательный граф, представленный в терминах микроопераций и логических условий, называется содержательной граф-схемой алгоритма (ГСА).

Граф-схема алгоритма - это ориентированный связный граф, содержащий вершины четырёх типов: начальную, конечную, операторную и условную (Рис. 4.9).

 

 

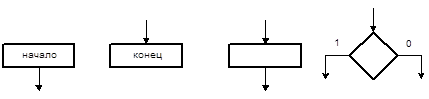
Рис. 4.9. Типы вершин ГСА

 

Начальная вершина не имеет входа и соответствует началу описания алгоритма. Конечная вершина имеет только вход и соответствует окончанию алгоритма. Операторная вершина имеет один вход и один выход, она соответствует одному такту работы автомата. Условная вершина имеет один вход и два выхода, один из которых отмечен символом "1", второй - "0". Один из выходов условной вершины может быть связан с её входом, что недопустимо для операторной вершины. ГСА удовлетворяет следующим условиям:

1. Содержит конечное число операторных и условных вершин, одну начальную и конечную вершину.

2. Входы и выходы вершин соединяются дугами, направленными от выхода ко входу.

3. Каждый выход соединён только с одним входом.

4. Любой вход соединён по крайней мере с одним выходом.

5. Для любой вершины ГСА существует по крайней мере один путь к конечной вершине.

6. В каждой условной вершине записывается одно логическое условие. Выход вершины, отмеченный символом "1", соответствует истинности этого условия, выход, отмеченный символом "0" – ложности.

7. В каждой операторной вершине записывается набор (возможно пустой) одновременно выполняемых микроопераций.

Если все микрооперации ГСА Г относятся к типовым микрооперациям, то такая ГСА называется функциональной. Рассмотрим пример синтеза функциональных ГСА.

Пример 4.1. Синтезировать функциональную ГСА Г₁ для вычисления функции

 

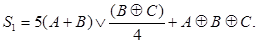
Формирование ГСА является процессом, который трудно формализуется и во многом подобен процессу разработки программ. Функциональная ГСА Г₁ приведена на рис. 4.10.

В процессе разработки ГСА Г₁ выдержано следующее условие - минимизация числа блоков ГСА без введения дополнительных слов. Другими словами - оптимизация быстродействия (каждая операторная вершина соответствует одному регистру памяти OA).

Первая вершина после начальной называется вершиной инициализации и соответствует присвоению словам A,B,C начальных значений d₁, d₂, d₃ ÎD, где D-множество входных слов. Для выполнения операции S₁:=5S₁ используется операция S₁:=4S₁+S₁=L₂(S₁)+S₁. Это связано с отсутствием операций умножения среди типовых микроопераций. Отметим, что микрооперация L_n(A) эквивалентна умножению числа A на 2ⁿ. Например, A=1010₂=10₁₀ L₂(A)=101000₂=40₁₀. Так как 5₁₀=101₂, то 5A=2²×A+2⁰×A=L₂(A)+1. Сдвиг вправо на n разрядов соответствует делению числа на 2ⁿ, поэтому операция B/4 выполняется как R₂(B).

Пример 4.2. Синтезировать функциональную ГСА Г₂ для вычисления функции

 

При разработке ГСА Г₂ как и ранее будем стремиться к минимизации числа блоков без увеличения числа регистров памяти. Обе части выражения S₂ содержат операции A+B и CÅB, которые можно вычислить до проверки условия A>B (Рис. 4.11).

 

 

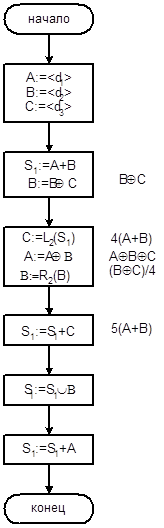
Рис. 4.10. Функциональная граф-схема алгоритма Г₁

 

Задача формирования функциональной ГСА Г является задачей синтеза, для решения которой имеется:

1. Набор типовых микроопераций, который может быть различен для конкретных условий.

2. Критерий эффективности решения, в данном случае оптимизация быстродействия при минимальных затратах оборудования.

3. Формулировка задачи.

Отметим, что процесс синтеза функциональной ГСА является искусством, однако необходимые навыки достаточно просто появляются за счёт тренировок.

 

 

Рис. 4.11. Функциональная граф-схема алгоритма Г₂

 

 

4.3. Типовые структуры операционных автоматов

 

Для решения одной и той же задачи может быть разработано множество операционных автоматов. Для выбора OA, наиболее отвечающего поставленным критериям, используются следующие характеристики:

Производительность. Это среднее число микроопераций, выполняемых за один такт работы. Если память автомата состоит из K регистров, то производительность может находиться в пределах от одного до K. Чем выше производительность, тем сложнее комбинационная схема автомата.

Быстродействие. Это величина, обратная длительности такта автомата, которая зависит от структуры КС и времени срабатывания логических элементов и триггеров регистров. Чем выше быстродействие, тем сложнее КС и/или тем дороже составляющие её компоненты.

Затраты оборудования. Это суммарные затраты оборудования в КС и памяти, она имеет денежное выражение. Чем выше производительность и быстродействие автомата, тем выше и затраты оборудования.

Регулярность. Структура является регулярной, если она состоит из однотипных частей, которые связаны между собой одинаковым образом. Чем выше регулярность, тем проще наладить процесс производства оборудования.

Универсальность. Это возможность реализации достаточно широкого класса алгоритмов без изменения структуры ОА. Чем выше универсальность, тем менее специализирована структура. Универсальный ОА может выполнять любые вычисления, однако производительность вычислений всегда будет ниже, чем для специализированной структуры.

Пусть память ОА состоит из K регистров R₁,…,R_K, выходы которых обозначены S₁,…,S_K соответственно, и пусть каждый регистр содержит n разрядов. Тогда ОА может быть реализован как канонический автомат (Рис. 4.12).

 

Рис. 4.12. Структурная схема канонического автомата

 

Выходы регистров S₁,…,S_K объединены в общую выходную шину разрядности n K, через которую информация подаётся к комбинационным схемам. Комбинационная схема Ф_k формирует новое значение слова S_K (обозначенное как 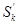), для чего используются слова, образующие множество S_kÍS={S₁,…,S_L} (k =1,…,K). Вычисление слов 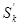происходит под воздействием микроопераций, образующих множество Y^k, причём y^k ÍY является k -м классом разбиения множества Y (k =1,…,K). Комбинационная схема y_l формирует значение логического условия x_l Î x с использованием подмножества S^k+lÍS, где l =1,…,L. По сигналу Clock новые значения слов заносятся в соответствующие регистры через n K-разрядную входную шину. Перед выполнением операции в регистр R_k заносится начальное значение < d_k > слова S_k (k =1,…,K).

Недостаток канонического автомата - избыточность оборудования, что связано с использованием одинаковых элементов (сумматоров, сдвигателей) в разных схемах Ф_k (k =1,…,K). За счёт такой избыточности достигается максимальная производительность (до К микроопераций за один такт) и быстродействие.

Затраты оборудования можно уменьшить, если в одной схеме Ф_k использовать только один сумматор, сдвигатель и т.д. Это приводит к появлению мультиплексоров MX1,…,MXK, подсоединяющих к одному операционному элементу различные слова. Такой подход порождает I-автомат (Рис. 4.13), где I - означает „individual”, то есть для вычислений значений каждого слова используется индивидуальная комбинационная схема.

 

 

Рис. 4.13. Структурная схема I-автомата

 

Каждый из мультиплексоров MX_k управляется микрооперациями из подмножества Y^k и формирует множество слов , поступающих на вход операционных элементов схемы Ф_k (k =1,…,K).

В остальном схема I-автомата ничем не отличается от канонического автомата. Очевидно, что преобразование 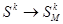требует временных затрат, что приводит к увеличению длительности такта ОА и, следовательно, к уменьшению быстродействия по сравнению с каноническим автоматом.

Число операционных элементов в КС можно свести до минимума, если сделать операционные ресурсы (сумматоры, сдвигатели и т.д.) общими для всех регистров. При этом КС будет включать один сумматор, один сдвигатель и т.д. Такой подход порождает M-автомат (Рис. 4.14), где M - означает „Mutual”, то есть для вычисления значения любого слова используется одна общая комбинационная схема Ф:

 

 

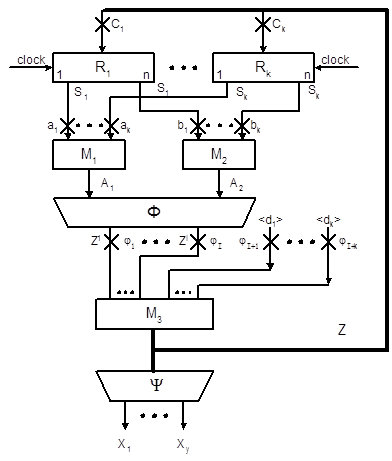
Рис. 4.14. Структурная схема M-автомата

 

Информация из регистра R_k поступает в КСФ либо через мультиплексор M₁ по сигналу a_k, либо через мультиплексор M₂ по сигналу b_k. Комбинационная схема Ф принимает информацию с выхода A₁ и A₂ мультиплексоров и выполняет элементарную обработку информации, формируя выходные значения Z¹,…,Z^I (Например, Z¹:=A₁+A₂, Z²:=R₁(A₁)). Результат выполнения требуемой операции выбирается на шину Z через мультиплексор M₃ по сигналу j_i (i =1,…,I). Начальные значения слов < d₁ >,…,< d_K > поступают на шину Z по сигналу j_I+1,…, j_I+K соответственно. Новые значения слов заносятся в регистры R₁,…,R_K по сигналу C₁,…,C_K соответственно. Логические условия x₁,…, x_y формируются схемой y, при этом y £L. Это связано с тем, что, например, условие x₁ # R₁[0]=1 и x₂ # R₂[0]=1 отображаются одним условием x_j # Z[0]=1. Отметим, что шины A₁,A₂ и Z имеют размерность n, что в K раз меньше размерности шин I-автомата.

Анализ схемы M-автомата показывает, что в каждом такте здесь выполняется только одна микрооперация исходной функциональной ГСА. Следовательно, M-автомат имеет минимальную производительность, что компенсируется высокими регулярностью и универсальностью структуры, а также минимально возможными аппаратурными затратами. Наличие мультиплексора M₃ вносит дополнительную задержку в такт работы M-автомата по сравнению с I-автоматом.

Стремление повысить производительность и сохранить низкие аппаратурные затраты приводит к автоматам, характеристики которых занимают промежуточное значение по сравнению I- и M-автоматами. Такие устройства получили название IM-автоматов, которые разделяются по способу организации комбинационной схемы.

IM-автоматы с параллельной комбинационной схемой (IM_p-автоматы) включают комбинационные схемы Ф₁ для выполнения двухместных микроопераций (сложение, конъюнкция) и Ф₂ для выполнения одноместных микроопераций (инверсия, сдвиг), а также схемы y₁ и y₂ для вычисления логических условий (Рис. 4.15).

IM_p-автоматы можно рассматривать как композицию двух M-автоматов с общей памятью R₁,…,R_K. Первый автомат включает мультиплексоры M₁,M₂,M₄ и схемы Ф₁ и y₁, второй - M₃,M₅,Ф₂ и y₂. Назначение управляющих сигналов a, b, c, d, e, j, y очевидно по аналогии с M-автоматом. При такой организации IM_p-автомат может выполнять одновременно по две микрооперации исходной функциональной ГСА и результаты появляются параллельно на шинах Z₁ и Z₂. Удвоение производительности по отношению к M-автомату связано с введением двух дополнительных мультиплексоров, то есть затраты оборудования в IM_p-автомате больше, чем в M-автоматах.

 

Рис. 4.15. Структурная схема IM-автомата с параллельной комбинационной схемой

 

Очевидно производительность и затраты оборудования в IM_p-автомате растут по мере увеличения числа схем Ф_i. При i =K IM_p-автомат вырождается в I-автомат.

IM_p-автоматы с последовательной комбинационной схемой (IM_s-автоматы) включают три комбинационные схемы Ф₁-Ф_s для выполнения микроопераций и схему y для вычисления логических условий (Рис. 4.16).

 

 

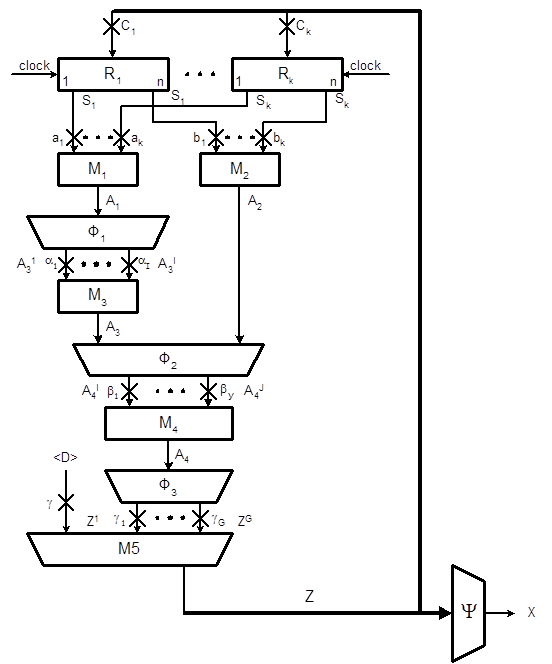
Рис. 4.16. Структурная схема IM-автомата с последовательной комбинационной схемой

 

Информация из регистров S₁,…,S_K попадает через M₁ и M₂ на шины A₁ и A₂. Схема Ф₁ выполняет одноместные микрооперации инверсии слова или некоторых его разрядов. По сигналу a_i (i=1,…,I) через M₃ на шину A₃ передаётся результат выполнения микрооперации a_i (A₁). Схема Ф₂ выполняет двухместные операции, результат которых b_j(A₂,A₃) передаётся на шину A₄. Схема Ф₃ выполняет операции сдвига и формирует окончательный результат выполнения комплексной микрооперации γ_g (b_j (A₂, a_i (A₁))), передаваемый через мультиплексор M₅ на шину Z. Начальные значения для регистров <D>={< d₁ >,…,< d_K >} также передаются через мультиплексор M₅.

Очевидно, IM_s-автомат способен выполнить за один такт до трёх микроопераций функциональной ГСА, что связано с увеличением времени такта по сравнению с M-автоматом. Производительность IM_s-автомата может быть увеличена за счёт увеличения числа уровней в комбинационной схеме. Предельным случаем IM_s-автомата является заказная схема, выполняющая операцию за один такт. Например, для ГСА Г₁ (Рис. 4.10) специализированная схема имеет вид (Рис. 4.17).

 

 

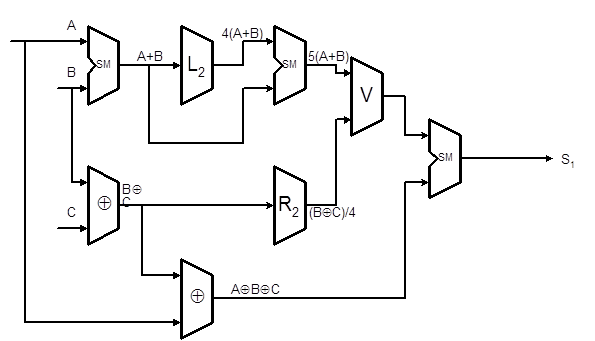
Рис. 4.17 Специализированная схема выполняющая вычисление функции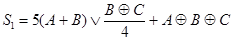

 

Пусть t_S, t_i, t_Sh, t_M, t_R - время выполнения соответствующих микроопераций сумматором, инвертором, сдвигателем, мультиплексором и время записи информации в регистр соответственно. Пусть C_K - затраты оборудования в автомате с канонической структурой, C_M - затраты оборудования для реализации мультиплексора. Тогда характеристики операционных автоматов можно представить следующим образом (Табл. 4.1).

 

Таблица 4.1

Характеристики операционных автоматов

Тип ав- томата	Произ- води-тельность	Затраты оборудо- вания	Длительность такта	Регу-лярность	Универсаль-ность
I	≤ K max	CK+KCM max	tR + tM + tS = tI min	Низкая	Низкая
M	≤ 1 min	CK+3CM min	tI + tM + ty	Высокая	Высокая
IMp	≤ 2	CK+5CM	tI + tM + ty	Высокая	Высокая
IMs	≤ 3	Cmin+5CM	tI +3 tM + ti + tsh + ty Max	Высокая	Высокая

 

Здесь C_min - минимальные затраты оборудования в комбинационной схеме, когда используется один сумматор, один сдвигатель и т.д., t_y - время формирования логических условий схемой y. Время выполнения операции суммирования является максимальным среди всех времён выполнения микрооперации, поэтому при определении длительности такта учитывалось время t_S. Для оценки IM-автоматов в табл. 4.1 рассмотрены классические структуры, приведённые на рис. 4.15 и 4.16.

Отметим, что табл. 4.1 даёт только общую характеристику различных операционных автоматов. Значительное воздействие на все характеристики ОА оказывает функциональная ГСА. Поэтому окончательный выбор структуры ОА может быть сделан только на основании критериев эффективности схемы (например, максимальное быстродействие при заданной стоимости) и анализе функциональной ГСА.

Рассмотрим методы синтеза схем операционных автоматов I, M, IM_p и IM_s, иллюстрируя их на примере ГСА Г₃ (Рис. 4.18)

В ГСА Г₃ каждой элементарной операции обработки информации поставлено в соответствие микрооперация y_n, соответствующая этому действию: y_n ÎY={ y₁,…, y₁₈ }. При этом одинаковым действиям соответствуют одни и те же микрооперации, например, 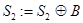везде обозначена как y₉.

Каждой проверке в ГСА сопоставлено отдельное логическое условие, в нашем случае множество X={ x₁, x₂ }.

 

 

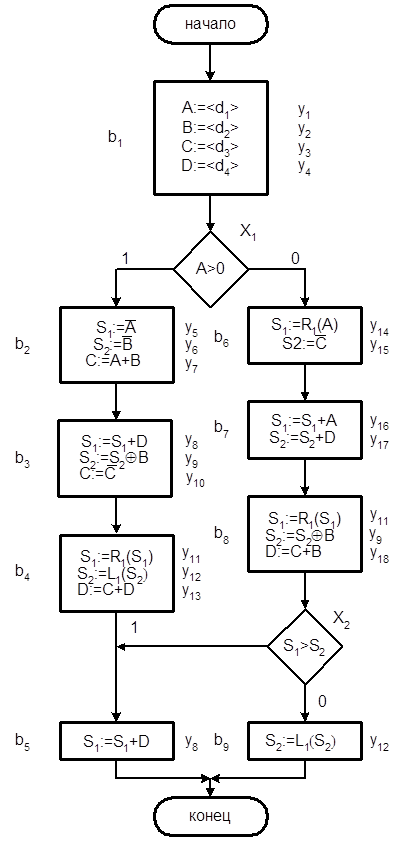
Рис. 4.18. Функциональная граф-схема алгоритма Г₃

Все методы синтеза начинаются с формирования памяти ОА, для чего анализируются типы слов ГСА. Существуют слова трёх типов:

1. Входные слова (тип I) - это слова, для которых выполняются операции инициализации вида S_i:=< d_i >.

2. Выходные слова (тип O) - это результаты выполнения операций.

3. Внутренние слова (тип L) - это слова, значения которых меняются в ходе выполнения алгоритма.

В ГСА Г₃ содержатся слова A (тип IL), B(тип IL), C(тип IL), D(тип IL), S₁(тип OL) и S₂(тип OL). Каждому слову типа L соответствует регистр памяти, разрядность которого совпадает с разрядностью слова. Автоматы, реализующие представленный ГСА Г₃ алгоритм, содержат память, состоящую из шести регистров: RA, RB, RC, RD, RS₁ и RS₂.

 

 

4.4. Синтез I-автоматов

 

Методы синтеза I-автоматов включает следующие этапы.

1. Формирования памяти автомата. В рассматриваемом примере память содержит шесть регистров. Каждому входному слову ставится в соответствие входной полюс автомата, связанный с соответствующим регистром. Каждому выходному слову ставится в соответствие выходной полюс схемы, связанный с соответствующим регистром.

Условимся обозначать I-автомат, схема которого синтезируется по ГСА Г, символом I(Г). Память входные и выходные полюса автомата I(Г₃) показаны на рис. 4.19.

 

 

 

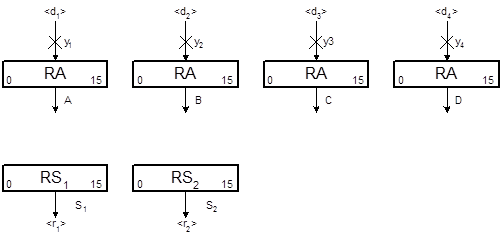
Рис. 4.19. Память автомата I(Г₃)

 

 

Здесь принято, что регистры имеют разрядность n =16. Автомат имеет четыре входных полюса < d₁ >-< d₄ >, информация с которых заносится в регистры по сигналам y₁ - y₄ соответственно, и два выходных полюса <r₁> и <r₄>.

2. Разбиение множества микроопераций на классы эквивалентных микроопераций. Микрооперации y_n, y_m ÎY называются эквивалентными, если они вычисляют новое значение одного итого же слова и относятся к одному классу типовых микроопераций. Например, для микроопераций

 

y₁ # S₁:=A+B,

y₂ # S₁:=R₁(A),

y₃ # S₂:=A+B,

y₄ # S₁:=C+D,

 

только y₁ и y₄ являются эквивалентными. Микрооперации y₁ и y₂ относятся к разным классам типовых микроопераций, а микрооперации y₁ и y₃ имеют разный приёмник информации.

Обозначим разбиение множества Y как П_Y={B₁,…,B_J}, где B_jÎ П_Y - класс эквивалентных микроопераций. Для автомата I(Г₃) П_Y={B₁,…,B₁₃}, где B₁={ y₁ },…, B₄={ y₄ }, B₅={ y₅ }, B₆={ y₆, y₁₅ },B₇={ y₇ }, B₈={ y₈, y₁₆ }, B₉={ y₉ }, B₁₀={ y₁₀ }, B₁₁={ y₁₁, y₁₄ }, B₁₂={ y₁₂, y₁₇ }, B₁₃={ y₁₃, y₁₈ }. Микрооперации y₁₂ и y₁₇ помещены в один блок, так как сдвиг влево сводится к сложению L₁(S₂)=S₂+S₂.

3. Формирование обобщённых операторов. Обобщённый оператор - это специальная форма представления эквивалентных микроопераций. Например, микрооперации y₁ # S₁:=A+B и y₂ # S₁:=C+D, могут быть представлены обобщённым оператором S₁:=A₁+A_2, где

 

 

 

 

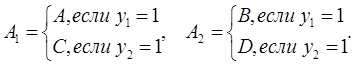
Этому оператору соответствует схема (Рис. 4.20,а), где выражение A₁ и A₂ реализуются мультиплексорами.

 

 

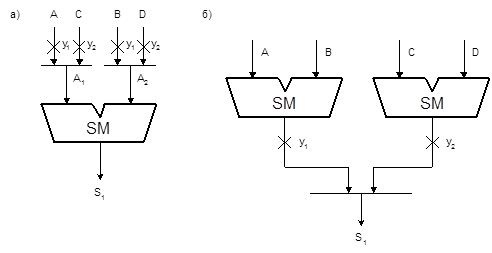
Рис. 4.20. Реализация эквивалентных микроопераций с обобщёнными операторами(а) и без них(б)

 

Такой подход позволяет уменьшить число дорогостоящих операционных элементов, в данном случае - сумматоров. При реализации микроопераций y₁ и y₂ без использования обобщённых операторов схема включает два сумматора (Рис. 4.20,б). Выражение для A₁ может быть записано как .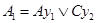

Для автомата I(Г₃) имеем: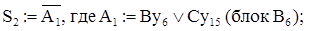

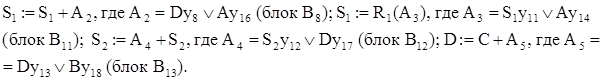
4. Разбиение множества микроопераций по признаку результирую-щих слов. Представим множество Y в виде объединения множеств Y_SÍY, соответствующих микрооперациям, вычисляющим новое значение слова S. В нашем случа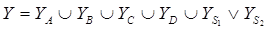е , где

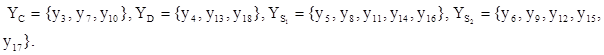
5. Синтез комбинационной схемы автомата. Каждому множеству Y_S, полученному на предыдущем этапе соответствует часть комбинационной схемы. Если множество Y_S включает более одного элемента, то выходы соответствующих операционных элементов поступают на мультиплексор. Например, классу Y_D соответствует подсхема (Рис. 4.21). Так как микрооперациям y₁₃ и y₁₈ соответствует обобщённый оператор, то он использован при синтезе схемы. Микрооперация y ₄ относится к микрооперациям инициализация и её реализация показана на рис. 4.19.

Рис. 4.21. Фрагмент подсхемы для множества Y_D

 

Объединение подсхем для всех множеств Y_SÍY в одну комбинационную схему и её связь с памятью позволяют получить схему автомата (Рис. 4.22).

 

Рис. 4.22. Функциональная схема автомата I(Г₃)

В эту схему входят и две комбинационные схемы, формирующие логические условия x₁ # A>0 и x₂ # S₁>S₂.

Оценим характеристики этой схемы: E_I(Г) - производительность при реализации алгоритма Г; Q_I(Г) - затраты оборудования при реализации алгоритма Г; T_I(Г) - длительность такта при реализации алгоритма Г; Ф_I(Г) - время выполнения алгоритма Г.

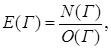Производительность любого автомата Е(Г) можно оценить по формуле

(4.1)

 

 

где N(Г) - суммарное число микроопераций в операционных вершинах ГСА Г, О(Г) - число операционных вершин. Для автомата I(Г₃) имеем N(Г)=22, О(Г)=9, следовательно E_I(Г₃)=2,44.

Затраты оборудования проще всего оценить в денежном исчислении, однако это можно сделать и в условных единицах. Примем затраты оборудования в сумматоре за единицу, а в остальных операционных элементах за 0.1. Схема I(Г₃) включает 4 сумматора, 3 инвертора, один сдвигатель, один сумматор по модулю два и 3 мультиплексора. Таким образом, Q_I(Г₃)=4,8. Так как память у всех автоматов одинакова, то она не принимается во внимание при оценки О_I(Г).

Для определения времени такта необходимо знать время переключения каждой схемы. Пусть t - время переключения схемы И-НЕ. Причем, что время переключения сумматора t_S =20 t, а время переключения сдвигателя t_sh, инвертора t_I и мультиплексора t_M равняется 2 t, время переключения триггера t_r - 6t. Для I-автомата

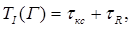
(4.2)

 

где t_кс =max(t_s, t_sh, t_I)+2 t_M = t_S +2 t_M - время переключения комбинационной схемы. Для рассматриваемого примера T_I(Г₃)=22 t +6 t =30 t.

Для определения Ф_I(Г) необходимо найти среднее число тактов работы автомата при выполнении алгоритма Г- n_I (Г), и затем умножить n_I (Г) на T_I(Г). Параметр n_I (Г) можно найти статистически, многократно моделируя выполнение алгоритма при разных начальных данных. Этот параметр можно считать, используя следующую процедуру:

1. Найти все пути a₁,…, a_y, ведущие из начальной ГСА в конечную.

2. Для пути a_j найти число входящих в него операционных вершин n_j (j=1,…,J).

3. Определить параметр n (Г)= n₁ +…+ n_J.

4. Разделить n (Г) на J, полученный результат даёт параметр n_I (Г).

 

 

Итак, время выполнения алгоритма можно определить по формуле