 |
Сигнал, отраженный от поверхности и регистрируемый приемником
|
|
|
|
Комплексная амплитуда поля точечного излучателя, находящегося в нижнем полупространстве, принимаемая антенной
Рассмотрим точечный отражатель, расположенный в нижнем полупространстве и имеющий координаты 
. Будем отраженное от него поле в плоскости 
описывать функцией
,(9)
где 
задается выражением (8).
Спектр плоских волн для распределения комплексной амплитуды (9), вычисленный с использованием (2) будет иметь вид
.(10)
Распространяясь до плоскости 
, спектр трансформируется согласно
.(11)
После прохождения границы раздела, каждая плоская волна должна быть умножена на коэффициент прохождения Френеля при распространении снизу вверх, таким образом, что спектр плоских волн в плоскости 
принимает вид
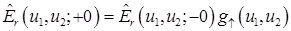,(12)
где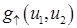 
– коэффициент прохождения Френеля для плоской волны, характеризуемой парой 
.
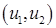Распределение комплексной амплитуды поля в плоскости 
будет находиться как обратное преобразование Фурье от спектра, задаваемого выражением (12)
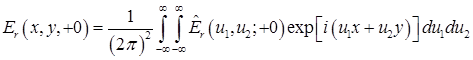.(13)
Принимаемый апертурой антенны, центр которой имеет координаты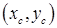 
, сигнал записывается как
.(14)
Подстановка (13) в (14) приводит к такому выражению для комплексного выхода с антенны
(15)
в котором
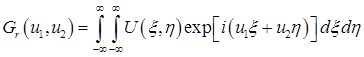(16)
– обратное преобразование Фурье от распределения комплексной амплитуды по апертуре антенны.
Комплексный выход 
с антенны радиолокатора, центр апертуры которой имеет координаты 
, при отражении от точечного рассеивателя, координаты которого задаются вектором 
, может быть записан следующим образом
,(17)
где 
– комплексный коэффициент отражения от элементарной площадки заглубленного предмета.
Сигнал, отраженный от поверхности и регистрируемый приемником
|
|
|
Найдем регистрируемый приемником сигнал, который получается в результате отражения от поверхности раздела. Для этого сначала запишем выражение для спектра плоских волн после отражения от поверхности раздела, которое будет произведением (1) и коэффициента отражения Френеля 
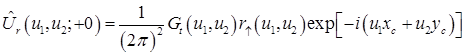. (18)
Спектру (18) соответствует связанное с ним обратным преобразованием Фурье распределение комплексной амплитуды поля
(19)
Комплексный выход антенны будет найден интегрированием (19) по апертуре антенны
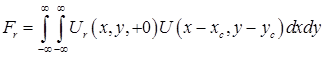.(20)
Выполняя подстановку (18) и (19) в (20), осуществляя интегрирование, получается следующее выражение для комплексного выхода антенны, обусловленного отражением от поверхности раздела
.(21)
В полученном выражении комплексное число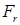 
, как и следовало ожидать, не зависит от координат центра апертуры. Величина 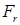зависит от комплексной диэлектрической проницаемости нижнего полупространства через коэффициент отражения Френеля и является постоянным слагаемым, которое, наряду с опорным сигналом от передатчика к приемнику, добавляется к сигналу, регистрируемому радиолокатором после отражения от рассеивателей, находящихся в нижнем полупространстве.
Коэффициенты прохождения и отражения Френеля для плоской волны
Найдем коэффициенты Френеля для отражения и прохождения плоской волны, задаваемой уравнением
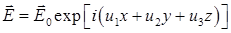, (22)
в котором величины 
, 
и 
в общем случае могут быть комплексными и не иметь смысла проекций волнового вектора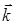 
на оси координат. В таком случае уравнение (22) будет описывать как однородную, так и неоднородную волну, в которой направление убывания амплитуды и направление распространения могут не совпадать [10]. Подстановка (22) в уравнение Гельмгольца, записанного для однородной среды вне области, занятой источниками
|
|
|
, (23)
в котором
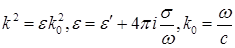, (24)
позволяет получить условие, которое должно выполняться для величин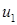 
, 
и в общем случае
. (25)
В предыдущих параграфах, плоская волна и соответствующие ей коэффициенты отражения и преломления характеризовались парой чисел 
и , а не с помощью угла падения или скольжения, поскольку для удобства последующих расчетов, с применением быстрого алгоритма преобразования Фурье, удобно поступить именно так. Найдем соответствующие коэффициенты отражения и преломления как функции и , т.е. именно в таком виде, в котором они фигурируют в формулах из предыдущих параграфов.
Рис. 2. К выводу френелевских коэффициентов отражения и прохождения для однородных и неоднородных плоских волн.
Пусть на поверхность раздела падает плоская волна, задаваемая уравнением (23) (рис. 2). Решение задачи будем искать в виде трех волн: падающей и отраженной в верхнем полупространстве и преломленной в нижнем полупространстве, причем отраженную и преломленную плоские волны запишем в виде
, (26)
. (27)
В формулах (26) и (27) векторы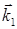 
, 
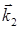в общем случае являются комплексными.
На границе раздела двух сред должны удовлетворяться граничные условия [10]
(28)
В выражении для граничных условий (28) первый встречающийся индекс обозначает среду: 1 – верхнее полупространство, 2 – нижнее; индекс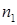 
, 
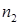– обозначают проекцию на нормаль, проведенную в верхнюю и нижнюю среду соответственно; индекс 
– обозначает проекцию на касательный к границе раздела вектор.
Для комплексных амплитуд горизонтальной поляризации отраженной и прошедшей волн получаются следующие выражения
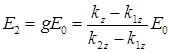, (29)
, (30)
в которых 
– компоненты комплексного волнового вектора в каждой среде связаны с и соотношениями аналогичными (25). Индекс при этом обозначает третью компоненту в соответствующей среде. Таким образом, могут быть получены следующие формулы для коэффициентов прохождения и отражения для любого типа плоских волн
,(31)
,(32)
в которых знаки перед корнями должны выбираться с учетом требуемых проекций – компонент волновых векторов на оси координат.
|
|
|
|
|
|
