 |
Краткие теоретические сведения
|
|
|
|
Лабораторная работа №2
Исследование трехфазной цепи при соединении приемников в звезду
Цель работы – исследование трех однофазных приемников, соединенных в звезду с нейтральным и без нейтрального провода при различных режимах работы цепи.
Краткие теоретические сведения
Трехфазная цепь представляет собой совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, амплитуды, сдвинутые друг относительно друга на 1200 и создаваемые общим источником энергии. Такая трехфазная система называется симметричной. Каждую цепь трехфазной системы, характеризующуюся одним током, называют фазой.
Трехфазные цепи имеют ряд преимуществ перед однофазными цепями: возможность получения от одного генератора двух различных эксплуатационных напряжений – фазного и линейного; экономичность передачи энергии на дальние расстояние (экономится цветной металл на изготовление ЛЭП); возможность получения вращающегося магнитного поля, необходимого для работы электродвигателей переменного тока.
Трехфазная цепь состоит их трех основных частей: трехфазного генератора, линии передачи и приемников.

Рис. 1. Условные обозначения обмоток трехфазных генераторов
Фазы трехфазного генератора (см. рис. 1), приемника могут соединяться звездой (λ) или треугольником (Δ).
Звездой называют соединение, при котором концы фаз генератора X, Y, Z или приемника x, y, z соединяются в один большой узел N или n, называемый нейтральной точкой или нейтралью генератора или приемника (см. рис. 2). Провод N-n, соединяющий нейтральные точки генератора и приемника, называют нейтральным или нулевым.
|
|
|
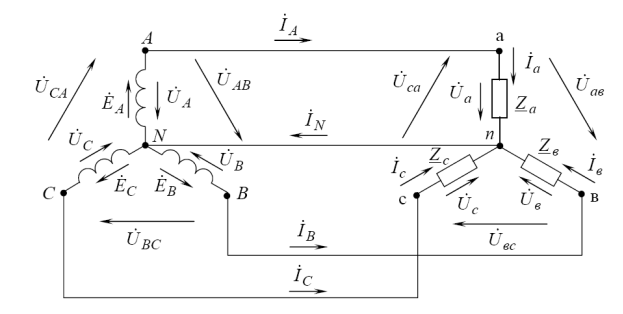
Рис. 2. Схема четырехпроводной трехфазной цепи
Звезду с нейтральным проводом называют четырехпроводной, а без нейтрального провода – трехпроводной. Провода, соединяющие начала фаз генератора и приемника, называют линейными. По линейным проводам A-a, B-b, C-c протекают линейные токи IA, IB, IC. В фазах генератора и приемника протекают фазные токи Ia, Ib, Ic. Фаза генератора, линейный провод и фаза приемника соединяются последовательно, поэтому линейный ток одновременно является фазным: IA= Ia, IB= Ib, IC= Ic, т.е.
IЛ = IФ (1)
Уже отмечалось. Что важной особенностью трехфазных цепей является наличие двух напряжений – фазного и линейного.
Фазным UФназывают напряжение между началом и концом каждой фазы генератора или приемника.
UA, UB, UC – фазные напряжения генератора.
Ua, Ub, Uс - фазные напряжения приемника.
Линейным UЛназывают напряжение между началами двух фаз.
UAB, UBC, UCA – линейные напряжения.
Соотношения между линейными и фазными напряжениями можно определить из уравнений, составленных по второму закону Кирхгофа для контуров ANBA, BNCB, CNAC (рис. 2).
ŮAB=ŮA - ŮB
ŮBC=ŮB - ŮC (2)
ŮCA= ŮC - ŮA
На рис. 3.а и 3.б представлены векторная и топографическая векторная диаграмма фазных и линейных напряжений, построенных по этим уравнениям.
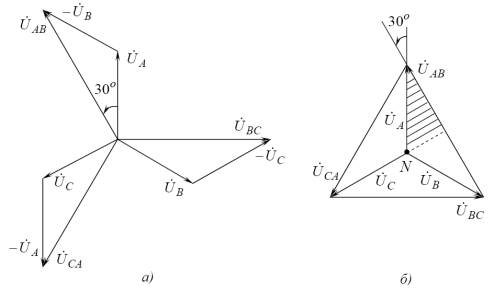
Рис. 3. Векторная (а) и топографическая векторная (б) диаграммы напряжений трехфазного генератора.
Из диаграммы напряжений на рис. 3.а можно определить как количественные, так и фазовые соотношения между фазными линейными напряжениями симметричной системы. Векторы линейных напряжений ŮAB, ŮBC, ŮCA, сдвинуты относительно друг друга на 1200 и опережают соответственно векторы фазных напряжений ŮA, ŮB, ŮC на 300. Из заштрихованного треугольника следует:
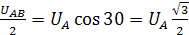 ;
;  т.е.
т.е.  (3)
(3)
ГОСТом предусмотрены линейные и фазные напряжения, связанные соотношением (3) для цепей низкого напряжения:
UФ=127В, UЛ=127 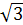 =220В;
=220В;
|
|
|
UФ=220В, UЛ=220 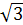 =380В;
=380В;
UФ=380В, UЛ=380 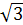 =660В.
=660В.
Ůа= ŮА, Ůв=ŮВ, Ůс=ŮС.
Если комплексные сопротивления фаз приемника равны соответственно Z a, Z в, Z c, то токи в каждой фазе можно определить по закону Ома:
İа= 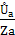 İв=
İв= 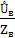 İc=
İc= 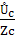 (4)
(4)
На схеме рис. 2. Показаны условно положительные направления, принятые для всех токов и напряжений трехфазной цепи. В соответствии с первым законом Кирхгофа для узла «n» ток в нейтральном проводе
İn= İa+ İb+ İc (5)
В трехфазной цепи различают основные режимы работы.
1. Симметричный режим, при котором комплексные
сопротивления фаз трехфазных приемников равны между собой: Z a= Z b= Z c, т.е Ra=Rb=Rc и Xa=Xb=Xc. Токи в фазах будут равны между собой Ia= Ib= Ic
и сдвинуты по фазе относительно соответствующих фазных напряжений на один и тот же угол φa=φb=φc.
На рис. 4.а изображена векторная диаграмма фазных напряжений и токов для случая, когда нагрузка каждой фазы приемника носит активно-индуктивный характер, например электродвигатель.
Из векторной диаграммы рис. 4.б видно, что геометрическая сумма всех токов равна нулю
İa+ İb+ İc=0
Из сравнения (5) и (6) следует, что İn=0.
Отсюда вывод: при симметричной нагрузке фаз ток в нейтральном проводе отсутствует, поэтому необходимость в нем отпадает. Получается трехпроводная цепь. В нее включаются симметричные трехфазные приемники, например, трехфазные электродвигатели, электрические печи.
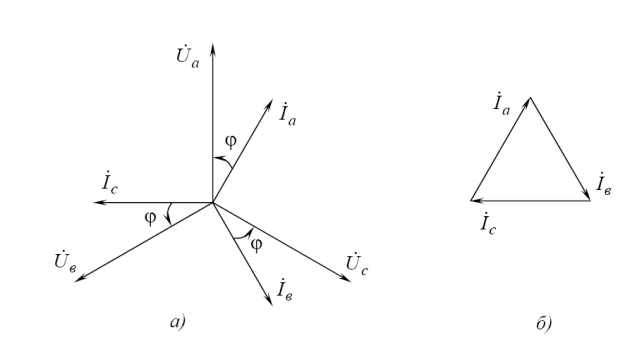
Рис. 4
2. Несимметричный режим, при котором комплексные
сопротивления фаз не равны между собой Z a≠ Z b≠ Z c.
В цепи с нейтральным проводом фазные напряжения приемника равны фазным напряжениям генератора, поэтому изменение режима работы одной из фаз не оказывает влияния на режим работы двух других фаз. Нейтральный провод обеспечивает равенство фазных напряжений приемника при несимметричной нагрузке. Для несимметричного приемника векторы токов уже не образуют симметричную систему и ток в нейтральном проводе
İn= İa+ İb+ İc ≠0.
В четырехпроводную цепь включают однофазные несимметричные приемники (лампы накаливания).
При включении несимметричных приемников в трехпроводную трехфазную цепь из-за разных потенциалов точек N и n между ними возникает напряжение UnN, называемое напряжением между нейтралями. В этом случае векторы фазных напряжений приемника образуют несимметричную систему (см. рис. 5.) и определяют из соотношений:
|
|
|
Ůa= ŮA - ŮnN, Ůb= ŮB – ŮnN, Ůc= ŮC – ŮnN.
Напряжение UnN определяется по формуле междуузлового напряжения, т.к. трехпроводная цепь представляет собой схему с двумя узлами n и N:

где 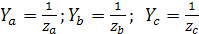 - комплексные проводимости фаз.
- комплексные проводимости фаз.
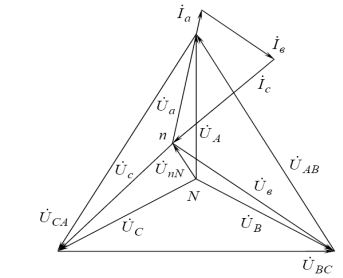
Рис. 5. Векторная диаграмма напряжений и токов несимметричного приемника без нейтрального провода
Токи при этом образуют также несимметричную систему, но вследствие смещения нейтрали приемника их векторная сумма (см. рис. 5) равна нулю.
İa+ İb+ İc=0
где İa= Y aŮa; İb= Y bŮb; İc= Y cŮc.
При несимметричной нагрузке в случае обрыва нейтрального провода величина UnN будет максимальной и на фазах нагрузки могут возникнуть значительные перенапряжения. По этой причине плавкий предохранитель не включают в нейтральный провод.
Активная мощность каждой фазы определяется по формуле:

Активная мощность трехфазного приемника равна арифметической сумме активных мощностей отдельных фаз

Активная мощность симметричного трехфазного приемника:
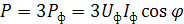
Аналогично выражается и реактивная мощность:


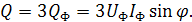
Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через UЛ и IL.
При соединении мощность симметричного трехфазного приемника будет равна:

Программа работы
1. Исследовать трехфазную четырехпроводную и трехпроводную цепи при соединении приемников в звезду при симметричном и несимметричном режимах.
2. Для каждого режима определить активную и реактивную мощность каждой фазы и всей цепи.
3.Определить отношение 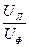 для симметричной нагрузки и для несимметричных нагрузок с нейтральным проводом.
для симметричной нагрузки и для несимметричных нагрузок с нейтральным проводом.
4. Построить векторные диаграммы напряжений и токов для всех режимов.
5.Определить ток нейтрального провода из векторной диаграммы и сравнить его с измеренной величиной.
Электрическая схема

Рис.6. Схема трехфазной цепи при соединении фаз приемников в звезду
|
|
|
S1, S2, S3, S4 - выключатели; А1, A2, A3, А4 - амперметры с номинальным значением тока 5А; Rl. R2, R3 - переменные резисторы; V - переносной вольтметр c номинальным значением напряжения 300В.
Таблицы данных
Таблица 1
| Режим работы цепи | Измеряемые величины | Расчетные величины | ||||||||||||||||
| 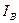
| 
| 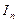
| 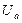
| 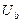
| 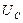
| 
| 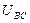
| 
| 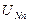
| 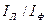
| 
|  С С
| 
| 
| 
| ||
| А | А | А | A | B | B | B | B | B | B | B | - | Вт | Вт | Вт | Вт | вар | ||
| Симметричный | С нейтральным проводом | |||||||||||||||||
| Без нейтрального провода | ||||||||||||||||||
| Несимметричный | С нейтральным проводом | 1.6 | 2.5 | 0.5 | ||||||||||||||
| Без нейтрального провода | 1.8 | 2.2 |
Вычисления к таблице 1
1. Симметричный режим работы цепи:
1.1. С нейтральным проводом:
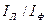 =0;
=0;
Активная мощность каждой фазы определяется по формуле: 
При 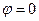 :
: 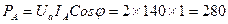 Вт;
Вт;  Вт;
Вт;

|

|
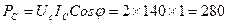 Вт;
Вт;
Активная мощность трехфазного приемника равна арифметической сумме активных мощностей отдельных фаз:  ;
;
 =840 Вт;
=840 Вт;
Реактивная мощность:
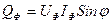 ;
; 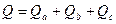 ;
;
Так как 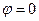 , то
, то 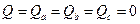 ;
;
1.2. Без нейтрального провода:
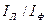 =0;
=0;
При 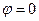 :
:  ;
;  Вт;
Вт;

|

|
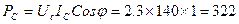 Вт;
Вт;
 =996 Вт;
=996 Вт;
Так как 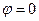 , то
, то 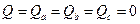 ;
;
2. Несимметричный режим работы цепи:
2.1. С нейтральным проводом:
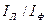 =0;
=0;
При 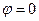 :
: 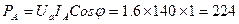 Вт;
Вт;  Вт;
Вт;

|

|
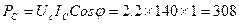 Вт;
Вт;
 =812 Вт;
=812 Вт;
Так как 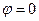 , то
, то 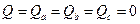 ;
;
2.2. Без нейтрального провода:
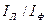 =0;
=0;
При 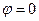 :
: 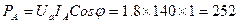 Вт;
Вт;  Вт;
Вт;

|

|
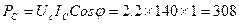 Вт;
Вт;
 =840 Вт;
=840 Вт;
Так как 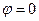 , то
, то 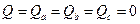 ;
;
Ответы на контрольные вопросы
|
|
|


