 |
Имеется магнитоэлектрический механизм преобразования с внутренним сопротивлением
|
|
|
|
Задача № 1.1,б.
При измерении частоты сигнала  были получены следующие результаты наблюдений
были получены следующие результаты наблюдений  :
:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  кГц.
кГц.
Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.
Определить: результат измерения частоты  , значение среднеквадратического отклонения результатов наблюдений
, значение среднеквадратического отклонения результатов наблюдений  (исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения
(исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения 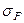 , указать его доверительную вероятность
, указать его доверительную вероятность  ; интервал случайных погрешностей
; интервал случайных погрешностей  с доверительной вероятностью
с доверительной вероятностью  .
.
· Рассчет результата измерения частоты  .
.

 кГц.
кГц.
· Рассчет среднеквадратического отклонения результатов наблюдений  .
.
 , где
, где  – абсолютная погрешность
– абсолютная погрешность  -го измерения.
-го измерения.


 кГц.
кГц.
С целью установления промахов воспользуемся правилом «трех сигма» – если  , то такой результат не является промахом.
, то такой результат не является промахом.  . Результаты вычислений представлены в таблице 1.
. Результаты вычислений представлены в таблице 1.
Таблица 1
 , кГц , кГц
| 18.305 | 18.308 | 18.312 | 18.309 | 18.304 | 18.306 | 18.310 | 18.303 |
 , кГц , кГц
| 0.006 | 0.008 | 0.004 | 0.007 | 0.005 | 0.007 | 0.006 | 0.004 |
Т.к. во всех случаях выражение  больше нуля, то можно заключить, что грубых погрешностей нет.
больше нуля, то можно заключить, что грубых погрешностей нет.
· Рассчет среднеквадратической погрешности результата измерения 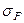 .
.
 кГц.
кГц.
· Рассчет доверительной вероятности  .
.
 , где
, где  ,
,  .
.
После замены  получаем следующее:
получаем следующее:

 .
.
· Рассчет равновероятного интервала случайных погрешностей.
Т.к. число измерений мало ( ), то для нахождения интервала случайных погрешностей воспользуемся распределением Стьюдента, согласно которому
), то для нахождения интервала случайных погрешностей воспользуемся распределением Стьюдента, согласно которому  . Для заданных доверительной вероятности
. Для заданных доверительной вероятности  и числа наблюдений
и числа наблюдений  , табулированное значение коэффициента Стьюдента
, табулированное значение коэффициента Стьюдента  . Следовательно:
. Следовательно:
 кГц.
кГц.
Задача 1.1г
При измерении частоты сигнала F получены следующие результаты наблюдений Fi: 18.305, 18.308, 18.312, 18.309, 18.304.
|
|
|
Считать что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.
Определить результат измерения частоты F, значение среднеквадратического отклонения результатов наблюдений σ (исключить, если имеются промахи) значение среднеквадратичной погрешности результата измерения σF указать его доверительную Вероятность P; интервал случайных погрешностей ±ΔP с доверительной вероятностью P = 0.95.
Решение:
Условно результатом измерения частоты будем считать, усреднение всех результатов по времени 
Определим абсолютное отклонение:
| Частота | Абсолютное отклонение |
| 18.305 | -0.03 |
| 18.308 | 0.00 |
| 18.312 | 0.04 |
| 18.309 | 0.01 |
| 18.304 | -0.04 |
Среднеквадратическое отклонение.
По определению среднеквадратичное отклонение это есть 
Находим несмещенную оценку среднеквадратичного отклоненного.


Находим оценку среднеквадратичного отклонения. 
Оценим уровень значимости коэффициентов

Откидываем все которые меньше единицы, находим соответственно


Задача 1.1 д.
При измерении частоты сигнала  были получены следующие результаты наблюдений
были получены следующие результаты наблюдений  :
:  ,
,  ,
,  ,
,  ,
,  кГц.
кГц.
Считать, что генеральная совокупность отклонений результатов наблюдений распределена по
нормальному закону.
Определить: результат измерения частоты  , значение среднеквадратического отклонения результатов наблюдений
, значение среднеквадратического отклонения результатов наблюдений 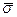 (исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения
(исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения  , указать его доверительную вероятность
, указать его доверительную вероятность  ; интервал случайных погрешностей
; интервал случайных погрешностей  с доверительной вероятностью
с доверительной вероятностью  .
.
Решение:
Определим результат измерения частоты:
 кГц
кГц
Определим значение СКО результатов наблюдений:

Исключим промахи:
а) Расположим результаты наблюдения в порядке возрастания:

б) Рассчитаем специальные коэффициенты:


в) Определим граничное значение коэффициентов:
|
|
|
 - уровень значимости.
- уровень значимости.
 - количество наблюдений.
- количество наблюдений.

Так как  и
и  , то промахов нет.
, то промахов нет.
Определим значение среднеквадратической погрешности результата измерения:

Расчет доверительной вероятности:

Определим интервал случайных погрешностей:
 кГц
кГц
Задача 1.2 г
Проводится проверка рабочего вольтметра. Для этого источником напряжения многократно устанавливается на нём одно и то же проверяемое напряжение  В. Действительные значения
В. Действительные значения  каждый раз определяются по образцовому вольтметру. Получены следующие значения
каждый раз определяются по образцовому вольтметру. Получены следующие значения  : 149.8, 150.7, 151.7, 149.4, 150.0, 159.9, 150.8, 150.7, 151.3, 151.4.
: 149.8, 150.7, 151.7, 149.4, 150.0, 159.9, 150.8, 150.7, 151.3, 151.4.
Определить систематическую составляющую погрешности  , интервал случайной погрешности
, интервал случайной погрешности  с доверительной вероятностью
с доверительной вероятностью  для поверяемого вольтметра. В процессе обработки показаний исключить промахи, если они имеются. Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.
для поверяемого вольтметра. В процессе обработки показаний исключить промахи, если они имеются. Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.
Решение:
1) Исключение систематической погрешности
 В, где
В, где 
2) Оценка результатов измерений
 В
В
3) Оценка абсолютной погрешности каждого наблюдения

 , В , В
| 0,2 | -0,7 | -1,7 | 0,6 | -9,9 | -0,8 | -0,7 | -1,3 | -1,4 |
4) Нахождение СКО
 В
В
5) СКО оценки результатов измерений
 В
В
6) Исключение промахов
Упорядочим результаты наблюдений по возрастанию
 , В , В
| 149,4 | 149,8 | 150,7 | 150,7 | 150,8 | 151,3 | 151,4 | 151,7 | 159,9 |

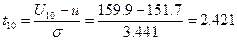
По таблице находим, что  для данного случая равно 2,54.
для данного случая равно 2,54.  и
и  меньше чем
меньше чем  , следовательно промахов нет.
, следовательно промахов нет.
7) Определение границ доверительного интервала
По таблице определим  , тогда доверительный интервал
, тогда доверительный интервал  В.
В.
Отклонение результатов измерений не превышает по модулю 3,59 В с вероятностью 0,99.
Задача 1.3
При измерении резонансной частоты  контура с помощью образцового измерительного генератора и индикатора резонанса получены следующие результаты наблюдений
контура с помощью образцового измерительного генератора и индикатора резонанса получены следующие результаты наблюдений  : 8.935, 8.924, 8.910, 8.930, 8.937,8.920,8.941,8.923,8.918,8.929 кГц.
: 8.935, 8.924, 8.910, 8.930, 8.937,8.920,8.941,8.923,8.918,8.929 кГц.
Значения с нечетными номерами получены при подходе к  со стороны меньших значений частоты, четные со стороны больших значений.
со стороны меньших значений частоты, четные со стороны больших значений.
Чему равен результат измерения частоты  , вариация показаний В, интервал случайной погрешности ±ΔP с доверительной вероятностью P = 0.90 при нормальном законе распределения случайных отклонений.
, вариация показаний В, интервал случайной погрешности ±ΔP с доверительной вероятностью P = 0.90 при нормальном законе распределения случайных отклонений.
Решение:
|
|
|
Условно результатом измерения резонансной частоты  будем считать, усреднение всех результатов по времени
будем считать, усреднение всех результатов по времени 
1.4 При одновременных наблюдениях тока  и напряжения
и напряжения  получены следующие значения:
получены следующие значения:

| 50.15 | 50.21 | 50.17 | 50.18 | 50.25 | 50.20 | 50.24 | 50.25 | 50.20 | |

| 70.37 | 70.42 | 70.35 | 70.39 | 70.43 | 70.41 | 70.43 | 70.44 | 70.40 | 70.36 |
Определить результат измерения тока  , напряжения
, напряжения  , коэффициент корреляции между их случайными отклонениями
, коэффициент корреляции между их случайными отклонениями  и
и  (учитывать только связь между одновременными наблюдениями).
(учитывать только связь между одновременными наблюдениями).
Решение:

|  , мА , мА
| 
|  , мВ , мВ
| 
| 
| 
|
| 50.15 | 0.050 | 70.37 | 0.030 | 2.500×10-4 | 9.000×10-4 | |
| 50.21 | -0.010 | 70.42 | -0.020 | 1.000×10-4 | 4.000×10-4 | |
| 50.17 | 0.030 | 70.35 | 0.050 | 9.000×10-4 | 2.500×10-3 | |
| 50.18 | 0.020 | 70.39 | 0.010 | 4.000×10-4 | 1.000×10-4 | |
| 50.25 | -0.050 | 70.43 | -0.030 | 2.500×10-3 | 9.000×10-4 | |
| 50.20 | 0.000 | 70.41 | -0.010 | 0.000 | 1.000×10-4 | |
| 50.24 | -0.040 | 70.43 | -0.030 | 1.600×10-3 | 9.000×10-4 | |
| 50.25 | -0.050 | 70.44 | -0.040 | 2.500×10-3 | 1.600×10-3 | |
| 50.20 | 0.000 | 70.40 | 0.000 | 0.000 | 0.000 | |
| 50.15 | 0.050 | 70.36 | 0.040 | 2.500×10-3 | 1.600×10-3 |
 ;
;  случайные отклонения результата наблюдения тока и напряжения соответственно.
случайные отклонения результата наблюдения тока и напряжения соответственно.
 ;
;  .
.
Доверительный интервал определим с доверительной вероятностью  . Для выдранной доверительной вероятности коэффициент Стьюдента равен
. Для выдранной доверительной вероятности коэффициент Стьюдента равен  . Определим границы доверительного интервала:
. Определим границы доверительного интервала:
 ;
;  .
.
Результат измерения напряжения и тока:
 ;
;  ;
;  .
.
Найдем коэффициент корреляции, используя следующею формулу:
 .
.
Задача № 1.6.
Проведено измерение частоты  кГц с погрешностью в интервале
кГц с погрешностью в интервале  кГц с доверительной вероятностью
кГц с доверительной вероятностью 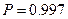 .
.
Чему равны равновероятные интервалы  (
( ) при равномерном и нормальном законах распределения случайных погрешностей?
) при равномерном и нормальном законах распределения случайных погрешностей?
· Рассчет равновероятного интервала при равномерном законе распределения погрешностей:
 Все возможные случайные погрешности результата измерений расположены в интервале
Все возможные случайные погрешности результата измерений расположены в интервале  , где
, где  – максимальная погрешность. Вероятность того, что случайная величина
– максимальная погрешность. Вероятность того, что случайная величина  попадет в интервал
попадет в интервал  , равна
, равна  .
.
Рисунок 1 – График равномерного закона
распределения плотности вероятности.
Из условия задачи известно, что такая вероятность 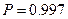 при
при  . Следовательно,
. Следовательно,  кГц. Тогда для вероятности
кГц. Тогда для вероятности  :
:
 , и интервал
, и интервал  кГц.
кГц.
|
|
|
· Рассчет равновероятного интервала при нормальном законе распределения погрешностей:
Из условия задачи известно, что  , где
, где  – табулированный интеграл вероятностей,
– табулированный интеграл вероятностей,  ,
,  кГц. Находим
кГц. Находим  , соответствующее вероятности
, соответствующее вероятности 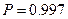 :
:  , тогда
, тогда  кГц.
кГц.
Следовательно, для вероятности  :
:
 кГц.
кГц.
Задача 1.9.
Среднеквадратическое отклонение результатов наблюдений  величины
величины  равно
равно  кГц
кГц
при нормальном законе распределения отклонений.
Какое минимальное число наблюдений – n надо провести, чтобы интервал случайной погрешности результата измерения  был
был  кГц с доверительной вероятностью
кГц с доверительной вероятностью  ?
?
Решение:
Запишем выражение для определения интервала случайных погрешностей:

Отсюда получим соотношение:

Получим 
При  33
33

Отсюда следует, что минимальное число наблюдений равно: 
1.10а) При измерении двух частот получены следующие результаты:


Здесь ±D, Р – соответственно границы интервалов случайных погрешностей и их доверительные вероятности. Определить, какой результат более точный и почему (считать, что случайные погрешности распределены по нормальному закону).
Решение

Пусть s = 1

 , значит доверительные вероятности измерены на разных интервалах. Первая на интервале (-s;s), а вторая (-3s; 3s).
, значит доверительные вероятности измерены на разных интервалах. Первая на интервале (-s;s), а вторая (-3s; 3s).
Для сравнения погрешностей возьмем их на одинаковых интервалах
 значит F2 измерено точнее.
значит F2 измерено точнее.
Задача 1.10а
Решение:
Для определенности количество наблюдений примем равным 100. По исходным данным можно найти СКО:

|

|

|

|

|

|
| пусть |

|
По таблице находим

|

|
Тогда

|

|

|

|

|

|
Как видно, во втором случае СКО меньше, значит и результат точнее
1.12б) Получены следующие результаты измерений величены X:



Запишите эти результаты в соответствии с рекомендациями Государственного стандарта
«Представление результатов измерений».
Решение
1) X = 857,07 кГц; D = ±0,13 кГц; Р = 0,95
2) X = 0,37510 кГц; D = ±0,00101 кГц; Р = 0,9
3) X = 151,01 кГц; D = ±1,28 кГц; Р = 0,997
Задача 1.15
Сопротивление  составлено из двух резисторов с
составлено из двух резисторов с 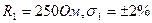 и
и  .
.
1) Чему равно  и интервал его абсолютной погрешности
и интервал его абсолютной погрешности 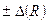 при параллельном включении резисторов.
при параллельном включении резисторов.
2) Чему равно  и интервал его абсолютной погрешности
и интервал его абсолютной погрешности 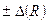 при последовательном включении этих же резисторов.
при последовательном включении этих же резисторов.
Решение:
1.  ;
;  - абсолютная погрешность сопротивления первого резистора;
- абсолютная погрешность сопротивления первого резистора;
2.  ;
;  - абсолютная погрешность сопротивления второго резистора;
- абсолютная погрешность сопротивления второго резистора;
При параллельном включении:
 Ом
Ом

Ответ:  Ом,
Ом, 
При последовательном включении:
 Ом
Ом

Ответ:  Ом,
Ом, 
2.1в Электрическая схема устройства сведена к эквивалентной (рисунок 1), состоящей из последовательно включенных: источника переменного напряжения с частотой  МГц, сопротивлений
МГц, сопротивлений  кОм и
кОм и  кОм.
кОм.
|
|
|
Для измерения падения напряжения  на
на  к нему через кабель подключен вольтметр В3-38 с рабочим диапазоном частот от 20Гц до 7МГц, входным сопротивлением 4МОм, входной емкостью
к нему через кабель подключен вольтметр В3-38 с рабочим диапазоном частот от 20Гц до 7МГц, входным сопротивлением 4МОм, входной емкостью  пФ, емкость кабеля
пФ, емкость кабеля  пФ.
пФ.
 С какой погрешностью
С какой погрешностью  покажет вольтметр значение
покажет вольтметр значение  .
.
Рисунок 1 - Эквивалентная схема устройства.
Решение:
 ;
;
 ;
;
Найдем напряжение на сопротивлении  (сопротивлением
(сопротивлением  пренебрегаем, т.к. его номинал велик):
пренебрегаем, т.к. его номинал велик):  ;
;
 ;
;

Задача 2.4
Вольтметр магнитоэлектрической системы имеет класс точности 0,2, пределы измерения от 0 до 300 В. В каком интервале будут находиться абсолютная  и относительная
и относительная  погрешности измерения 20 и 200 В, когда точность будет выше?
погрешности измерения 20 и 200 В, когда точность будет выше?
Решение:
Магнитоэлектрические приборы – это приборы, в которых ток пропускается через обмотку легкой подвижной катушки (так называемой рамки) расположенной в поле постоянных магнитов. Между током в рамке и полем возникают силы взаимодействия, пропорциональные току, которые поворачивают рамку. Направления действия сил поля сильно зависят от направления входного тока, поэтому для данных типов приборов необходимо соблюдать полярность. Данный тип прибора не предназначен для измерения переменного тока, так как рамка с током будет крутиться все время в разные стороны. Поэтому на входе таких приборов для измерения переменного тока ставят выпрямители для измерения переменного тока.
Известно, что класс точности прибора 0,2, тогда можно написать:
 (1)
(1)
 (2)
(2)
для 20 В:
 - абсолютная ошибка измерения.
- абсолютная ошибка измерения.
 - относительная ошибка измерения
- относительная ошибка измерения
для 200 В:
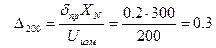
 - абсолютная ошибка измерения
- абсолютная ошибка измерения
 - относительная ошибка измерения
- относительная ошибка измерения
Точность измерения увеличивается при стремлении измеряемого значения напряжения к предельному (это видно из полученных результатов). Таким образом, точность выше при значении измеряемого напряжения 200 В.
Ответ:  ,B
,B

 ,%
,% 
Задача 2.6а
Имеется магнитоэлектрический механизм преобразования с внутренним сопротивлением  , током максимального отклонения
, током максимального отклонения  , классом точности 0.2.
, классом точности 0.2.
Рассчитайте значение добавочного сопротивления  для создания вольтметра на
для создания вольтметра на  , его входное сопротивление и класс точности, если интервал относительной погрешности добавочного сопротивления
, его входное сопротивление и класс точности, если интервал относительной погрешности добавочного сопротивления  .
.
Решение:
По определению класс точности равен  . Отсюда
. Отсюда  . По закону Ома
. По закону Ома 
Теперь можем найти добавочное сопротивление 
Входное сопротивление будет равно

При введении добавочного сопротивления получим новую абсолютную погрешность максимального тока
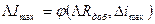
Из определения относительной погрешности можем получить абсолютную погрешность добавочного сопротивления



Рассчитаем класс точности полученного вольтметра

Задача 2.6 а.
Имеется магнитоэлектрический механизм преобразования с внутренним сопротивлением
 Ом, током максимального отклонения
Ом, током максимального отклонения  мА, классом точности 0.2.
мА, классом точности 0.2.
Рассчитайте значение добавочного сопротивления  для создания вольтметра на
для создания вольтметра на
 В, его входное сопротивление и класс точности, если интервал относительной
В, его входное сопротивление и класс точности, если интервал относительной
погрешности добавочного сопротивления  %.
%.
Решение:
Найдем напряжение магнитоэлектрического механизма преобразования:
 В
В
Рассчитаем значение добавочного сопротивления:
 Ом.
Ом.
Рассчитаем входное сопротивление вольтметра:
 Ом
Ом
Рассчитаем класс точности вольтметра:
Для этого рассчитаем абсолютную погрешность вольтметра:
1. Абсолютная погрешность добавочного сопротивления:
 Ом
Ом
2. Абсолютная погрешность напряжения механизма преобразования:
 - класс точности механизма преобразования.
- класс точности механизма преобразования.
 В
В
Запишем уравнение для максимального значения напряжения вольтметра и найдем производные:

3. 

 В
В
Найдем класс точности вольтметра:

Задача 2.6 б
Имеетсяя магнитоэлектрический механизм преобразования с внутренним сопротивлением  Ом, током максимального отклонения
Ом, током максимального отклонения  мА, классом точности
мА, классом точности  .
.
Рассчитайте значение добавочного сопротивления  для создания вольтметра на
для создания вольтметра на  В, его входное сопротивление и класс точности, если интервал относительной погрешности добавочного сопротивления
В, его входное сопротивление и класс точности, если интервал относительной погрешности добавочного сопротивления  .
.
Решение:
При первоначальных условиях вольтметр мог измерять напряжения до  мВ, тогда абсолютная погрешность измерений:
мВ, тогда абсолютная погрешность измерений:  мкВ.
мкВ.
Для увеличения напряжения, которое вольтметр способен измерить вводится дополнительное сопротивление, включенное последовательно с внутренним сопротивлением вольтметра. При том же значении  мА на вольтметре должно падать напряжение
мА на вольтметре должно падать напряжение  В, следовательно входное сопротивление вольтметра должно быть
В, следовательно входное сопротивление вольтметра должно быть  Ом. Отсюда
Ом. Отсюда  Ом.
Ом.  Ом.
Ом.
Выразим зависимость напряжения, падающего на вольтметре, от показаний исходного вольтметра и добавочного сопротивления.
 В.
В.
Найдем частные производные:
 А
А

Абсолютная погрешность получившегося вольтметра.
 В
В
Класс точности получившегося вольтметра.

Задача № 2.9.
Вольтметрами магнитоэлектрической, электромагнитной и электростатической систем измеряется напряжение
 .
.
Что покажет каждый вольтметр, с какой абсолютной погрешностью  , если классы точности каждого
, если классы точности каждого  , пределы измерения от
, пределы измерения от  до
до  В?
В?
· Рассчет показаний вольтметров.
Вольтметр магнитоэлектрической системы покажет  , т.к. может измерять только постоянное напряжение. Вольтметры же двух других систем (электромагнитной и электростатической) измеряют действующее значение и дадут следующее показание:
, т.к. может измерять только постоянное напряжение. Вольтметры же двух других систем (электромагнитной и электростатической) измеряют действующее значение и дадут следующее показание:
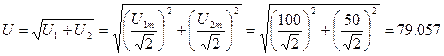 В.
В.
· Рассчет абсолютной погрешности  .
.
 , где
, где  % – класс точности прибора,
% – класс точности прибора,  В – предел измерения. Тогда получаем, что
В – предел измерения. Тогда получаем, что  В.
В.
Задача 3.5 а.
Универсальный осциллограф имеет полосу пропускания частот канала YП от 50 Гц до 50 МГц. Оцените, с какими абсолютной  и относительной
и относительной  погрешностями будут наблюдаться длительности переднего и заднего фронтов импульса, если истинное значение их
погрешностями будут наблюдаться длительности переднего и заднего фронтов импульса, если истинное значение их  мкс.
мкс.
Решение:
Найдем время нарастания:
 нс
нс
Найдем измеренное значение длительности переднего и заднего фронтов импульса:
 нс
нс
Абсолютная погрешность длительности фронтов импульса:
 нс
нс
Относительная погрешность длительности фронтов импульса:

3.6б какой минимальной верхней частотой Fmin полосы пропускания канала Y должен обладать осцилограф для измерения длительности фронта импульса порядка  мкс с погрешностью
мкс с погрешностью  %?
%?
Решение:

 МГц
МГц

 МГц
МГц

 МГц
МГц
 МГц
МГц
Ответ:  МГц
МГц
Задача № 3.13.
Требуется с помощью анализатора спектра (АС) наблюдать спектр частотно-модулированного сигнала


