 |
Cоставление баланса мощности для цепи.
|
|
|
|
Cхема анализируемой цепи

 a
a
 |
b
| R1=8 Ом | R2=10 Ом | R3=2 Ом | R4=4 Ом | R5=6 Ом | E1=20 В | E2=10 В |
Содержание задания
1. Выполнить анализ цепи.
2. Написать систему уравнений Кирхгофа для цепи.
3. Получить главный определитель системы уравнений.
4. Рассчитать цепь (найти токи в ветвях) методом двух узлов.
5. Составить баланс мощности для цепи.
Выполнение анализа цепи.
Анализ цепи показывает, что в ней присутствуют два источника ЭДС и 5 потребителей. Cхема содержит два узла (a, b), 3 независимых контура и 4 ветви. Направления токов в ветвях цепи выбраны произвольно (как показано на схеме). Число ветвей совпадает с числом токов в цепи.
Cоставление системы уравнений по законам Кирхгофа.
Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю. Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только (n – 1) уравнений являются независимыми друг от друга. Cоответственно, по первому закону Кирхгофа составим уравнения в количестве на одно меньшее (n - 1), чем число узлов в цепи, то есть одно уравнение (при этом учитываем, что алгебраическая сумма токов равна нулю):
I1 - I2 - I3 - I4 = 0
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре. Произвольно выбрав направления обходов контуров, по второму закону Кирхгофа составим уравнения для всех независимых контуров цепи, то есть три уравнения, при этом учитывая знаки ЭДС. Запишем данные уравнения вместе с уравнением, составленным по первому закону Кирхгофа, в виде системы:
|
|
|
I1 - I2 - I3 - I4 = 0
I1R1 + I2R2 = E1
-I2R2 + I3R3 = E2
-I3R3 + I4(R4 + R5) = -E2
Получение главного определителя системы уравнений.



 Главный определитель данной системы уравнений строится в соответствии с матрицей системы: в первой строке находятся единицы со знаками “+” и “-“ (в соответствии с первым уравнением), a в других строках – значения сопротивления, написанные в столбце соответствующего тока. При этом учитываются знаки. В случае отсутствия каких-либо значений на их места в определителе ставятся нули. Для системы, указанной выше, главный определитель выглядит следующим образом:
Главный определитель данной системы уравнений строится в соответствии с матрицей системы: в первой строке находятся единицы со знаками “+” и “-“ (в соответствии с первым уравнением), a в других строках – значения сопротивления, написанные в столбце соответствующего тока. При этом учитываются знаки. В случае отсутствия каких-либо значений на их места в определителе ставятся нули. Для системы, указанной выше, главный определитель выглядит следующим образом:







 1 -1 -1 -1 1 -1 -1 -1
1 -1 -1 -1 1 -1 -1 -1




 R1 R2 0 0 8 10 0 0 ___ 10 0 0 8 0 0 8 10 0 8 10 0
R1 R2 0 0 8 10 0 0 ___ 10 0 0 8 0 0 8 10 0 8 10 0



 0 -R2 R3 0 0 -10 2 0 -10 2 0 0 2 0 0 -10 0 0 -10 2
0 -R2 R3 0 0 -10 2 0 -10 2 0 0 2 0 0 -10 0 0 -10 2
0 0 -R3 (R4 + R5) 0 0 -2 10 0 -2 10 0 -2 10 0 0 10 0 0 -2

 10*20 + 8*20 - 8*(-100) + 8*20 = 1320
10*20 + 8*20 - 8*(-100) + 8*20 = 1320
Расчет цепи (нахождение токов в ветвях) методом двух узлов.
Формула для расчета напряжения между двумя узлами выглядит так: 
В соответствии с ней рассчитаем напряжение между узлами:








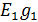 –
–  20*0.125 - 10*0.5
20*0.125 - 10*0.5
 +
+  +
+  +
+  0.125 + 0.1 + 0.5 + 0.1
0.125 + 0.1 + 0.5 + 0.1
где проводимости ( = 1/ Rn
= 1/ Rn  = 1 /(R4 +R5)) ветвей равны:
= 1 /(R4 +R5)) ветвей равны:
 = 1 / R1 = 1 / 8 = 0.125 Cм
= 1 / R1 = 1 / 8 = 0.125 Cм
 = 1 / R2 = 1 / 10 = 0.1 Cм
= 1 / R2 = 1 / 10 = 0.1 Cм
 = 1 / R3 = 1 / 2 = 0.5 Cм
= 1 / R3 = 1 / 2 = 0.5 Cм
 = 1 / (R4 + R5) = 1/(4+6) = 0.1 Cм
= 1 / (R4 + R5) = 1/(4+6) = 0.1 Cм
Рассчитаем токи, используя обобщенный закон Ома:
I1 = ( –
–  )*
)*  = (20 - (-3.03)) * 0.125 = 2.789 A
= (20 - (-3.03)) * 0.125 = 2.789 A
I2 =  *
*  = (-3.03) * 0.1 = -0.303 A
= (-3.03) * 0.1 = -0.303 A
I3 = ( +
+  )*
)*  = (10 - 3.03) * 0.5 = 3.485 A
= (10 - 3.03) * 0.5 = 3.485 A
I4 =  *
*  = (-3.03) * 0.1 = -0.303 A
= (-3.03) * 0.1 = -0.303 A
Знак “-“, полученный при расчете токов I2 и I4, говорит о том, что истинные направления токов противоположны показанным на схеме.
Данные токи могут быть также найдены с помощью главного определителя и формул Крамера, для чего необходимо решить систему уравнений Кирхгофа.
В соответствии с формулами и правилами вычислений:
I1 = Δ1/Δ
I2 = Δ2/Δ
I3 = Δ3/Δ
I4 = Δ4/Δ
Определители Δn получаются путем внесения правого столбца значений cистемы (0, E1, E2,-E2, т.e. 0, 20, 10, -10) вместо соответствующего n-го столбца.
|
|
|
Они равны(подробности вычислений опущены):
| Δ1 = |
| = 3800 | ||||||||||||||||||||||||||||||||||||
| Δ2 = |
| = -400 |
| Δ3 = |
| = 4600 | |||||||||||||||||||||||||||||||||||
| Δ4 = |
| = -400 |
Вычисляем токи, учитывая знаки получившихся определителей:
I1 = Δ1/Δ = 3800 / 1320 = 2.87878… ≈ 2.879
I2 = Δ2/Δ = (-400) / 1320 = - 0.30303… ≈ -0.303
I3 = Δ3/Δ = 4600 / 1320 = 3.484848… ≈ 3.485
I4 = Δ4/Δ = (-400) / 1320 = - 0.30303… ≈ -0.303
Таким образом, вычисления выполнены верно.
Подставим получившиеся токи в уравнение, cоставленное по первому закону Кирхгофа:
I1 - I2 - I3 - I4 = 2.879 – (-0.303) - 3.485 - (-0.303) = 0
Соответственно, расчет токов выполнен верно.
Cоставление баланса мощности для цепи.
Баланс мощностей для цепи: если баланс выполняется, то мощность источников (источника) должна быть равна мощности потребителей (Pист. = Pпотр.), где Pпотр. = UI = I2R, Pист. = EI (в соответствии со схемой). Выполняем проверку:
Pист. = E1I1 + E2I3 = 20*2.879 + 10*3.485 = 92.43 Вт
Pпотр. = =(I1)2R1+(I2)2R2+(I3)2R3+(I4)2(R4+R5) = 2.879*2.879*8+(-0.303)*(-0.303)*10+3.485*3.485*2+(-0.303)*(-0.303)(4+6) = 92.435758 ≈ 92.43 Вт
Pист.≈ Pпотр. Таким образом, баланс мощностей выполняется.
|
|
|




