34. Аналитический метод определения давления грунта на подпорную стену.

Такой метод определения давления грунта применяется в простейших случаях при горизонтальной поверхности грунта и вертикальной задней грани подпорной стенки, при с = 0 и действии равномерно распределенной нагрузки по поверхности призмы обрушения.

Определение давления идеально сыпучего грунта (с = 0) на вертикальную абсолютно гладкую подпорную стенку при горизонтальной засыпке. Рассмотрим условие предельного равно­весия элементарной призмы, вырезанной из призмы обрушения вблизи задней грани подпорной стенки (рис. 8. 13, а).

 На гори­зонтальную и вертикальную площадки этой призмы при трении о стенку, равном нулю, будут действовать главные напряжения s1 (большее) и s3 (меньшее). При небольших горизонтальных смещениях стенки возникнет предельное равновесие рассматри­ваемой элементарной призмы. Соотношение между ними  бу­дет обусловлено уравнением (8. 1). На глубине z  величина s1 = yz. Отсюда

s3 = yz tg² (45° — ф/2). (8. 17)

Так как s3 прямо пропорционально глубине z, а остальные величины для однородного грунта постоянны, эпюра давления грунта на подпорную стенку будет треугольной (рис. 8. 13, а). Площадь этой эпюры соответствует равнодействующей активно­го давления грунта Еa на подпорную стенку:

Еa=samax H/2

Подставив в выражение для Ea значение s3max по уравне­нию (8. 17) с учетом, что в таком случае z = Н, получим

Еa= (уH²/2) tg² (45° - ф/2).         (8. 18)

Точка приложения равнодействующей Еa находится в центре тяжести эпюры давления s3.

Аналогично, исходя из выражения  (8. 7), найдем значение пассивного отпора грунта. В этом случае в условиях предельного равновесия горизонтальное напряжение s1 больше вертикально­го s3. Равнодействующая пассивного отпора при заглублении на величну H конструкции, передающей давление иа грунт, со­ставит: Е_р =» (уH²/2) tg² (45° + ф/2).      (8. 18)

Пользоваться выражением  (8. 18) надо с большой осторожностью, так как расхождение с точным решением теории предельного равновесия значительно. Полученные величины Е_а и Е_р имеют некоторый запас, по­скольку при их определении не учтено трение грунта о подпор­ную стенку, развивающееся при смещении призм обрушения и выпирания. Для сокращения записи часто обозначают

tg² (45° - ф/2) = la; tg² (45° + ф/2) = lp(8. 19)

la  и  lp называют коэффициентами соответственно активного и пассивного давления. Следует помнить, что горизонтальное давление на ограждаю­щую конструкцию может принимать различные значения — от ак­тивного давления до пассивного отпора. Это давление зависит, в частности, от направления и величины смещений ограждаю­щей конструкции. При отсутствии смещений давление на конст­рукцию, находясь в указанных пределах, будет зависеть от предыстории загружения грунта.

Учет равномерно распределенной нагрузки, приложенной к поверхности грунта.

Пусть к поверхности грунта приложена равномерно распределенная нагрузка q (рис. 8. 13, 6). Действие этой нагрузки молено заменить действием слоя грунта толщиной h = q/y. Продолжим мысленно подпорную стенку на высоту Н и получим точку, В1. Тогда будет справедливо выражение (8. 17), если считать глубину z от верха фиктивной подпорной стенки. Найдем значения аз на глубинах h и Н + h:

s3=Vh tg² (⁴⁵° — ф/2);

s3max = V(H+h) tg² (45° — ф/2) (8. 20)

По этим значениям построим эпюру активного давления на подпорную стенку и определим суммарное активное давление Еa, как площадь трапеции с основанием АВ:

Еa= (s3'+s3max)/2 H= V/2(H²+2Hh) tg² (45° — ф/2) (a) Верхняя треугольная часть эпюры не создает давления на стен­ку. Сила Еa приложена в центре тяжести эпюры s3. Определение давления связного грунта (ф не равно0, с не равно0) на вертикальную абсолютно гладкую подпорную стенку при го­ризонтальной засыпке. Заменим по формуле (2. 23) сцепление действием всесторонних сил связности р_е = с ctgф, которые приложим к поверхности грунта и по контакту грунт — подпор­ная стенка (рис. 8. 13, б). Теперь составим выражение для s3 на глубине z. Согласно равенству (8. 20), учитывая силы связ­ности Ре, получим

s3 = V (z + h) tg² (45° - ф/2)-p_e. (б)

подставим в выражение (б) значения h = р_е/V и ре — = c-ctg ф. Тогда

s3 = V[ z + (с ctgф/V] ]tg² (45— ф/2) — с • ctg ф

Отсюда путем тригонометрических преобразований получим

s3  = Vz tg² (45° — ф/2) — 2с • tg (45° — ф/2). (8. 21)

Сопоставляя (8. 21) с (8. 17), отметим, что первое слагаемое в (8. 21) характеризует давление сыпучего грунта без учета сцепления, а второе показывает, насколько снижается интенсив­ность давления вследствие того, что грунт обладает сцеплением. Следовательно, это выражение можно представить в виде: Ста = Офз — (Уса,            (8. 22)

гдеs3 =sф3-sс3

sф3  = Vz tg² (45° — ф/2)

s_Сз = 2с • tg (45° — ф/2).

Для определения суммарного активного давления целесооб­разно построить треугольную эпюру давления s_ф3, приняв z=H  и прямоугольную эпюру давления интенсивностью s_ф3. Геометрическим суммированием (наложением) получим эпюру активного давления на подпорную стенку в виде заштрихован­ного треугольника (см. рис. 8. 13, в). В верхней части стенки грунт теоретически не давит, а удерживает подпорную стенку. Однако обеспечить сцепление между подпорной стенкой и грун­том трудно, поэтому считают, что на участке h_c стенка не испы­тывает давления грунта. Когда известна эпюра давления, на­хождение величины Еa и точки приложения не представляет трудностей. Выше были рассмотрены простейшие случаи определения ак­тивного давления грунта на подпорные стенки. При наклонном положении задней грани подпорной стенки и наклонной поверх­ности засыпки за ней интенсивность активного давления и его суммарная величина могут быть определены для сыпучего грун­та по справочникам или методом, изложенным ниже. При этом значение ог_с3 находят по формуле

s_Сз= С*COS ф/cos² [45° — (ф + b)/2]            

где (b — угол между вертикалью и задней гранью подпорной стенки; значе­ние р положительно, когда грунт нависает над задней, гранью подпорной стенки, и отрицательно, если стенка наваливается на грунт.

Направление Еa при отсутствии трения грунта о подпорную стенку принимается горизонтальным при отрицательном значе­нии b и перпендикулярным к задней грани при b  0.

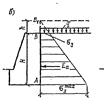
Схема для определения давления грунта на глад. подпорную стенку

а-идеально сыпучего, б-то же, с учетом распред. нагрузки, в- обладающего сцеплением

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: