 |
Конструирование коэффициентов передаточной функции
|
|
|
|
Наиболее важный результат в области формализации процедур поиска принципиальных схем, очевидно, связан с появлением в 1970 г. работы S. Mitra и M. Soderstrand [5], где предложено сопоставление принципов конструирования коэффициентов передаточной функции. И несмотря на то, что при таком подходе перебор вариантов сохраняется, он осуществляется на более раннем этапе и не связан с анализом принципиальных схем. Эта же задача – отсечение заведомо бесполезных структур – рассматривалась также Б.И. Блажкевичем [6]. Содержательная сторона настоящего подхода заключается в следующем.
Любая линейная активная схема в соответствии с утверждением И. Сандберга [9] может быть представлена векторным сигнальным графом (рис. 3).
В этом случае ее передаточная функция определяется следующим соотношением:
, (16)
где Т – вектор-строка (1N), каждый элемент которого является коэффициентом передачи пассивной части схемы с выхода активного элемента к выходу схемы (y0);
А – вектор-столбец (N1), каждый элемент которой является передачей пассивной части схемы с входа (Х0) ко входу активного элемента;
ВТ– матрица (NN), каждый элемент которой представляет собой передачу пассивной части схемы с выхода i-го активного элемента ко входу j-го активного элемента;
{K(p)} – диагональная матрица (NN), элементы которой являются передаточными функциями активных элементов;
N – число активных элементов схемы; t0 – передаточная функция (сквозная передача) схемы при отсутствии активных элементов.
Рис. 3. Векторный сигнальный граф многоконтурной электронной схемы
В этом случае ее передаточная функция определяется следующим соотношением:
, (16)
где Т – вектор-строка (1N), каждый элемент которого является коэффициентом передачи пассивной части схемы с выхода активного элемента к выходу схемы (y0);
|
|
|
А – вектор-столбец (N1), каждый элемент которой является передачей пассивной части схемы с входа (Х0) ко входу активного элемента;
ВТ– матрица (NN), каждый элемент которой представляет собой передачу пассивной части схемы с выхода i-го активного элемента ко входу j-го активного элемента;
{K(p)} – диагональная матрица (NN), элементы которой являются передаточными функциями активных элементов; N – число активных элементов схемы; t0 – передаточная функция (сквозная передача) схемы при отсутствии активных элементов.
Учитывая, что любая передаточная функция может быть представлена отношением двух полиномов
, (17)
устанавливается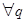 
однозначная связь
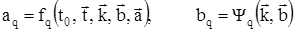(18)
где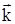 
– вектор коэффициентов передачи активных элементов; 
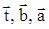– векторы компонентов Т, В, А.
Таким образом, процедура проектирования сводится к анализу способов конструирования коэффициентов (18) и выбору предпочтительного варианта реализации схемы.
Важным следствием такого подхода является возможность декомпозиции задачи на ряд составляющих.
Во-первых, многообразие функциональных зависимостей компонент векторов А, Т и матрицы В от структуры и параметров пассивной части схемы позволяет осуществить поэтапный отбор желаемых способов реализации коэффициентов (18), а также независимо зафиксировать их отдельные составляющие и, следовательно, оперировать локальными частотно-зависимыми передачами. Так, представив (16) в форме Мэзона
(19)
можно перейти при синтезе схемы к выбору простейших решающих усилителей. Именно это позволило автору в 70-е гг. получить более 10-ти новых низкочувствительных принципиальных схем устройств частотной селекции.
Во-вторых, с учетом инерционных свойств активных элементов, матрица К может быть представлена в следующем виде:
|
|
|
, (20)
где Ki, Пi – статический коэффициент передачи и площадь усиления i-го активного элемента. Это позволяет расширить систему (17):
(21)
и, следовательно, учесть в процессе выбора предпочтительных способов конструирования коэффициентов передаточной функции влияние площади усиления активных элементов на любые параметры проектируемой системы. Указанный подход позволил обосновать двухканальные цепи, обладающие свойством взаимной компенсации влияния отдельных активных элементов на параметры звеньев второго порядка, и выявить существующие ограничения на этот уровень [10].
Однако, несмотря на возможность детализации, решение практических задач существенно осложняется большим числом изоморфных схем. Так, при синтезе низкочувствительных цепей, когда используется декомпозиция компонентов матрицы В функцией первого порядка
(22)
знаменатель (16) согласно процедуре Бине-Коши будет иметь вид:
, (23)
где Mi-B – i-й главный минор аддитивно обратной матрицы В.
В классе канонических схем второго порядка с двумя активными элементами необходимо выполнить логические и арифметические условия
(24)
и
(25)
которые приводят к четырем изоморфным схемам.
Первая группа изоморфных схем соответствует изменению индексов активных элементов, а вторая – конкретному виду функции (22) (индексы i и j меняются местами). В общем случае количество таких схем может быть определено через следующее соотношение:
структурный синтез генетический автоматизированный процедура
(26)
Как показывает опыт решения практических задач, именно изоморфизм затрудняет построение новых структур. Особенно это проявляется при их автоматизированном поиске.
Одним из возможных выходов из сложившегося положения является разложение функции (16) в форме (19) по виду характеристических полиномов решающих усилителей, которая совместно со структурой вектора Т позволяет осуществлять разветвление процедуры синтеза. Например, для звеньев второго порядка общий для числителя и знаменателя (19) полином будет иметь 6 вариантов своего формирования [5]:
(27)
Каждому из полученных разложений для конкретного числа активных элементов будут соответствовать только две принципиальные схемы, и, следовательно, при большом N существенно сократится перебор вариантов.
|
|
|
Так, для второго варианта разложения после формальных преобразований получим сигнальный граф, изображенный на рис. 4.
Рис. 4. Сигнальный граф схемы варианта 2
Таким образом, из рассмотрения исключены варианты, связанные с заменой индексов 1«2, 3«2, что и позволило получить единственную принципиальную схему. Анализ полученного решения показал значительно более низкое влияние частотных свойств активных элементов на ее параметры по сравнению с ранее известными схемами.
Приведенный подход позволяет, в частности, еще более сузить область поиска желаемых структур. Например, при построении звеньев второго порядка с действительными нулями коэффициента передачи, когда по соображениям чувствительности целесообразно отказаться от разностного принципа формирования затухания нуля передаточной функции, можно выделить специальный двухканальный тип частотозависимой цепи со вторым, четвертым и пятым вариантами разложения функции (7).
|
|
|
