 |
сделать схематический чертеж.
|
|
|
|
СПИСОК ЛИТЕРАТУРЫ
1. Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов:в 3т.-5-е изд.,стер.-М.:Дрофа.- (Высшее образование. Современный учебник).т.2. Дифференциальное и интегральное исчисление.-2003.-509 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс.Т.1. -2001.- 415 с.
3. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. – 8-е изд.-М.: Физматлит. т.1 – 2001. -697 с.
4. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. -22-е изд., перераб.- СПб: Профессия, 2003.-432 с.
5. Кудрявцев Л.Д. Курс математического анализа. Учеб. для вузов: В 3-х томах. – 5-е изд., перераб. и доп. –М.: Дрофа. Т.1. – 2003.-703 с.
6. Ильин В.А., Позняк Э.Г. Основы математического анализа. Учеб. для вузов в 2-х частях. – 6-е изд. стер. –М. Физматлит, 2002, -646 с.
7. Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я.-6-е изд..-М.: ОНИКС 21 век, ч.2. -2002.-416 с.
Решение типового варианта контрольной работы.
1. Вычислить пределы функций.
а) Найти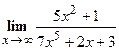 
.
Решение. Прежде всего, проверим, применимы ли к данной дроби теоремы о пределах, или мы имеем дело с неопределенностью. Для этого найдем пределы числителя и знаменателя дроби. Функции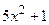 
и 
являются бесконечно большими. Поэтому,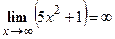 
, 
.
Следовательно, имеем дело с неопределенностью вида 
.
Для раскрытия этой неопределенности и использовании теоремы о пределе отношения двух функций выделим в числителе и в знаменателе 
в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.
Ответ. 0.
б) Найти 
.
Решение. Для раскрытия неопределенности 
в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.
|
|
|
Ответ. -9.
Найти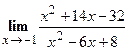 
.
Решение. Для вычисления данного предела подставим значение 
в функцию, стоящую под знаком предела. Получим,
.
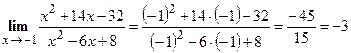Ответ. -3.
в) Найти 
.
Решение. Для раскрытия неопределенности в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.
Ответ. 
.
г) Найти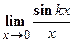 
.
Решение. Для раскрытия неопределенности в этом случае, нужно выделить первый замечательный предел: 
Ответ. k
д) Найти 
.
Решение. Для раскрытия неопределенности 
в этом случае, нужно произведение преобразовать в частное, то есть неопределенность свести к неопределенности или 
.
Выделяем первый замечательный предел, то есть, умножаем числитель и знаменатель на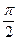 
. Получаем,
.
Ответ.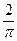 
.
е) Найти 
.
Решение. Для раскрытия неопределенности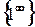 
в этом случае, нужно выделить второй замечательный предел: 
.
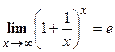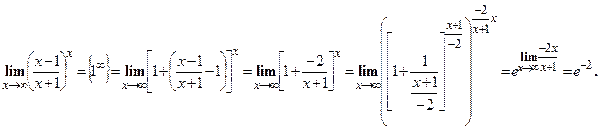
Ответ. 
.
ж) Найти 
Решение. Для раскрытия неопределенности 
в этом случае, нужно выделить второй замечательный предел: 
.
Ответ. 
.
Найти 
Решение. Подставим значение 
в функцию, стоящую под знаком предела. Получим,
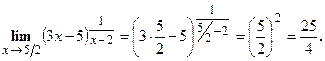
Ответ. 
.
2. Задана функция 
и два значения аргумента 
.
Требуется:
- найти пределы функции при приближении к каждому из данных значений 
слева и справа;
- установить является ли данная функция непрерывной или разрывной для каждого из данных значений ;
- сделать схематический чертеж.
Решение. Найдем левый и правый пределы в точке 
.
Левый предел конечен и равен 0, а правый предел бесконечен. Следовательно, по определению точка разрыва второго рода.
Найдем левый и правый пределы в точке 
.
, т.е. точка непрерывности функции .
Сделаем схематический чертеж.
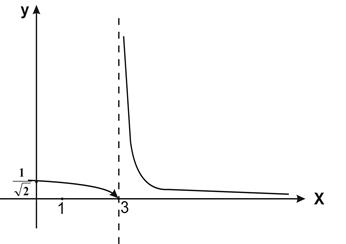
Рис. 1
3. Функция задается различными аналитическими выражениями для различных областей независимой переменной.
|
|
|
Требуется:
1) найти точки разрыва функции, если они существуют;
2) найти скачок функции в каждой точке разрыва;
сделать схематический чертеж.
Решение. Функция 
непрерывна для 
, функция 
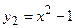непрерывна в каждой точке из 
, функция 
непрерывна в каждой точке интервала 
.
Точки, в которых функция может иметь разрыв, это точки 
и 
, где функция меняет свое аналитическое выражение.
Исследуем точку .
, 
, 
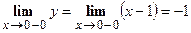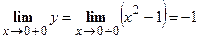. Таким образом, точка 
есть точка непрерывности функции 
.
Исследуем точку 
.
, 
, 
. Таким образом, односторонние пределы существуют, конечны, но не равны между собой. По определению, исследуемая точка – точка разрыва первого рода. Величина скачка функции в точке разрыва равен 
.
Сделаем схематический чертеж
Рис. 2
Контрольная работа №4.
Вариант 1
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
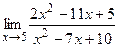в) 
;
г) 
;
д) 
;
е) 
; 
.
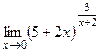2. Дана функция 
и два значения аргумента 
.
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек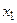 
и 
.
, 
.
3. Для кусочно-заданной функции 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 2
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция 
и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 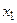и .
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 3
1. Вычислить пределы функций.
а) 
б) 
; 
;
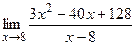в) 
;
г) 
;
д)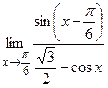 
;
е) 
; 
.
2. Дана функция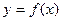 
и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
|
|
|
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 
и 
.
, 
.
3. Для кусочно-заданной функции 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 4
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г)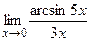 
;
д) 
;
е) 
; 
.
2. Дана функция 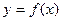и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 5
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
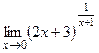2. Дана функция 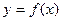и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и 
.
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 6
1. Вычислить пределы функций.
а) 
;
б)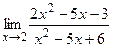 
; 
;
в) 
;
г)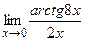 
;
д) 
;
е) 
; 
.
2. Дана функция 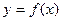и два значения аргумента 
.
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 
и .
, 
.
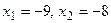3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
|
|
|
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 7
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция 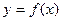и два значения аргумента 
.
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 
и 
.
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
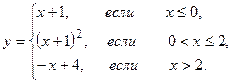
Контрольная работа №4.
Вариант 8
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
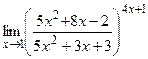2. Дана функция 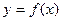и два значения аргумента 
.
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
3. Для кусочно-заданной функции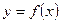 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 9
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция 
и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
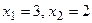3. Для кусочно-заданной функции 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 10
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция 
и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
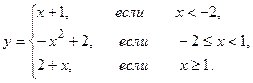
Контрольная работа №4.
Вариант 11
1. Вычислить пределы функций.
|
|
|
а)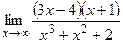 
;
б) 
; 
;
в)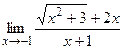 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 12
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г)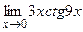 
;
д) 
;
е)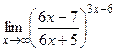 
; 
.
2. Дана функция и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 13
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
г) 
;
д) 
;
е) 
; 
.
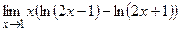2. Дана функция 
и два значения аргумента 
.
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 
и 
.
, 
.
3. Для кусочно-заданной функции 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 14
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
в) 
;
г)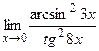 
;
д) 
;
е)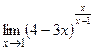 
; 
.
2. Дана функция и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
, 
.
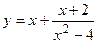3. Для кусочно-заданной функции .
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 15
1. Вычислить пределы функций.
а) 
;
б)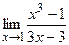 
; 
;
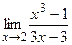в) 
;
г) 
;
д)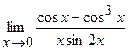 
;
е) 
; 
.
2. Дана функция и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек 
и .
, 
.
3. Для кусочно-заданной функции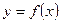 
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 16
1. Вычислить пределы функций.
а) 
;
б) 
; 
;
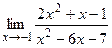в) 
;
г) 
;
д) 
;
е) 
; 
.
2. Дана функция и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений 
;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и 
.
, 
.
3. Для кусочно-заданной функции .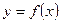
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
Контрольная работа №4.
Вариант 17
1. Вычислить пределы функций.
а)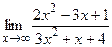 
;
б) 
; 
;
в) 
;
г)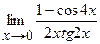 
;
д) 
;
е) 
; 
.
2. Дана функция 
и два значения аргумента .
Требуется.
1)Найти значение функции при стремлении аргумента к каждому из данных значений ;
2) Определить, является ли функция непрерывной или разрывной при данных значениях ;
3) Сделать схематический чертеж в окрестности точек и .
|
|
|
