Оценка влияния емкости полнодоступного пучка на характеристики .

Курсовая работа по курсу теории телетрафика

 

 

Выполнил: студент

 гр. A-91в

                                                          Воропаев В.В.

 

 

Санкт-Петербург

2013

 

 Система М|М| v: Обслуживание простейшего потока полнодоступным пучком из v линий при показательном распределении времени обслуживания и неограниченном числе мест для ожидания.

Вариант 9

 

Практическим применением модели M|M|v является расчёт систем коммутации сообщений и управляющих устройств систем коммутации каналов. В некоторых системах машинных АТС по системе с ожиданием работают устройства разговорного тракта. По системе с ожиданием работают междугородние каналы при ручном обслуживании.

Исходные условия.

 

Для системы М|М|v входными воздействиями являются:

· набор чисел: λ_к =λ, k≥0- постоянная интенсивность поступления вызовов,
β_к- интенсивность освобождения вызовов:

 

· функции:

A(x)=1- e ^-λx

A(x)-функция распределения промежутков между вызовами.

· функции:

H(x)=1- e ^-βx

H(x)-функция распределения длительности обслуживания вызовов.

 

Макромодель системы включает в себя:

· условие устойчивости: λ/β<v;

· алгебраические уравнения вида:

Набор откликов

 

Набор откликов содержит:

· аналитические выражения вероятностей P_i,P_v,W_j:

 

 

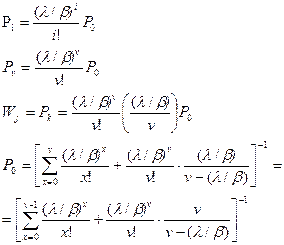
· Вероятность потерь по времени:

· Функция распределения ожидания начала обслуживания:

· Среднее время ожидания начала обслуживания, отнесённое ко всем поступающим вызовам, и среднее время ожидания начала обслуживания, отнесённое к вызовам, попадающим на ожидание:

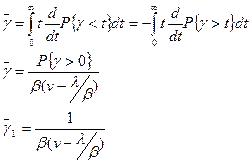
· Средняя длинна очереди:

1. Обработка результатов машинного расчета характеристик системы М|М| v.

Вероятность того, что в системе занято i линий.

Вывод: из графиков видно что, с увеличением i (числа занятых линий) вероятность Pi  уменьшается.

  Вероятность того, что в системе занято v линий и на ожидании j вызовов.

 

 

Вывод: С увеличением i (число вызовов на ожидании) распределение вероятности того, что в системе занято V линий и i находится на ожидании снижается

 

 

Вывод: по графику видно, что при увеличении  , вероятность задержки вызова увеличивается.

 

 

Вывод: по графику видим, что при увеличении  среднее время ожидания начала обслуживания увеличивается.

 

Вывод: с увеличением  средняя длина очереди увеличивается.

2. Оценить качественные изменения характеристик  и j (их улучшение или ухудшение) в диапазоне . Сделать выводы относительно устойчивости функционирования системы при ® V.

 

Вывод: при увеличении  ,  и j увеличивается, то есть система работает хуже.

Вывод: при  ® V характеристики  и j ухудшаются Þ система будет работать нестабильно.

 

 

Оценка влияния емкости полнодоступного пучка на характеристики.

 

Оценить влияние емкости полнодоступного пучка v на характеристики можно при помощи сопоставления моделей М|М|1 и М|M|v в диапазоне 0≤λ/β<1.

Для системы М|М|v:

 

Для системы М|М|1:

Характеристики ,  и  одинаковые, а

 

	Для модели M|M|1	Для модели M|M|V
0.2	0.2	2.358 ×10-14
0.4	0.4	2.018 ×10-11
0.6	0.6	9.728 × 10-10
0.8	0.8	1.445 × 10-8

Видно, что модель M|M|v лучше, чем M|M|1, так как значение

 меньше.

 

 

4. Оценка математического ожидания числа одновременно занятых линий в системе  и математическое ожидания числа свободных линий .

Оценим в диапазоне λ/ β математическое ожидание числа одновременно занятых линий в системе   и математическое ожидание числа свободных линий , где

 

λ/ β
0,4	0,4	9,6
0,8	0,8	9,2
1,6	1,6	8,4

Вывод: при увеличении λ/ β,  увеличивается, а  уменьшается.

 

5. Вывод формулы Литтла для системы М ½ М ½ V ½.

 

k=l T - общая формула Литтла

k - среднее число требований в системе;

l - параметр потока, который характеризует интенсивность поступления вызовов в какой-то момент времени;

Т - среднее время пребывания сообщения в системе коммутации или СРИ:

Т=gз+tобсл

gз - среднее время ожидания обслуживания с системе;

так как система М½М½V - эта система с ожиданием, то

gз=P(γ>0)/(β(υ – λ/ β));

tобсл - среднее время обслуживания вызова в системе приборами;

 

       Таким образом, формула Литтла для системы М½М½V будет следующей:

 

 

6. Оценка влияния функции распределения длительности обслуживания на среднее время ожидания   путем сопоставления моделей M | M | V и M | D | V.

 

Значения  для модели M|D|V возьмем из кривых, построенных по результатам Кроммелина. V= const = 6.

 

При λ/ β = 0,4      =

При λ/ β = 0,8          =

 

 

Значения  для модели M|M|V рассчитаем по формуле:

 

При λ/ β = 0,4        =

При λ/ β = 0,8        =

Поделиться:

Воспользуйтесь поиском по сайту: