Проверка на прочность поперечной балки

Двухстоечного электромеханического подъемника»

Оглавление

1. Устройство и принцип работы винтового электромеханического подъёмника

2. Расчет силовой винтовой передачи

3. Расчет опорных роликов

4. Проверка на прочность поперечной балки

5. Расчет на прочность кронштейна поперечной балки

6. Расчет на прочность сварного шва

7. Определение параметров электродвигателя (мотора-редуктора)

8. Расчет стоимости подъемника

Литература

Устройство и принцип работы винтового электромеханического подъёмника

 

Рассмотрим устройство 2-стоечного напольного подъемника (рис. 1). Он состоит из двух коробчатых стоек и поперечины 2. В каждой стойке размещен винт 3, по которому перемещается грузоподъемная балка 4 с раздвижными подхватами 5. Ходовые винты приводятся во вращение от электродвигателя 6 через редуктор 7, установленный на одной из стоек. Вращение на другой винт передается с помощью цепной передачи 8, смонтированной внутри поперечины 2.

Подъемник крепится к полу анкерными болтами 9. Упорные ролики 10 освобождают винт от изгибающих усилий.

 

Рисунок 1 – Винтовой электромеханический подъемник.

Расчет силовой винтовой передачи

 

Средний диаметр винта и гайки:

 

d₂ = √(Q/π_*k_1*k_2*[q]), (1)

 

где Q – вес, приходящийся на каждую стойку,

k₁ - отношение веса гайки h к среднему диаметру резьбы, принимаем

 

k₁= h/d₂ = 1,6

 

k₂ – коэффициент, зависящий от вида резьбы, для трапецеидальной резьбы k₂ = 0,5

[q] – допускаемое давление для резьбы, [q] = 10 МПа.

С учетом запаса прочности, необходимого для ходового винта подъемника, принимаем трапецеидальную однозаходную правую резьбу с диаметром d₂ = 34мм и шагом h = 3 мм.

Принимаем материал винтовой коры:

для винта – Сталь 45;

для гайки – Бр ОЦС-6-6-3.

Проверяем условие самоторможения винта:

 

L< ρ, (2)

 

где L – угол подъема винтовой линии,

ρ – угол трения, для винтовой пары сталь-бронза ρ = 4º.

 

L = arctg (p/(π _* d_cp ), (3)

 

где р – шаг резьбы, р = 3 мм.

L = arctg (3/(3,14 _* 34)) = 1,6º,

 

так как 1,6º<4º, то условие самоторможения выполняется.

Коэффициент полезного действия винтовой пары

 

η = tg L/tg (L + ρ), (4)

η = tg 1,6/tg (1,6 + 4) = 0,4

 

Выполним проверку винта на прочность с учетом совместного действия деформации сжатия и кручения. Условие прочности:

 

σ_пр < [σ], (5)

 

где σ_пр – приведенное напряжение от действия деформации сжатия и кручения

[σ] – допускаемое напряжение.

 

σ_пр = √(σ_сж²+4τ²), (6)

 

где σ_сж – напряжение сжатия,

τ – касательное напряжение.

 

σ_сж = 4Q/(π _* d₂²), (7)

Q = d_cp²_*π_*k_1*k_2*[q] = 0,034²_*3,14_*1,6_*0,5_*10_*10⁶=22940 кН

σ_сж = 4 _*22940/3,14_*0,034²= 32_*10⁶ Па = 32 МПа,

τ = М_кр/W_р,

 

где М_кр – крутящий момент, прилагаемый к винту,

W_р – полярный момент сопротивления

М_кр = 0,5_*Q_*d₂²_*tg(L+ρ)+М_п , (9)

 

где М_п – момент трения на опорах винта

 

М_п = 0,25_*d_2*Q_*f₀, (10)

 

где f₀ – коэффициент трения в подшипниках, f₀=0,01

 

М_п = 0,25_*0,034_*22940_*0,01 = 2468 Н_*м

М_кр = 0,5_*22940_*0,034²_*tg(1,6+4)+2468 = 2516 Н_*м,

W_p = π_*d_в³/16, (11)

d_в = d₂-H₁-a_c, (12)

 

где Н₁ – высота профиля, Н₁=1,5 мм,

a_с – зазор по вершине резьбы, a_с = 0,25.

 

d_в = 34-1,5-0,25=32,25 мм

Wр = 3,14_*0,03225³/16 = 6,6_*10^-6мм³

τ = 2516/6,6_*10^-6 = 38,1 МПа

σ_пр = √(32²+4*38,1²)=82,6 МПа,

σ_пр = 82,6 МПа < [σ] = 160 МПа,

 

следовательно, условие прочности выполняется.

Далее выполняем проверочный расчет винта на продольный изгиб по внутреннему сечению.

Гибкость стержня

 

λ = μ_*l/τ_min, (13)

 

где μ – коэффициент приведенной длины стержня,

l – длина стержня, l = 1,5м,

τ_min – минимальный радиус инерции рассчитываемого сечения стержня.

 

μ = μ_1*μ_2, (14)

 

где μ₁ – коэффициент, учитывающий способ заделки концов стержня, μ₁= 0,7;

μ₂ – коэффициент, учитывающий изменение формы стержня по длине,

 

μ₂= 1

μ = 0,7_*1=0,7

τ_min = d_min/4, (15)

 

d_min – минимальный диаметр стержня, который равен внутреннему диаметру резьбы, d_min =32,25 мм.

 

τ_min = 32,25/4 = 8,06 мм.

λ = 0,7_*1,5/8,06 = 130

 

Определяем по таблице коэффициент уменьшения допускаемого напряжения при продольном изгибе, при λ =130 для материала Сталь 45 φ=0,33

Допускаемое напряжение при расчете на устойчивость

 

[σ_у] = φ_*[σ], (16)

[σ_у] = 0,33_*160 = 52,8 МПа

 

Запас устойчивости

 

n_у = [σ_у]/σ_сж, (17)

n_у = 52,8/32 = 1,65

 

так как n_у = 1,65 больше требуемого n_у = 1, то запас устойчивости достаточен.

Необходимое число витков резьбы в гайке

 

Z = 4_*Q/(π_*[g]_*(d_н² – d_в²)), (18)

 

где [g] – допускаемое удельное давление в сопряжении винт-гайка, для пары сталь-бронза принимаем [g] = 12 МПа,

d_н – наружный диаметр винта,

d_в – внутренний диаметр винта.

 

Z = 4_*22940/(3,14_*12_*(0,034² – 0,03225²)) = 27

 

Высота гайки

 

h = p_*z = 3*27 = 81 мм

 

Наружный диаметр гайки

 

D_н = √((4_*Q_*k/(π_*[σ_p]))+d_н², (19)

 

где k – коэффициент запаса прочности, k=1,5,

[σ_р] – допустимое напряжение в гайке на растяжение, [σ_p] = 40 МПа.

 

D_н = √((4_*22940_*1,5/(3,14_*40))+32,25² = 69,5 мм.

Расчет опорных роликов

 

Нагрузка на один винт подъемника

 

Q = G_a*K_p/n, (20)

 

где G_a – сила веса автомобиля, G_а= 38200 Н,

К_р – коэффициент неравномерности распределения силы веса по стойкам, К_р = 1,2.

 

Q = 38200*1,2/2 = 22940 Н.

 

 

Длина плеча подхвата

 

СD = 0,25*B + L (21)

 

B – ширина автомобиля, В=1,5м,

L – запас по ширине на сторону, L=0,25…0,4м.

 

СD = 0,25*1,5 + 0,3 = 0,68м

АК=(0,3…0,5)_*СD = 0,27м (22)

СК=(0,5…0,1)_*АК = 0,08 м (23)

Силы, действующие на ролики, определяют исходя из системы уравнений

 

Σ М_а = R_k*АК – Q_*CD

Σ X = R_a­ – R_k = 0 (24)

 

Откуда

 

R_k = Q_*CD/АК = 22940_*0,68/0,27 = 57724 Н (25)

 

Контактные поверхности роликов подвергаются термообработке.

Рассчитаем ролики по контактным напряжениям. Условие прочности:

 

[σ_k] < 0,418 √(q_*E_пр/r_пр), (26)

 

где Е_пр – приведенный модуль упругости,

r_пр – приведенный радиус кривизны,

q – распределенная нагрузка

Так как ролик и направляющая изготовлены из одного материала, то

 

Е₁= Е₂= Е_пр= 2_*10⁵ МПа, (27)

1/ρ_пр=1/r₁+ 1/r₂ (28)

 

r₁ – радиус ролика, диаметр роликов примем d=0,06м, тогда r₁=0,03м,

r₂ – радиус направляющей, r₂=∞

 

1/ρ_пр=1/r₁= 1/0,03 = 33,3

 

После подстановки полученных результатов в уравнение (26) получим

q < (([σ_k]_*d)/(2_*0,174_*E_*S)), (29)

 

где S – коэффициент запаса, S = 1,2…1,3,

[σ_k] – допускаемые напряжения при объемной закалке,

 

[σ_k] = 2,8_*σ_т = 2,8_*650 = 1820 МПа (30)

q < (((1820_*10⁶)²_*0,034)/(2_*0,174_*2_*10¹¹_*1,2))

q < 1348439

 

Длина ролика

 

l = R_к /q, (31)

l = 57724/1348439 = 0,04 м

 

Ролики в процессе качения по направляющим создают дополнительное усилие в винте

 

Q_g = R_k*f_*z, (32)

 

где f – коэффициент трения качения, f=0,01,

z – Число роликов в стойке, z = 2

 

Q_g = 57724_*0,01_*2 = 1154 Н

 

Уточненное усилие на винте

 

Q_у = Q + Q_g, (33)

Q_у = 37670 + 1154 = 39354 Н.

Проверка на прочность поперечной балки

 

Поперечная балка испытывает деформацию изгиба. Выполним ее проверку на прочность. Проверку производим по условию

 

σ_max=M_max^изг/W_z < [σ], (34)

 

σ_max – максимальное напряжение изгиба в балке, МПа,

M_max^изг – максимальный изгибающий момент,

W_z – осевой момент сопротивления поперечного сечения,

[σ] – допускаемое напряжение изгиба, для материала Сталь 3

[σ]=120МПа.

 

 

Рисунок 3 – Расчетная схема для проверки на прочность поперечной балки.

 

M_max^изг = R_1*l₁, (35)

 

Величину реакции R₁ найдем из системы двух уравнений

 

R₁+ R₂ = Q

R_1*l₁ = R_2*l₂, (36)

 

Решая систему уравнений, получим

R₁= Q_*l₁/(l₁+l₂), (37)

R₁= 11460 Н

M_max^изг = 11460*0,015 = 114,6 Н*м

W_z = (b_*h² – b_*h₁²)/6, (38)

 

h, h₁,b,b₁ – размеры поперечного сечении балки.

 

 

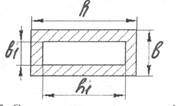
Рисунок 4 – Схема сечения поперечной балки

 

h	0,024
h1	0,02
b	0,014
b1	0,01

 

W_z = (0,024²_*0,02 – 0,014²_*0,01)/6 = 4,1_*10^{-6 м3}

 

σ_max= 114,6/4,1_*10^-6= 28 МПа < [σ] = 120 МПа

следовательно, условие прочности выполняется

 

Поделиться:

Воспользуйтесь поиском по сайту: