Определить абсолютное перемещение сечения I-I

РАСЧЕТ СТУПЕНЧАТОГО СТЕРЖНЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ РАСТЯЖЕНИИ И СЖАТИИ

 

Отчет по расчетно-проектировочной работе №1

по дисциплине сопротивление материалов

 

 

Выполнил студент группы СМ-14-2 П.А.Чернышев

 

Принял В.П.Ященко

 

Иркутск 2015

 

Цель работы:

 

1) Построить эпюру N_z;

2) Из расчета на прочность по допустимому напряжению определить безопасные размеры круглого поперечного сечения ступеней стержня (d₁ и d₂);

3) Построить эпюру σ;

4) Определить абсолютное перемещение сечения I-I.

 

 

Дано: Ступенчатый стержень круглого поперечного сечения; l = 0.4 м; F₁ = 15 кН; F₂ = 60 кН; q = 80 кН/м; материал – чугун: σ_u⁺ = 80 МПа; σ_u^- = 240 Мпа; [n] = 2; E = 1.5*10⁵ МПа (см. приложение А).

 

1 Построение эпюры N_z

Для начала необходимо будет сделать разрезы в каждой из составных частей стержня. Затем, отбросив одну из частей, заменить ее действие системой внутренних сил. В данной задаче под рассмотрение попадает продольная сила N_z.

Итак, рассмотрим каждый из участков – всего их будет 4 (см. приложение А):

 

I участок: 0 ≤ Z₁ ≤ l

 

ΣF_Z = 0: N_z(Z₁) + F₁ = 0

 

Отсюда N_z(Z₁) = - F₁ = -15 кН = const

 

II участок: 0 ≤ Z₂ ≤ l

 

ΣF_Z = 0: N_z(Z₂) + F₁ + F₂ = 0

 

Отсюда N_z(Z₂) = - F₁-F₂ = -75 кН = const

 

III участок: 0 ≤ Z₃ ≤ 3*l

 

ΣF_Z = 0: N_z(Z₃) + F₁ +F₂ – q*Z₃= 0

 

Отсюда N_z(Z₃) = - F₁ –F₂ + q*Z₃= 80*Z₃ – 75

 

В данном случае придется определить точки начала и конца графика прямой, задающей уравнение N_z.

Следовательно, N_z(Z₃ = 0) = -75 кН и N_z(Z₃ = 3*l = 1.2) = 96-75 = 21 кН

 

IV участок: 0 ≤ Z₄ ≤ 2*l

 

ΣF_Z = 0: N_z(Z₄) + F₁ +F₂ – q*(Z₄ + 1.2) = 0

 

Отсюда N_z(Z₄) = - F₁ –F₂ + q*(Z₄ + 1.2) = 80*(Z₄ + 1.2) – 75

 

Следовательно, N_z(Z₄ = 0) = 21 кН и N_z(Z₄ = 2*l = 0.8) = 85 кН = R

 

 

2 Из расчета на прочность по допустимому напряжению определить безопасные размеры круглого поперечного сечения ступеней стержня (d₁ и d₂)

Для начала необходимо рассчитать допустимое напряжение на сжатие [σ]^- и растяжение [σ]⁺ для материала, из которого изготовлен данный стержень. В данном случае это – чугун.

Следовательно, [σ]⁺ = σ_о/[n] = σ_u⁺/[n] = 80/2 = 40 МПа – на растяжение;

[σ]^- = σ_о/[n] = σ_u^-/[n] = 240/2 = 120 МПа – на сжатие.

 

Из эпюры «N_z» видно, что в первой ступени стержня – площадью А₁:

 

N_max1⁺ = 0;

|N_max1^-| = 75 кН.

 

Из эпюры «N_z» также видно, что во второй ступени стержня – площадью А₂:

 

N_max2⁺ = 85 кН;

|N_max2^-| = 75 кН.

 

Теперь определим размеры площадей поперечных сечений А₁ и А₂:

 

1 ступень:

Из условия прочности на сжатие: А₁ ≥ |N_max1^-|/[σ]^-

 

Отсюда А₁ ≥ 75*10³/(120*10⁶) = 0.625*10^-3 м²

 

В условии сказано, что данный стержень – круглого поперечного сечения. Следовательно, необходимо будет определить диаметр каждой ступени, причем, если их будет несколько, то выбрать наибольший диаметр.

 

А₁ = π* d₁²/4

 

Следовательно, d₁ = 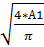= = 0.0282 м ≈ 28 мм

 

2 ступень:

Из условия прочности на растяжение: А₂^’ ≥ N_max2⁺/[σ]⁺

Из условия прочности на сжатие: А₂^’’ ≥ |N_max2^-|/[σ]^-

 

Следовательно, А₂^’ ≥ 85*10³/(40*10⁶) = 2.125*10^-3 м²

d₂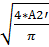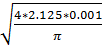^’ = = = 0.0520 м ≈ 52 мм

 

А₂^’’ ≥ 75*10³/(120*10⁶) = 0.625*10^-3 м²

d₂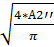^’’ = = = 0.0282 м ≈ 28 мм

 

Из этих вычислений видно, что больший диаметр – это диаметр d₂^’. Следовательно, берем d₂ = d₂^’ ≈ 52 мм.

 

3 Построить эпюру σ

Для того, чтобы построить эпюру нормальных напряжений, необходимо рассчитать достаточное количество σ, действующих на стержень, и по этим значениям построить график. Этот график должен практически совпадать с эпюрой Nz.

Для начала нужно провести несколько поперечных сечений. В данном случае их будет шесть (см. приложение А).

 

Найдем все эти напряжения по формуле σ_i = N_z/A_i:

 

1) σ_1-1 = N_1-1/A₁ = -15*10³/(0.625*10^-3) = -24 МПа – сжатие;

2) σ_2-2= N_2-2/A₁ = -75*10³/(0.625*10^-3) = -120 МПа – сжатие;

3) σ_4-4= N_4-4/A₁ = -75*10³/(0.625*10^-3) = -120 МПа = σ_2-2 – сжатие;

4) σ_3-3 = N_3-3/A₂ = -75*10³/(2.125*10^-3) = -35.294 МПа – сжатие;

5) σ_5-5= N_5-5/A₂ = 21*10³/(2.125*10^-3) = 9.882 МПа – растяжение;

6) σ_6-6= N_6-6/A₂ = 85*10³/(2.125*10^-3) = 40 МПа – растяжение.

 

Теперь нужно проверить, обеспечена ли прочность данной конструкции. Для этого сравним модули полученных напряжений с допустимым напряжением для данного материала. Должно получиться σ_max ≤ [σ].

 

Итак, для 1 ступени:

|σ_max1^-| = 120 МПа = [σ]^-

 

Для 2 ступени:

|σ_max2⁺| = 40 МПа = [σ]⁺

 

|σ_max2^-| ≈ 35.3 МПа < [σ]^-

 

Отсюда видно, что прочность для данного стержня обеспечена.

Определить абсолютное перемещение сечения I-I

Чтобы определить абсолютное перемещение δ сечения I-I (см. рисунок в приложении А), необходимо просуммировать деформации Δ участков, расположенных между этим сечением и заделкой самого стержня.

 

Определим деформацию по следующим формулам:

 

1) Δl = N_z*l/(E*A) – при N_z = const;

 

2) Δl = 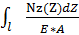– при N_z ≠ const.

 

 

δ_6-6 = 0 – заделка – стержень не перемещается

 

Так как на участке l₄ N_z ≠ const, то

 

Δl₄ = 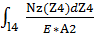= 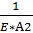* 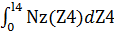= 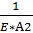* 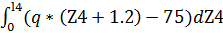= 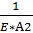* 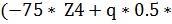(Z4+1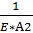.2)²)| = * (l₄+1.2)²)| = 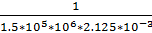*(-75*0.8+80*4*0.5-80*1.2²*0.5) = +1.33*10^-7 м

Следовательно, δ_5-5 = +1.33*10^-7 м – удлинение

 

На участке l₃ N_z ≠ const, следовательно, также

 

Δl₃ = 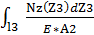= 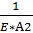* = 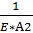* = 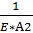* 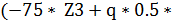(Z3)²)| = 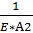* 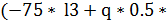(l₃)²)| = 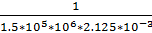*(-75*1.2+80*0.5*1.2²) = -1.02*10^-7 м – укорочение

Следовательно, δ_3-3= δ_2-2 = δ_I-I = Δl₄ + Δl₃ = 3.1*10^-8 м – удлинение

 

Отсюда видно, что абсолютное перемещение сечения I-I равно 3.1*10^-8 м, то есть в этом сечении происходит удлинение стержня (стержень будет смещаться вниз) на 3.1*10^-8 м.

 

 

Можно также рассчитать абсолютное перемещение всего стержня в целом.

 

Δl₂ = N_z2*l₂/(E*A₁) = -75*10³*0.4/(1.5*10¹¹*0.625*10^-3) = -3.2*10^-4 м – укорочение

 

Δl₁ = N_z1*l₁/(E*A₁) = -15*10³*0.4/(1.5*10¹¹*0.625*10^-3) = -6.4*10^-5 м – укорочение

 

Отсюда следует, что абсолютное перемещения всего стержня равно:

 

δ = δ_1-1 = Δl₄ + Δl₃ + Δl₂ + Δl₁ = -3,8*10^-4 м – укорочение – стержень будет двигаться вверх на 0.38 мм.

 

 

 

Приложение А

Поделиться:

Воспользуйтесь поиском по сайту: