 |
Тема 5.5 Адресная арифметика
|
|
|
|
Адресная арифметика (address arithmetic) - это способ вычисления адреса какого-либо объекта при помощи арифметических операций над указателями, а также использование указателей в операциях сравнения. Адресную арифметику также называют арифметикой над указателями (pointer arithmetic).
Согласно стандартам языка Си и Си++, при арифметике с указателями, результирующий адрес должен оставаться строго на границе единичного объекта массива (или следовать сразу за ним). Сложение или вычитание указателя сдвигает его на величину, кратную размеру того типа данных, на который он указывает. Пример. Пусть есть указатель на массив 4-байтных целых. Инкремент этого указателя приведет к увеличению его значения на 4 (размер элемента). Такой эффект часто используется для увеличения указателя для того, чтобы он указывал на следующий элемент в смежном массиве целых чисел.
Арифметика с указателями не может быть применена к указателям на неизвестные типы, поскольку неизвестные типы не имеют размера, и соответственно адрес, на который ссылается указатель, не может быть прибавлен к нему. Однако, иногда существуют нестандартные расширения компилятора, позволяющие выполнять байтовую арифметику на нетипизированных указателях (void *).
Указатели и целочисленные переменные не являются взаимозаменяемыми объектами. Константа нуль — единственное исключение из этого правила: ее можно присвоить указателю, и указатель можно сравнить с нулевой константой. Чтобы показать, что нуль — это специальное значение для указателя, вместо цифры нуль, как правило, записывают константу NULL.
Арифметика с указателями дает программисту возможность работать с разными типами одинаковым способом: за счет сложения и вычитания необходимого числа элементов вместо действительного сдвига байтов. В частности, описание языка Си явно задает равнозначность синтаксической структуры A[i], которая является i-ым элементом массива A, и *(A+i), которая представляет собой содержание элемента, на который указывает выражение A+i. Также подразумевается, что i[A] равнозначно A[i].
|
|
|
В то же время мощная арифметика с указателями может стать причиной ошибок. Адресная арифметика является сдерживающим этапом при освоении 64-битных систем, поскольку старый программный код на языках Си/Си++ может содержать большое количество ошибок связанных с использованием указателей. Более подробно с данной проблемой можно познакомиться в статье " 20 ловушек переноса Си++ - кода на 64-битную платформу".
Из-за сложностей использования указателей многие современные языки программирования высокого уровня (например, Java или C#) не разрешают прямой доступ к памяти с использованием адресов.
53. Обращение к полям. Организация и обработка списков
Линейный список - это конечная последовательность однотипных элементов (узлов), возможно, с повторениями. Количество элементов в последовательности называется длиной списка, причем длина в процессе работы программы может изменяться.
Линейный список F, состоящий из элементов D1, D2,..., Dn, записывают в виде последовательности значений заключенной в угловые скобки F=, или представляют графически (см. рис. 12).
| D1 | | D2 | | D3 | | ... | | Dn |
| Рис. 12. Изображение линейного списка. | ||||||||
Например, F1=, F2=, F3=. Длина списков F1, F2, F3 равна соответственно 3, 6, 0.
При работе со списками на практике чаще всего приходится выполнять следующие операции:
- найти элемент с заданным свойством;
- определить первый элемент в линейном списке;
- вставить дополнительный элемент до или после указанного узла;
|
|
|
- исключить определенный элемент из списка;
- упорядочить узлы линейного списка в определенном порядке.
В реальных языках программирования нет какой-либо структуры данных для представления линейного списка так, чтобы все указанные операции над ним выполнялись в одинаковой степени эффективно. Поэтому при работе с линейными списками важным является представление используемых в программе линейных списков таким образом, чтобы была обеспечена максимальная эффективность и по времени выполнения программы, и по объему требуемой памяти.
Методы хранения линейных списков разделяются на методы последовательного и связанного хранения. Рассмотрим простейшие варианты этих методов для списка с целыми значениями F=.
При последовательном хранении элементы линейного списка размещаются в массиве d фиксированных размеров, например, 100, и длина списка указывается в переменной l, т. е. в программе необходимо иметь объявления вида
float d[100]; int l;
Размер массива 100 ограничивает максимальные размеры линейного списка. Список F в массиве d формируется так:
d[0]=7; d[1]=10; l=2;
Полученный список хранится в памяти согласно схеме на рис. 13.
| l: | 2 | ||||||
| d: | 7 | 10 | ... | ||||
| [0] | [1] | [2] | [3] | [98] | [99] | ||
| Рис. 13. Последовательное хранение линейного списка. | |||||||
При связанном хранении в качестве элементов хранения используются структуры, связанные по одной из компонент в цепочку, на начало которой (первую структуру) указывает указатель dl. Структура образующая элемент хранения, должна кроме соответствующего элемента списка содержать и указатель на соседний элемент хранения.
Описание структуры и указателя в этом случае может имееть вид:
typedef struct snd /* структура элемента хранения */
{ float val; /* элемент списка */
struct snd *n; /* указатель на элемент хранения */
} DL;
DL *p; /* указатель текущего элемента */
DL *dl; /* указатель на начало списка */
Для выделения памяти под элементы хранения необходимо пользоваться функцией malloc(sizeof(DL)) или calloc(l, sizeof(DL)). Формирование списка в связанном хранении может осуществляется операторами:
|
|
|
p=malloc(sizeof(DL));
p-> val=10; p-> n=NULL;
dl=malloc(sizeof(DL));
dl-> val=7; dl-> n=p;
В последнем элементе хранения (конец списка) указатель на соседний элемент имеет значение NULL. Получаемый список изображен на рис. 14.

Рис. 14. Связное хранение линейного списка.
2. 1. 2. Операции со списками при последовательном хранении
При выборе метода хранения линейного списка следует учитывать, какие операции будут выполняться и с какой частотой, время их выполнения и объем памяти, требуемый для хранения списка.
Пусть имеется линейный список с целыми значениями и для его хранения используется массив d (с числом элементов 100), а количество элементов в списке указывается переменной l. Реализация указанных ранее операций над списком представляется следующими фрагментами программ которые используют объявления:
float d[100];
int i, j, l;
1) печать значения первого элемента (узла)
if (il) printf(" \n нет элемента" );
else printf(" d[%d]=%f ", i, d[i]);
2) удаление элемента, следующего за i-тым узлом
if (i> =l) printf(" \n нет следующего " );
l--;
for (j=i+1; j=l) printf(" \n нет соседа" );
else printf(" \n %d %d", d[i-1], d[i+1]);
4) добавление нового элемента new за i-тым узлом
if (i==l || i> l) printf(" \n нельзя добавить" );
else
{ for (j=l; j> i+1; j--) d[j+1]=d[j];
d[i+1]=new; l++;
}
5) частичное упорядочение списка с элементами К1, К2,..., Кl в
список K1', K2',..., Ks, K1, Kt",..., Kt", s+t+1=l так, чтобы K1'= K1.
{ int t=1;
float aux;
for (i=2; i=2; j--) d[j]=d[j-1];
t++;
d[i]=aux;
}
}
Схема движения индексов i, j, t и значения aux=d[i] при выполнении приведенного фрагмента программы приведена на рис. 15.
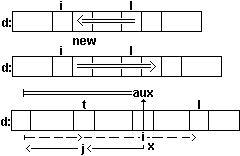
Рис. 15. Движение индексов при выполнении операций над списком в последовательном хранении.
Количество действий Q, требуемых для выполнения приведенных операций над списком, определяется соотношениями: для операций 1 и 2 - Q=1; для операций 3, 4 - Q=l; для операции 5 - Q=l*l.
Заметим, что вообще операцию 5 можно выполнить при количестве действий порядка l, а операции 3 и 4 для включения и исключения элементов в конце списка, часто встречающиеся при работе со стеками, - при количестве действий 1.
Более сложная организация операций требуется при размещении в массиве d нескольких списков, или при размещении списка без привязки его начала к первому элементу массива.
|
|
|


