Широко также применяется способ обмеров зданий и сооружений и расстояний между ними с помощью рулетки.

Способ засечек. При угловой засечке положение точки 1 определяют относительно двух пунктов съемочного обоснования А и В с помощью двух измеренных горизонтальных углов α₁ и β₁. Положение другой точки - точки 2 определяют, измеряя два других угла α₂ и β₂ (рис.7.3). Результаты измерений записывают в журнал.

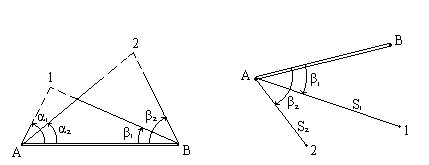
Рис.7.3 Рис.7.4

При построении плана при точках А и В с помощью транспортира строят углы α₁ и β₁ и в пересечении линий получают изображение точки 1 на плане. Аналогично находят на плане положение точки 2.

Если расстояние до точки 1 не превышает длины рулетки, положение точки 1 определяют линейной засечкой, при которой измеряют расстояния А - 1 и В - 1; при построении плана из точки А проводят дугу радиусом, равным расстоянию А - 1 в масштабе плана, а из точки В - радиусом, равным расстоянию В - 1 в масштабе плана. Точка пересечения этих дуг является изображением точки 1 на плане.

Точность измерения горизонтальных углов при угловой засечке определяется точностью их построения на плане транспортиром,т.е. порядка 10' - 15'. Допустимую ошибку измерения расстояний при линейной засечке рассчитывают по формуле:

m_s = 0,3 мм * М,

Где М - знаменатель масштаба съемки.

Полярный способ. Полярный способ съемки - это реализация полярной системы координат. Теодолит устанавливают на пункте съемочного обоснования А, принимая его за начало (полюс) местной полярной системы координат. Полярная ось совмещается с направлением на другой пункт съемочного обоснования В. Затем измеряют горизонтальный угол β₁, образованный направлением АВ и направлением на снимаемую точку 1, и расстояние S₁ от точки А до точки 1 (рис.7.4). При построении плана положение точки 1 получают, откладывая на стороне угла β₁, построенного транспортиром, расстояние S₁ в масштабе плана.

Рассчитаем среднюю квадратическую ошибку измерения углов и расстояний при полярном способе съемки, если ошибка положения точки 1 задана и равна М_p.

В полярной системе координат ошибка положение точки выражается формулой:

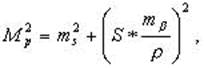(7.1)

где m_β - ошибка измерения угла β; m_s - ошибка измерения полярного расстояния.

По принципу равных влияний имеем:

m²_s = (S * m_β/ 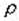)² = M² 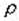/2, (7.2)

Откуда

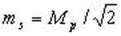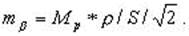и (7.3)

Пусть масштаб съемки 1:М=1:2 000, тогда М_p=0.5 мм * 2 000=1 м. При S=100 м вычисления по формулам (7.3) дают m_β=24', m_s =0.7м, m_s/S = 1/150.

Способ перпендикуляров. Способ перпендикуляров является реализацией обычной прямоугольной системы координат. Пусть линия АВ - одна из сторон теодолитного хода. Примем ее за ось l, начало координат совместим с пунктом А; ось d расположим перпендикулярно линии АВ. Положение точки 1 определяется двумя перпендикулярами l₁ и d₁ (рис.7.5), длины которых измеряют мерной лентой или рулеткой.

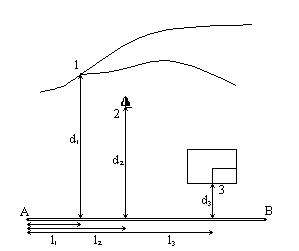
Рис.7.5

Для построения прямого угла β можно применть теодолит или эккер; иногда угол β = 90^o можно построить на глаз. Положение точки 1 на плане получают после выполнения трех операций: откладывания вдоль линии АВ длины перпендикуляра l₁, построения угла β =90^o c помощью транспортира, откладывания на стороне угла β длины второго перпендикуляра d₁.

Съемка других точек и определение их положения на плане выполняются в таком же порядке.

Ошибка положения точки М_p в способе перпендикуляров складывается из ошибки измерения перпендикуляра l, ошибки построения (или измерения) угла β = 90 ^o и ошибки измерения перпендикуляра d:

М²_p = m²_l + m_β ²/ 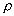² * d² + m²_d. (7.4)

По принципу равных влияний полагаем:

m²_l = m _β²/ 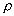² * d² = m²_d = M²_p/3. (7.5)

При М_p = 0.5 мм на плане получим 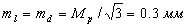в масштабе плана. Приняв ошибку построения угла m_β= 30', рассчитаем допустимую длину перпендикуляра d:

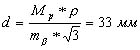
в масштабе плана при относительной ошибке его измерения:

m_d / d = 0.33 мм / 33 м = 1/110.

Для плана масштаба 1: 2 000 расчетная длина перпендикуляра d получается 66 м, а для масштаба 1: 500 - d = 16 м. В Инструкции эти величины заданы 60 м и 20 м соответственно.

Разумеется, при другом значении ошибки m_β допустимая длина перпендикуляра d будет другой. Например, строя угол β = 90^o "на глаз" (m_β = 1^o), получим d = 16 мм в масштабе плана.

При горизонтальной съемке результаты измерений углов и линий записывают в журнал. Кроме того, прямо в поле составляют схематический чертеж местности - абрис, на котором показывают все пункты съемочного обоснования, контуры, ситуацию местности, записывают результаты измерений, делают пояснительные записи.

По материалам съемки составляют и вычерчивают план участка.

Теория и устройство эккера. Эккер - прибор для построения на местности прямых углов. Эккеры бывают зеркальные и призменные. Зеркальный эккер состоит из трехгранной коробки, одна из боковых граней которой открыта (рис.7.6). К двум другим граням с внутренней стороны прикреплены зеркала. Над зеркалами вырезаны окошки. Внизу эккера имеется крючок для отвеса.

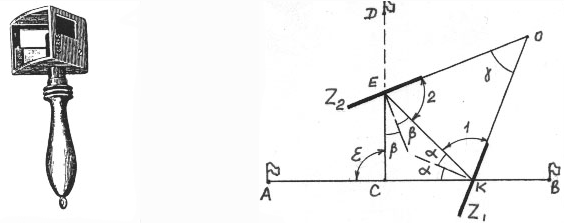
Рис.7.6 Рис.7.7

Пусть эккер установлен на линии АВ (рис.7.7). Луч от вехи А попадает в зеркало Z₁, отражается от него, падает на зеркало Z₂, отражается от него и попадает в глаз наблюдателя, составляя со своим первоначальным направлением угол ε. Теория эккера заключается в выводе формулы ε = ε (γ), где γ - угол между зеркалами.

Обозначим: α - угол падения и угол отражения на зеркале Z₁, β - угол падения и угол отражения на зеркале Z₂.

Угол ε является внешним углом треугольника СЕК, поэтому:

ε = 2 * α + 2 * β = 2 * (α + β). (7.6)

В треугольнике ЕОК:

γ = 180^o - (<1 + <2)

Но

<1 = 90^o - α, а <2 = 90^o - β,

Поэтому

γ = α + β.

Отсюда

ε = 2 * γ,

Или

γ = ε/2. (7.7)

Для того, чтобы луч составлял со своим прежним направлением угол β = 90^o, нужно, чтобы угол между зеркалами был равен 45^o.

Глаз видит изображение вехи А в зеркале Z₂ в направлении СЕ, перпендикулярном направлению АВ, а в окошко над зеркалом видно веху D, которую помощник переставляет по команде наблюдателя. Как только веха D будет находиться на линии CE, ее закрепляют.

Если вехи закреплены, то с помощью эккера можно найти на линии АВ точку С, чтобы линия DC была перпендикулярна АВ; другими словами, можно найти основание перпендикуляра, опущенного из точки D на линию АВ. Взяв в руки эккер, перемещаются по линии АВ, пока изображение вехи А в зеркале Z₂ не совпадает с направлением CD. Затем при помощи отвеса намечают на земле точку С.

Поверка эккера. Угол между зеркалами должен быть равен 45^o. Стоя в точке С, строят прямой угол, наблюдая веху А, закрепляют прямой угол первой вехой. Затем, стоя по-прежнему в точке С, строят прямой угол, наблюдая веху В, закрепляют прямой угол второй вехой. Если вехи оказались рядом, условие эккера выполняется. В противном случае намечают среднее положение, ставят веху в эту точку и юстировочными винтами зеркал изменяют угол между зеркалами до тех пор, пока изображение вехи А или В не совпадет с направлением CD. После этого поверку повторяют. Эккер считается исправным, если угол γ отличается от 45^o не больше, чем на 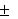2.5', тогда ошибка построения угла β = 90^o будет не больше 5'.

1Предмет и дисципланы геодезии. Задачи инженерной геодезии

Геоддезия- одна из древнейших наук. Слово- земля- разделяю, а сама наука возникла как результат практической деятельности человека по установлению границ земельных участков, строительству оросительных каналов, осушению земель. Современная геод- многогранная наука решающая сложные научные и практические задачи. Это наука об определении размеров и форм земли, об измерениях на земной поверхности для отображения её на картах и планах. Задачи геод решаются на основе измерений, выполняемых геодезическими приборами. В геод исп положения матем, физики, астрономии, картографии, и др. Геодезия подразделяется на –высшую космическую геод, топографию, фотограмметрию и прикладную геодезию, каждый из этих разделов имеет свои предмет изучения, свои задачи и методы их решения, т.е яв. Самостоятельной научно-технической дисциплиной. Несмотря на многообразие инженерных сооружений, при их проектировании и возведении решаются следующие общие задачи- получение геод данных при разработке проектов строительства сооружений инж-геод изыскания, - определение на местностиосновных осей и границ сооруж с соотв с пректом строительства, обеспеч в процессе стороит геом форм и размеров возведенного сооружения геом условий установки и наладки технологического оборудования,определение отклонения геом формы и размеров возведенного сооружения от проектных Решение современных геод задач связано с обеспечением и улучшением качества строит зданий и соружений,

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: