 |
амортизация займа, погашаемого равными срочными уплатами
|
|
|
|
Контрольная работа
по дисциплине: Финансовая математика
Вариант: 2
Выполнил: Руководитель:
Студент группы NNN-NNN ст. преп.
Nnnnnnnn N.N. Волынская О.А
Новосибирск
Задача 1
Определить простую ставку процентов, при которой первоначальный капитал в размере 10 000 руб. достигнет через 180 дней суммы 19 000 руб.
 |
Дано: Решение:
PV = 10 000 руб. Вывод формулы для простой ставки процентов: 
FV = 19 000 руб. 
t = 180 дней 
T = 360 дней
_________________ 
i -?
Ответ: простая ставка процентов равна 180%.
Задача 2
Кредит в размере 15 000 руб. выдан с 26.03 по 18.10 под простые 24% годовых. Определить размеры долга для различных вариантов начисления процентов.
Дано: Решение:
PV = 15 000 руб. Размер долга:
i = 24% = 0,24 
;
__________________ 1) «английская практика»: Т= 365 или 366 дней.
FV –? 
(дней)
I –? 
(руб.)
2) «французская практика»: T= 360 дней.
(дней)
(руб.)
3) «германская практика»: T= 360 дней.
(дня)
(руб.)
Ответ: размер долга составляет:
- согласно «английской практике»: 17 031,781 руб.;
- согласно «французской практике»: 17 060 руб.;
- согласно «английской практике»: 17 020 руб.
Задача 3
Банк объявил следующие условия выдачи ссуды на год: за I квартал ссудный процент 24%, а в каждом последующем квартале процентная ставка по ссуде увеличивается на 3%. Определить сумму к возврату в банк, если ссуда выдана на год и составляет 15 000 руб.(простые проценты)
 |
Дано: Решение:
Сумма начисленных процентов:
;
T = 1 год = 360 дней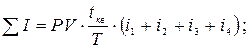 
PV = 15 000 руб. Сумма к возврату:
= 30×3 = 90 дней 
__________________ 
FV -? = 19 275 (руб.)
Ответ: сумма к возврату в банк составит 19 275 руб.
Задача 4
Договор вклада заключён сроком на 2 года и предусматривает начисление и капитализацию процентов по полугодиям. Сумма вклада 15 000 руб., годовая ставка 16%. Рассчитать сумму на счёте клиента к концу срока.
|
|
|
 |
Дано: Решение:
PV = 15 000 руб. Сумма на счёте клиента к концу срока:
n = 2 года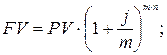 
j = 16% = 0,16 
m = 2 = 20 407,334 (руб.)
________________
FV -?
Ответ: сумма на счёте клиента к концу срока составит 20 407,334 руб.
Задача 5
Владелец векселя номинальной стоимости 19 000 руб. и сроком обращения 1 год предъявил его банку-эмитенту для учёта за 60 дней до платежа. Банк учёл его по ставке 60% годовых. Определить дисконтированную величину, то есть сумму, полученную владельцем векселя, и величину дисконта.
 |
Дано: Решение:
FV = 19 000 руб. Величина дисконта:
T = 1 год = 360 дней 
t = 60 дней 
(руб.)
n = 1 год Сумма, полученная владельцем векселя:
d = 60% = 0,6 PV = FV – D;
________________ PV = 19 000 – 1 900 = 17 100 (руб.)
D -? PV -?
Ответ: - величина дисконта равна 1 900 руб.;
- сумма, полученная владельцем векселя, равна 17 100 руб.
Задача 6
Определить значение годовой учётной ставки банка, эквивалентной ставке простых процентов 24% годовых (n = 1 год).
 |
Дано: Решение:
i = 24% = 0,24 Эквивалентная годовая учётная ставка:
n = 1 год 
;
______________ 
-?
Ответ: эквивалентная годовая учётная ставка равна 19,4%.
Задача 7
На вклады ежеквартально начисляются проценты по номинальной годовой ставке 16%. Определить сумму вклада для накопления через 1,5 года суммы 19 000 руб.
 |
Дано: Решение:
FV = 19 000 руб. Сумма вклада:
j = 16% = 0,16 
m = 4 
n = 1,5 года = 
года = 15 015,976 (руб.)
_________________
PV -?
Ответ: сумма вклада равна 15 015,976 руб.
Задача 8
Банк предлагает долгосрочные кредиты под 24% годовых с ежеквартальным начислением процентов, 26% годовых с полугодовым начислением процентов и 20% годовых с ежемесячным начислением процентов. Определить наиболее выгодный для банка вариант кредитования.
|
|
|
 |
Дано: Решение:
n = 1 год Эффективная процентная ставка:
1) m = 4 
j = 24% = 0,24 при n= 1 год: 
;
2) m = 2 
j = 26% = 0,26 
3) m = 12 
j = 20% = 0,2
_________________
-? 
-? 
-?
Ответ: выдача кредитов под 26% годовых с полугодовым начислением процентов банку выгоднее, т.к. эффективная годовая процентная ставка в этом случае больше (сумма кредита возрастает на 27,7% за год).
Задача 9
Банк выдаёт кредит под 24% годовых. Полугодовой уровень инфляции составил 3%. Определить реальную годовую ставку процентов с учётом инфляции.
 |
Дано: Решение:
n = 1 год Индекс цен:
i = 24% = 0,24 
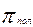= 3% = 0,03 
N = 2 Реальная годовая процентная ставка:
______________ 
-? 
Ответ: реальная годовая ставка процентов равна 16,9%.
Задача 10
Какую ставку процентов по вкладам нужно назначить, чтобы реальная доходность вклада с учётом инфляции 3% была 10% годовых?
 |
Дано: Решение:
= 3% = 0,03 Вывод формулы для процентной ставки:
n = 1 
= 10% = 0,1 
________________ 
i -?
Ответ: нужно назначить ставку процентов по вкладам, равную 13,3%.
Задача 11
Рассчитать уровень инфляции за год при ежемесячном уровне инфляции 3%.
Дано: Решение:
Индекс цен:
N = 12 месяцев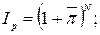 
________________ 
-? Уровень инфляции:
-? 
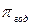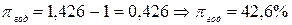
Ответ: уровень инфляции за год равен 42,6%.
Задача 12
Вклад 15 000 руб. положен в банк на полгода с ежемесячным начислением сложных процентов по номинальной ставке 72% годовых. Определить реальный доход вкладчика, если ожидаемый ежемесячный уровень инфляции составит 3%.
 |
Дано: Решение:
PV = 15 000 руб. Реальная покупательная способность вклада через
j = 72% = 0,72 определённое время:
m = 12 месяцев 
n = 6/12 года 
p = 3% = 0,03 
(руб.)
N = 6 месяцев Реальный доход вкладчика:
___________________ 
-? 
(руб.)
Ответ: реальный доход вкладчика равен 2 819,811 руб.
Задача 13
Договор аренды имущества заключён на 5 лет. Аренда уплачивается суммами S1 =19 000 руб., S2 =20 000 руб., S3 =21 000 руб. в конце 1-го, 3-го и 5-го годов. По новому графику платежей вносится две суммы: S4 =22 000 руб. в конце 2-го года и S5 в конце 4-го года. Ставка банковского процента 5%. Определить S5.
Дано: 
суммы платежей,
S1=19 000 S4 = 22 000 S2 = 20 000 S5 -? S3=21 000 руб.
|__________|__________|__________|__________|__________|
0 1 2 3 4 5 сроки платежей,
годы
|
|
|
 |
наращение дисконти-
Рование
Рис. 1. Исходный и новый графики платежей
На рис.1 отмечены: полужирным шрифтом – исходный график платежей, курсивом – новый график платежей. Моментом приведения выбран год, совпадающий с годом платежа суммы 
: 
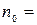4 года.
Решение:
Уравнение эквивалентности: графики платежей будут эквивалентны, если сумма приведённых на какую-либо дату (на момент приведения) платежей одного графика будет равна сумме платежей другого графика, приведённых на ту же дату при неизменной ставке процентов:
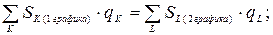
Коэффициент приведения (наращения или дисконтирования):
где: n – число лет до момента приведения:
n = n0 – ni ,
где: ni - срок i -го платежа.
при 
- коэффициент наращения;
при 
- коэффициент дисконтирования;
при 
(руб.)
Ответ: сумма второго платежа по новому графику платежей равна 38 739,875 руб.
Задача 14
Определить размер ежегодных платежей по сложной ставке 5% годовых для создания через 6 лет фонда в размере 19 000 000 руб.
Дано: Решение:
 |
i = 5% = 0,05 Размер ежегодных платежей:
n = 6 лет 
FVA = 19 000 000 руб. 
(руб.)
_____________________
R -?
Ответ: размер ежегодных платежей равен 2 793 331,894 руб.
Задача 15
Рассчитать величину фонда, который может быть сформирован за 2 года путём внесения в конце каждого года сумм 19 000 руб. Проценты на вклад начисляются по ставке 5%.
 |
Дано: Решение:
R = 19 000 руб. Величина будущего фонда:
n = 2 года 
i = 5% = 0,05 
(руб.)
____________________
FVA -?
Ответ: величина будущего фонда равна 38 950 руб.
Задача 16
Ежемесячная арендная плата за квартиру составляет 1 800 руб. Срок платежа – начало месяца. Рассчитать величину равноценного платежа, взимаемого за год вперёд. Ставка банковского депозита 48% годовых.
Дано: Решение:
 |
R = 1 800 руб. Авансовая приведённая сумма аренды:
j = 48% = 0,48 
m = 12 
n = 1 год 
________________ 
(руб.)
-?
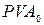Ответ: равноценный платёж, взимаемый за год вперёд, равен 17 568,858 руб.
Задача 17
Двухлетняя облигация номиналом 1 000 руб. имеет 4 полугодовых купона доходностью 20% годовых каждый. Рассчитать цену её первоначального размещения, приняв ставку сравнения 16%.
|
|
|
 |
Дано: Решение:
n = 2 года Цена первоначального размещения облигации:
N = 1 000 руб. 
m = 2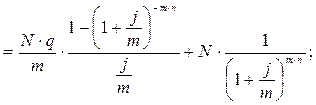 
j = 16% = 0,16 
q = 20% 
1 066,243 (руб.)
______________
P -?
Ответ: цена первоначального размещения облигации равна 1 066,243 руб.
Задача 18
Бескупонная облигация куплена на аукционе по курсу 40 и продана по курсу 58 через 90 дней. Рассчитать доходность вложения по схеме сложных и простых процентов.
Дано: Решение:
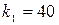1) доходность по схеме простых процентов:
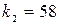
дней 
Т = 360 дней 2) доходность по схеме сложных процентов:
________________ 
Y -?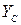 
-? 
Ответ: - доходность по схеме простых процентов равна 180%;
- доходность по схеме сложных процентов равна 342,1%.
Задача 19
Представить план амортизации 5-летнего займа в 1 500 000 руб., погашаемого:
1) равными суммами;
2) равными срочными уплатами.
Процентная ставка по займу 5%.
Дано:
i = 5% = 0,05
n = 5 лет
PVA = 1 500 000 руб.
1) амортизация займа, погашаемого равными суммами
Сумма погашения основного долга: 
(руб.)
Сумма срочной уплаты: 
Остаток долга на начало периода: 
Таблица 1
План амортизации займа, погашаемого равными суммами
| № года к | Остаток долга на начало периода  , руб.
| Сумма погашения основного долга  , руб.
| Сумма процентов  , руб.
| Сумма срочной уплаты  , руб.
|
| 1 500 000 | 300 000 | 75 000 | 375 000 | |
| 1 200 000 | 300 000 | 60 000 | 360 000 | |
| 900 000 | 300 000 | 45 000 | 345 000 | |
| 600 000 | 300 000 | 30 000 | 330 000 | |
| 300 000 | 300 000 | 15 000 | 315 000 | |
| Итого: | Х | 1 500 000 | 225 000 | 1 725 000 |
амортизация займа, погашаемого равными срочными уплатами
Срочный платёж:
(руб.);
Сумма процентов: 
Погасительный платёж: 
Остаток долга на начало периода: 
Таблица 2
План амортизации займа, погашаемого равными срочными уплатами
| № года к | Остаток долга на начало периода
, руб.
| Остаток долга на конец периода,
 , руб.
| Срочный платёж R, руб. | Сумма процентов  , руб.
| Погаситель-ный платёж  , руб.
|
| 1 500 000,00 | 1 228 537,80 | 346 462,20 | 75 000,00 | 271 462,20 | |
| 1 228 537,80 | 943 502,49 | 346 462,20 | 61 426,89 | 285 035,31 | |
| 943 502,49 | 644 215,42 | 346 462,20 | 47 175,13 | 299 287,07 | |
| 644 215,42 | 329 963,99 | 346 462,20 | 32 210,77 | 314 251,43 | |
| 329 963,99 | -0,01 | 346 462,20 | 16 498,20 | 329 964,00 | |
| Итого: | Х | Х | 1 732 311,00 | 232 310,99 | 1 500 000,01 |
|
|
|
