 |
Основные определения и формулы.
|
|
|
|
План.
- Матрицы и определители:
- умножение матриц;
- вычисление определителей 2-го и 3-го порядка
- Координаты вектора в некотором базисе.
- Скалярное произведение:
- понятие скалярного произведения векторов;
- свойства скалярного произведения векторов;
- геометрический и физический смысл скалярного произведения;
- длина вектора, угол между векторами;
- ортонормированный базис
 ;
; - формула скалярного произведения в координатах.
- Векторное произведение векторов:
- понятие векторного произведения;
- свойства векторного произведения;
- геометрический смысл векторного произведения;
- формула векторного произведения в координатах.
- Смешанное произведение:
- понятие смешанного произведения;
- свойства смешанного произведения;
- геометрический смысл смешанного произведения;
- формула смешанного произведения в координатах.
Задачи.
1.1. Выполнить умножение матриц:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 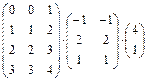 . .
|
1.2. Вычислить определители 2-го порядка:
а)  ; ;
| б)  . .
|
1.3. Вычислить определители 3-го порядка разными способами:
а)  ; ;
| б)  . .
|
1.4. Точки K и L служат серединами сторон BC и CD параллелограмма ABCD. Полагая  и
и 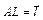 , выразить через векторы
, выразить через векторы  и
и 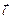 векторы
векторы  и
и  .
.
1.5. Из точки O выходят два вектора  и
и 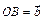 . Найти какой-нибудь вектор
. Найти какой-нибудь вектор  , идущий по биссектрисе
, идущий по биссектрисе  .
.
1.6. Найти угол  при вершине равнобедренного треугольника, зная, что медианы, проведенные из концов основания этого треугольника, взаимно перпендикулярны.
при вершине равнобедренного треугольника, зная, что медианы, проведенные из концов основания этого треугольника, взаимно перпендикулярны.
1.7. Зная векторы  и
и  , найти:
, найти:
а)  ; б)
; б)  .
.
1.8. Вычислить векторное произведение  и площадь параллелограмма, построенного на векторах
и площадь параллелограмма, построенного на векторах  ,
,  .
.
1.9. Показать, что если три вектора  ,
,  ,
, 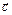 не коллинеарны, то из равенств
не коллинеарны, то из равенств  вытекает соотношение
вытекает соотношение  и обратно.
и обратно.
1.10. Доказать:
а) тождество Лагранжа («БАЦ минус ЦАБ»)  ;
;
|
|
|
б) тождество Якоби  .
.
Домашнее задание.
1.11. Выполнить умножение матриц:
а)  ; ;
| б)  ; ;
| в)  . .
|
1.12. Вычислить определители:
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
1.13. В ∆  даны длины его сторон
даны длины его сторон  ,
,  ,
,  . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  и
и  .
.
1.14. Дан равносторонний треугольник  , у которого длины сторон равны
, у которого длины сторон равны  . Вычислить выражение
. Вычислить выражение  .
.
1.15. В ∆  проведены медианы
проведены медианы  ,
,  ,
,  . Вычислить выражение
. Вычислить выражение 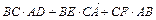 .
.
1.16. Вычислить скалярное произведение векторов  и
и  , заданных своими координатами, и определить угол между ними, если
, заданных своими координатами, и определить угол между ними, если  ,
,  .
.
1.17. Вычислить векторное произведение  и площадь параллелограмма, построенного на векторах
и площадь параллелограмма, построенного на векторах  ,
,  .
.
1.18. Доказать, что  .
.
1.19. Показать, что если  , то векторы
, то векторы  ,
,  ,
, 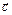 компланарны.
компланарны.
Дополнительное задание.
1.20. Найти  и
и  , если
, если 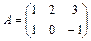 ,
,  .
.
1.21 Решить уравнение:  .
.
1.22. Доказать, что сумма векторов идущих из центра правильного многоугольника к его вершинам, равна  .
.
1.23. Доказать тождество:  .
.
1.24. Две тройки векторов 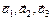 и
и  называются взаимными, если векторы этих троек связаны соотношениями:
называются взаимными, если векторы этих троек связаны соотношениями:  для всех
для всех  и
и  при
при  . Используя операции скалярного и векторного умножения, найти векторы
. Используя операции скалярного и векторного умножения, найти векторы  тройки, взаимной тройке векторов
тройки, взаимной тройке векторов  .
.
Основные определения и формулы.
| Наименование | Обозначение, формула |
| Скалярное произведение | |
| Определение скалярного произведения двух векторов |  , , 
|
| Скалярное произведение в декартовых координатах | 
|
| Скалярный квадрат | 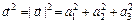
|
Свойства:
1) коммутативность (переместительное)
2) ассоциативность (сочетательное) относительно скалярного множителя  3) дистрибутивность (распределительное)
3) дистрибутивность (распределительное)
|


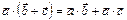
|
| Условие ортогональности двух векторов | 
|
Приложения:
1) Угол между векторами
2)Проекция вектора  на вектор на вектор 
|


|
| Векторное произведение | |
| Определение векторного произведения двух векторов |  , такой что:
1) , такой что:
1) 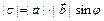 , ,  ;
2) ;
2) 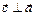 , ,  ;
3) ;
3)  - правая тройка векторов - правая тройка векторов
|
| Векторное произведение в декартовых координатах | 
|
Свойства:
1) антикоммутативность (антипереместительное)
2) ассоциативность (сочетательное) относительно скалярного множителя  3) дистрибутивность (распределительное)
3) дистрибутивность (распределительное)
|


 , ,

|
| Условие коллинеарности двух ненулевых векторов | 
|
| Тождество Лагранжа («БАЦ минус ЦАБ») |  , ,

|
Приложение:
Площадь параллелограмма, построенного на векторах  и и 
|

|
| Смешанное произведение | |
| Определение смешанного произведения трех векторов | 
|
| Смешанное произведение в декартовых координатах | 
|
Свойства:
1) изменение знака при перестановке двух сомножителей
2) не меняется при циклической перестановке множителей
3) векторы  , ,  , , 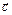 образуют
- правую тройку, если
- левую тройку, если образуют
- правую тройку, если
- левую тройку, если
|




|
| Условие компланарности трех векторов |  компланарны компланарны
|
Приложение:
Объем параллелепипеда, построенного на векторах  , ,  , , 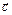
|
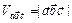
|
Из одной точки проведены три некомпланарных вектора  ,
,  ,
, 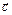 . Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна вектору
. Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна вектору  .
.
|
|
|
Доказать, что если векторы  ,
, 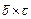 ,
,  компланарны, то они коллинеарны.
компланарны, то они коллинеарны.
Доказать тождество:  .
.
Пусть вектор  разложен по двум неколлинеарным векторам
разложен по двум неколлинеарным векторам  и
и 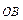 , а именно:
, а именно:  . Доказать, что точки A, B, C будут лежать на одной прямой в том и только том случае, когда
. Доказать, что точки A, B, C будут лежать на одной прямой в том и только том случае, когда 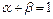 .
.
На сторонах CA и CB (или их продолжениях) треугольника ABC взяты соответственно точки  и
и  , которые делят эти стороны в данных отношениях:
, которые делят эти стороны в данных отношениях:  ,
,  . Доказать, что радиус-вектор
. Доказать, что радиус-вектор  точки пересечения прямых
точки пересечения прямых  и
и  имеет вид
имеет вид 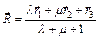 , где
, где  ,
,  ,
,  - радиус-векторы точек A, B, C.
- радиус-векторы точек A, B, C.
Семинар 2. Скалярное, векторное, смешанное произведения векторов.
План.
- Скалярное произведение:
- понятие скалярного произведения векторов;
- свойства скалярного произведения векторов;
- геометрический и физический смысл скалярного произведения;
- длина вектора, угол между векторами;
- ортонормированный базис
 ;
; - формула скалярного произведения в координатах.
- Векторное произведение векторов:
- понятие векторного произведения;
- свойства векторного произведения;
- геометрический смысл векторного произведения;
- формула векторного произведения в координатах.
- Смешанное произведение:
- понятие смешанного произведения;
- свойства смешанного произведения;
- геометрический смысл смешанного произведения;
- формула смешанного произведения в координатах.
|
|
|
|
|
|


