 |
Глава 2. Приведенная форма
|
|
|
|
Приведенная форма эконометрической модели. Если эконометрическая модель является полной, то существует обратная матрица. Благодаря этому можно решить систему уравнений относительно совместно зависимых переменных, умножая (4) и (5) слева на
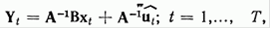 (4)
(4)
 (5)
(5)
Форма эконометрической модели, задаваемой в виде (6) или (7), называется приведенной. Если мы в (12.9) и (12.10) воспользуемся обозначением
 (6)
(6)
а также
 (7)
(7)
то приведенную форму модели можно записать более просто:
 (6)
(6)
или
 (7)
(7)
Представим матричное уравнение подробно в виде отдельных уравнений
 (8)
(8)
Из (8) видно, что совместно зависимые переменные являются линейными функциями от предопределенных и возмущающих переменных. В равенстве находит отражение тот факт, что коэффициенты уравнений модели в приведенной форме представляют собой конгломерат структурных параметров. Для этого построим следующие матрицы:

Уравнения модели в приведенной форме примут вид:

Из (12.16) видно, что коэффициенты уравнений в приведенной форме являются комбинациями всех элементов матрицы А (всех структурных коэффициентов совместно зависимых переменных) и элементов столбцов матрицы В (структурных коэффициентов соответствующих предопределенных переменных во всех структурных уравнениях). Например, коэффициент си модели в приведенной форме при переменной в первом уравнении составлен из всех элементов матрицы А и структурных коэффициентов переменной в обоих структурных уравнениях - элементов первого столбца матрицы В.
Уравнения в приведенной форме из-за сложности представления коэффициентов теряют по отношению к предопределенным переменным свою автономность, которая характерна для структурных уравнений. Если, например, из-за изменения коэффициента изменится си, то неизбежно изменится и так как содержится в нем. Но, с другой стороны, каждое уравнение в приведенной форме характеризуется определенной автономностью относительно совместно зависимых переменных, так как каждое из этих уравнений содержит текущее значение только одной эндогенной переменной, которое выражается как функция всех предопределенных переменных. Итак, очевидно, что взаимосвязи совместно зависимых переменных при переходе от структурной формы к приведенной распространяются на предопределенные переменные, а также на возмущения. Если мы сравним, например, первые уравнения (12.16), то в модели приведенной формы (12.16) объясняется всеми предопределенными переменными модели, т. е. а также остатками обоих структурных уравнений в Но в первое уравнение модели (12.16) не входит.
|
|
|
На основе высказанных соображений становится очевидной интерпретация уравнений в приведенной форме. Коэффициенты этих уравнений отражают непосредственное и косвенное влияние предопределенных переменных на совместно зависимые переменные (общий эффект), в то время как структурные параметры выражают только непосредственное влияние предопределенных переменных (частичный эффект). В этом смысле экономическая интерпретация коэффициентов уравнений в приведенной форме реалистичнее, чем интерпретация структурных параметров. Модель в приведенной форме построена как бы с учетом предпосылки, что «другие объясняющие переменные не изменяются», так как в этой модели каждая совместно зависимая переменная объясняется только предопределенными переменными.
Каждое уравнение в приведенной форме представляет собой множественную регрессию. К уравнениям непосредственно применим метод наименьших квадратов для оценивания неизвестных коэффициентов приведенной формы. Модель в приведенной форме используется для прогнозирования. Если оценки коэффициентов приведенной формы и значения предопределенных переменных приходятся на период времени прогноза, то по модели находят прогнозные значения совместно зависимых переменных. И напротив, структурная форма для прогноза непригодна, так как в каждом структурном уравнении содержится несколько совместно зависимых переменных, для которых не могут быть указаны значения на прогнозируемый период времени, поскольку они еще только подлежат оценке. Однако приведенная форма модели имеет и существенный недостаток. От количественно оцененной модели в приведенной форме не во всех случаях можно перейти к модели в структурной форме, в то время как по заданной в численном виде структурной форме может быть всегда определена приведенная форма.
|
|
|
Итак, мы убедились, что как структурная, так и приведенная формы выполняют свои специфические функции, позволяют решать определенные задачи и имеют свои достоинства и недостатки. Поэтому регрессионную модель обычно представляют в обеих формах, а затем их интерпретируют.
При построении других форм регрессионной модели исходят из структурной формы и исследуют вид матрицы А.
Модель из взаимозависимых переменных. Модель из взаимозависимых переменных представляется в виде системы структурных уравнений, в которых переменные одновременно удовлетворяют нескольким равенствам. Следовательно, переменные являются многосторонне зависимыми. Матрица А структурных параметров совместно зависимых переменных может быть любого вида. Матрица дисперсий и ковариаций возмущающих переменных также может иметь любой вид:

Заключение
Эконометрика возникла на базе междисциплинарного подхода к изучению экономики. По϶ᴛᴏму эконометрику можно представить как комбинацию трёх наук - экономической теории, математической и экономической статистики и математики. Помимо ϶ᴛᴏго, на современном этапе развития науки одним из важнейших факторов развития эконометрики стало развитие компьютерных технологий и специальных пакетов прикладных программ.
Анализ экономических процессов и явлений в эконометрике осуществляется с помощью математических моделей, построенных на эмпирических данных.
|
|
|
Моделью называется материальный или мысленно представляемый объект, замещающий в процессе исследования объект-оригинал таким образом, что его непосредственное изучение дает новые знания об объекте-оригинале. Модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на базе реальной статистической информации. Применение метода моделирования вызвано тем, что большинство объектов (или проблем, ᴏᴛʜᴏϲᴙщихся к данным объектам) непосредственно исследовать или совершенно невозможно, или подобное исследование требует много времени и средств.
Важно знать, что большинство эконометрических методов и приёмов исследования экономических явлений и процессов позаимствованы из математической статистики. При этом в применении данных методов в эконометрике существует определённая специфика. По причине того, что практически все экономические показатели будут случайными величинами, а не результатами контролируемого эксперимента, были разработаны определённые усовершенствования и модификации методов, кᴏᴛᴏᴩые не применяются в математической статистике.
По причине того, что экономические данные могут быть измерены с ошибкой, в эконометрике были разработаны специальные методы анализа, позволяющие устранить или снизить влияние данных ошибок на полученные результаты.
Исходя из всего выше сказанного, мы приходим к выводу, что эконометрика исследует различные экономические закономерности, установленные экономической теорией, с помощью методов математической и экономической статистики.
Список используемой литературы
1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2002. - 344 с.
. Практикум по эконометрике: Учебн. пособие / Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2003. - 192 с.
. Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. - Казань: ТИСБИ, 2002. - 56 с.
. Доугерти К. Введение в эконометрику: Пер. с англ. - М.: ИНФРА-М, 1999. - 402 с.
|
|
|


