Вычисление кеплеровых элементов

Кеплеровы элементы орбиты

Материал из Википедии — свободной энциклопедии

(перенаправлено с «Наклонение орбиты»)

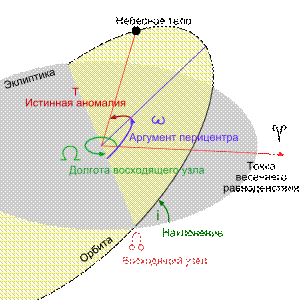
Кеплеровские элементы орбиты, включая аргумент перицентра (рис.1)

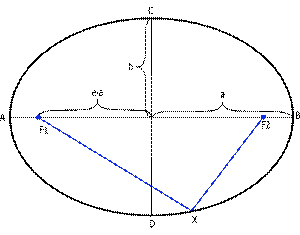
Части эллипса (рис.2)

Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:

• большая полуось (),
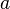• эксцентриситет (),
• наклонение (),
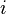• аргумент перицентра (),
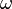• долгота восходящего узла (),
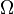• средняя аномалия ().

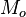Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию плоскости орбиты по отношению к базовой системе координат, шестой — положение тела на орбите.

Содержание

• 1 Большая полуось
• 2 Эксцентриситет
• 3 Наклонение
• 4 Аргумент перицентра
• 5 Долгота восходящего узла
• 6 Средняя аномалия
• 7 Вычисление кеплеровых элементов
• 8 Примечания
• 9 См. также

Большая полуось

Большая полуось — это половина главной оси эллипса (обозначена на рис.2 как a). В астрономии характеризует среднее расстояние небесного тела от фокуса.^{[ источник не указан 607 дней ]}

Эксцентриситет

Эксцентрисите́т (обозначается «» или «ε») — числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.^[1] Эксцентриситет характеризует «сжатость» орбиты. Он выражается по формуле:

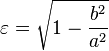, где 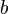— малая полуось (см. рис.2)

Можно разделить внешний вид орбиты на пять групп:

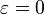• — окружность
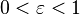• — эллипс
• — парабола
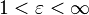• — гипербола
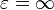• — прямая (вырожденный случай)

Наклонение

A — Объект
B — Центральный объект
C — Плоскость отсчёта
D — Плоскость орбиты
i — Наклонение

Наклонение орбиты (накло́н орбиты, накло́нность орбиты, наклоне́ние) небесного тела — это угол между плоскостью его орбиты и плоскостью отсчёта (базовой плоскостью).

Обычно обозначается буквой i (от англ. inclination). Наклонение измеряется в угловых градусах, минутах и секундах.

Если 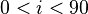°, то движение небесного тела называется прямым ^[2].

Если 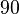° °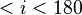, то движение небесного тела называется обратным.

• В применении к Солнечной системе, за плоскость отсчёта обычно выбирают плоскость орбиты Земли (плоскость эклиптики). Плоскости орбит других планет Солнечной системы и Луны отклоняются от плоскости эклиптики лишь на несколько градусов.
• Для искусственных спутников Земли за плоскость отсчёта обычно выбирают плоскость экватора Земли.
• Для спутников других планет Солнечной системы за плоскость отсчёта обычно выбирают плоскость экватора соответствующей планеты.
• Для экзопланет и двойных звёзд за плоскость отсчёта принимают картинную плоскость.

Зная наклонение двух орбит к одной плоскости отсчёта и долготы их восходящих узлов, можно вычислить угол между плоскостями этих двух орбит — их взаимное наклонение, по формуле косинуса угла.

Аргумент перицентра

Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.

При исследовании экзопланет и двойных звёзд в качестве базовой используют картинную плоскость — плоскость, проходящую через звезду и перпендикулярную лучу наблюдения звезды с Земли. Орбита экзопланеты, в общем случае случайным образом ориентированная относительно наблюдателя, пересекает эту плоскость в двух точках. Точка, где планета пересекает картинную плоскость, приближаясь к наблюдателю, считается восходящим узлом орбиты, а точка, где планета пересекает картинную плоскость, удаляясь от наблюдателя, считается нисходящим узлом. В этом случае аргумент перицентра отсчитывается из притягивающего центра против часовой стрелки.

Обозначается ().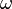

Долгота восходящего узла

Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемый для математического описания ориентации плоскости орбиты относительно базовой плоскости. Определяет угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, базовая плоскость — эклиптика, а нулевая точка — Первая точка Овна (точка весеннего равноденствия); угол измеряется от направления на нулевую точку против часовой стрелки.

Восходящий узел обозначается ☊, или Ω.

Средняя аномалия

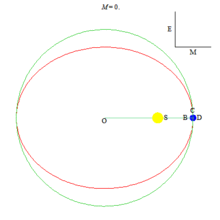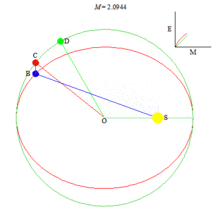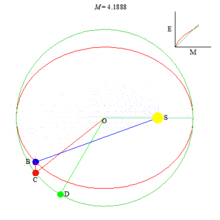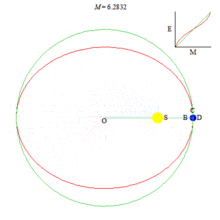
Анимация, иллюстрирующая истинную аномалию, эксцентрическую аномалию, среднюю аномалию и решение уравнения Кеплера.

Аномалии (рис.3)

Средняя аномалия для тела, движущегося по невозмущённой орбите — произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом, средняя аномалия есть угловое расстояние от перицентра гипотетического тела, движущегося с постоянной угловой скоростью, равной среднему движению.

Обозначается буквой 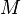(от англ. mean anomaly)

В звёздной динамике средняя аномалия 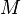вычисляется по следующим формулам:

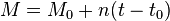
где:

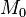· — средняя аномалия на эпоху ,

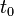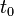· — начальная эпоха,

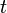· — эпоха, на которую производятся вычисления, и

· — среднее движение.

Либо через уравнение Кеплера:

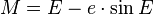
где:

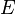• — это эксцентрическая аномалия ( 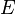на рис.3),
• — это эксцентриситет.

Вычисление кеплеровых элементов

Рассмотрим следующую задачу: пусть имеется невозмущённое движение и известны вектор положения и вектор скорости на момент времени 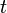. Найдём кеплеровы элементы орбиты.

Прежде всего, вычислим большую полуось:

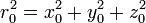
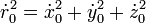
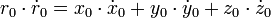
По интегралу энергии:

(1) 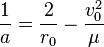, где μ — гравитационный параметр, равный произведению гравитационной постоянной на массу небесного тела; для Земли μ = 3,986005·10⁵ км³/c², для Солнца μ = 1,32712438·10¹¹ км³/c².

Следовательно, по формуле (1) находим .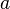

Примечания

1. ↑ А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
2. ↑ То есть, объект движется вокруг Солнца в том же направлении, что и Земля

См. также

• Элементы орбиты

[показать] Небесная механика

 

[скрыть] Иоганн Кеплер
Научные достижения	Гипотеза Кеплера • Законы Кеплера • Кеплеровы элементы орбиты • Треугольник Кеплера • Уравнение Кеплера • Тело Кеплера — Пуансо • Сверхновая Кеплера
Публикации	Mysterium Cosmographicum (1596) • Astronomia nova (1609) • Epitome Astronomiae Copernicanae (1617–21) • Harmonices Mundi (1619) • Рудольфинские таблицы (1627) • Somnium (1634)
Семья	Катарина Кеплер (мать) • Якоб Барч (зять)

Категории:

• Небесная механика
• Системы небесных координат
• Орбиты

 

Поделиться:

Воспользуйтесь поиском по сайту: