 |
Верхний центральный показатель линейной системы
|
|
|
|
Верхний центральный показатель некоторой линейной системы
Курсовая работа
Исполнитель:
Студентка группы М-42
Лукьянович А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
Зверева Т.Е.
Гомель 2006
Содержание
Введение
1. Верхнее центральное число семейства функций
2. Верхний центральный показатель линейной системы
Заключение
Список использованной литературы
Введение
Цель данной курсовой работы - найти верхний центральный показатель системы
где k=0, 1, 2,….
Из определения верхнего центрального показателя диагональной системы следует, что верхний центральный показатель рассматриваемой системы совпадает с верхним центральным числом конечного семейства
, где 
Таким образом, главная задача курсовой работы - найти верхнее центральное число соответствующего конечного семейства
.
Верхнее центральное число семейства функций
Рассмотрим какое-либо семейство кусочно-непрерывных и равномерно ограниченных функций:
, 
,
зависящее от параметра x непрерывно в том смысле, что из 
следует
равномерно по крайней мере на каждом конечном отрезке [0,t]. Параметр x может пробегать некоторое компактное (в частности, конечное) множество.
Определение 1 [1, с.103]: ограниченная измеримая функция R (t) называется верхней функцией для семейства P, если все функции этого семейства равномерно не превосходят в интегральном смысле функцию R (t):
,
т.е. если
,
где 
- константа, общая для всех 
и 
, но, вообще говоря, зависящая от выбора R и 
>0.
Определение 2 [1, с.103]: совокупность всех верхних функций называется верхним классом семейства P (обозначим через N=N (P)).
|
|
|
Определение 3 [1, с.534 ]: число
называется верхним средним значением функции p (t).
Определение 4 [1, с.103]: число
где 
- верхнее среднее значение функции R (t), называется верхним центральным числом семейства P. Оно будет обозначаться также 
.
Докажем следующее утверждение: если семейство состоит из двух функций 
и при этом 
, то верхний класс семейства P можно считать состоящим из одной функции 
, и 
.
Неравенство означает, что
и для любого 
существует такая константа 
, что
Или
(1)
Аналогичное неравенство для функции очевидно
.
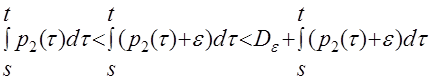Согласно определения 1 является верхней функцией для семейства
.
Докажем равенство
.
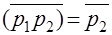Если существует такая верхняя функция 
, что 
для всех 
, то эта функция одна образует верхний класс и 
[1, с.104].
Найдем такую верхнюю функцию 
, что 
.
Рассмотрим интегралы
Разделим последнее неравенство на (t-s), получим
Устремив 
и вычислив верхний предел при , получим
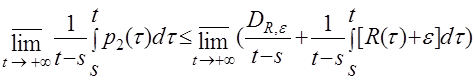
или
Итак, имеем
Значит, 
.
Так как 
- верхняя функция, то 
.
Верхний центральный показатель линейной системы
Пусть дана система
(2)
и 
- ее решение.
Рассмотрим семейство функций
, 
, 
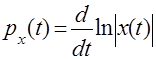Определение 5 [1, с.116]: Функция R (t) называется верхней для системы (2), если она ограничена, измерима и осуществляет оценку
,
Где
- норма матрицы Коши линейной системы.
Совокупность 
всех верхних функций называется верхним классом системы (2), а число
верхним центральным показателем линейной системы.
Диагональная система
имеет матрицу Коши
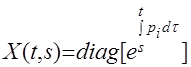
с нормой
.
Поэтому верхний центральный показатель диагональной системы совпадает с верхним центральным числом конечного семейства P={ 
} [1, с.118].
Найдем верхний центральный показатель следующей системы
|
|
|
(3)
где k=0, 1, 2,….
Верхний центральный показатель системы (3) совпадает с верхним центральным числом конечного семейства
, где 
Найдем верхнее центральное число семейства
.
Согласно утверждения, доказанного в пункте1: если семейство состоит из двух функций 
и при этом 
, то
.
Проверим, осуществляется ли оценка . (4)
Подставляя 
в (1), получим
Или
Оценка (4) осуществляется, следовательно, 
.
Вычислим верхнее среднее значение функции 
.
По определению 3 имеем
.
Вычисляя интеграл
,
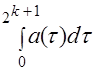Получим
Так как 
, то 
Таким образом, верхнее центральное число семейства
,
где 
, равно 0, следовательно, верхний центральный показатель системы (3) также равен 0.
Заключение
Таким образом, мы выяснили, что если семейство состоит из двух функций 
и при этом 
, то 
; верхний центральный показатель рассмотренной системы совпадает с верхним центральным числом конечного семейства 
и равен 0.
Список использованной литературы
1. Б.Ф. Былов и др. "Теория показателей Ляпунова" - М.: Наука, 1966 г., 564 с.
|
|
|
