 |
Методика и техника эксперимента
|
|
|
|
Физическим маятником называется твёрдое тело, способное совершать колебания вокруг неподвижной оси О, не проходящей через центр инерции С. На него действуют сила тяжести m g и сила реакции со стороны оси.
Поскольку все точки маятника движутся по окружностям, центры которых расположены на одной оси, его движения является вращательным. При отклонении маятника от положения равновесия на угол j возникает вращательный момент M силы тяжести
,
где m – масса маятника, d - расстояние от оси вращения до центра масс системы. Знак “минус” обусловлен противоположной направленностью j и M. Момент силы реакции оси равен нулю, т.к. линия действия силы проходит через ось вращения.
Применим основной закон динамики вращательного движения:
,
в котором 
- угловое ускорение, J - момент инерции маятника. Преобразуя его к виду
и учитывая, что при малых углах отклонения маятника 
, получим дифференциальное уравнение колебательного процесса:
.
Как нетрудно увидеть путем прямой подстановки, решение данного уравнения имеет вид:
,
т.е. угол j изменяется по гармоническому закону, тело совершает гармонические колебания с циклической частотой 
и периодом
. (1)
Приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Формула для периода колебаний математического маятника имеет вид:
. (2)
Из сравнения выражений (1) и (2) видно, что приведенная длина физического маятника равна:
. (3)
Отложим от точки подвеса О вдоль прямой ОС отрезок ОО ¢, длина которого равна приведенной длине физического маятника l. Точка О ¢ называется центром качания. Центр качания можно определить как точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.
|
|
|
По теореме Штейнера
.
Подставив это выражение в формулу (3), получим следующее выражение для приведенной длины:
. (4)
Отсюда следует, что, во-первых, l > d, т.е. точка подвеса О и центр качания О ¢ лежат по разные стороны от масс С и, во-вторых, что всем точкам
подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина, а, следовательно, один и тот же период колебаний Т.
Точка подвеса и центр качания являются взаимными или сопряженными точками в следующем смысле. Если маятник подвесить за центр качания О ¢, то его период не изменится и прежняя точка подвеса О сделается новым центром качания. Это положение называется теоремой Гюйгенса.
Пусть О ¢ является точкой подвеса. Тогда приведенная длина в соответствии с (4) будет
.
Из рисунка видно, что 
, а в соответствии с (3) 
. Подставив это значение в предыдущую формулу, получим:
,
т.е. приведенная длина, а следовательно, период колебаний физического маятника остались без изменений.
Теорема Гюйгенса используется в оборотном маятнике для измерений ускорения свободного падения. Физический оборотный маятник, используемый в данной работе, состоит из металлического стержня, на котором жестко закреплены две опорные призмы О и О ¢, и три чечевицы. Две из них находятся на концах стержня, их положение не изменяется при проведении эксперимента. Третья подвижная чечевица А находится между опорными призмами. Путем перемещения чечевицы А можно менять расстояние d между точкой подвеса О и центром тяжести С, а также расстояние d ¢ между центром тяжести С и центром качания О ¢.
Перемещением этой чечевицы достигают совпадения периодов колебаний маятника, когда точками подвеса являются ребра опорных призм О и О ¢. Поэтому при совпадении периодов колебаний расстояние между ними дает приведенную длину физического маятника l. Измеряя период колебаний Т, можно вычислить ускорение g по формуле, полученной из (2):
|
|
|
.
Используя формулу для периода колебаний 
, окончательно находим:
. (5)
Из (3) можно выразить момент инерции маятника относительно оси подвеса О: 
. Собственный момент инерции маятника относительно оси, проходящей через его центр масс J 0, связан с J по теореме Штейнера:
,
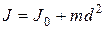откуда
или
. (6)
|
|
|
