 |
Построение векторной диаграммы
|
|
|
|
Исследование трехфазной цепи при соединении приемников в треугольник
Цель – исследование трех однофазных приемников, соединенных в треугольник при различных режимах работы цепи.
Краткие теоретические сведения
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи бывают несимметричными, очень важно на практике обеспечить независимость режима работы отдельных фаз. Кроме четырехпроводной цепи подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника треугольником. Соединением в треугольник называется соединение, когда конец одной фазы соединяется с началом другой, образуя замкнутый контур. Полученные узлы присоединяют к соответствующим началам фаз генератора линейными проводами (рис. 19).
В треугольник могут соединяться фазы трансформаторов, электродвигателей, фазы осветительной нагрузки и т. д. При соединении фаз приемников с сопротивлениями 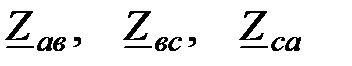 в треугольник каждая фаза включается на линейное напряжение источника. Поэтому фазные напряжения
в треугольник каждая фаза включается на линейное напряжение источника. Поэтому фазные напряжения 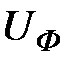 равны линейным напряжениям
равны линейным напряжениям 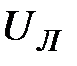 , т.е.
, т.е.  .
.
Фазные токи 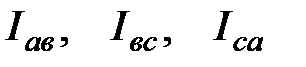 определяются по формулам
определяются по формулам
 ;
; 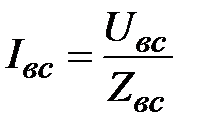 ;
;  .
.
Линейные токи 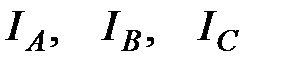 определяются по фазным токам из уравнений, составленных по первому закону Кирхгофа для узлов а, в, с (см. рис. 19).
определяются по фазным токам из уравнений, составленных по первому закону Кирхгофа для узлов а, в, с (см. рис. 19).
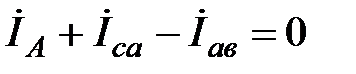 ,
,  ;
;
 ,
, 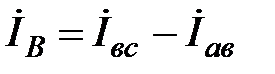 ;
;
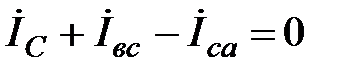 ,
, 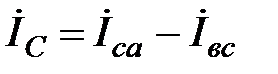 .
.
Рис. 19. Схема трехпроводной трехфазной цепи при соединении приемников в треугольник
Из уравнений (28) следует, что любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом. Векторы линейных токов 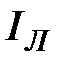 можно определить из векторной диаграммы, построенной на основании уравнений (21), для чисто активной нагрузки, например, осветительной (рис. 20).
можно определить из векторной диаграммы, построенной на основании уравнений (21), для чисто активной нагрузки, например, осветительной (рис. 20).
|
|
|
При симметричной нагрузке
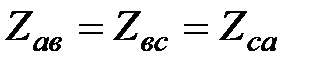 ; ; 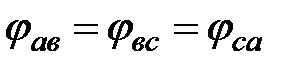 ; ; 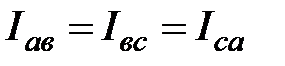 .
При этом линейный .
При этом линейный  и фазный и фазный 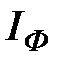 токи связаны числовым соотношением, которое можно определить из заштрихованного треугольника (см. рис. 20). токи связаны числовым соотношением, которое можно определить из заштрихованного треугольника (см. рис. 20).
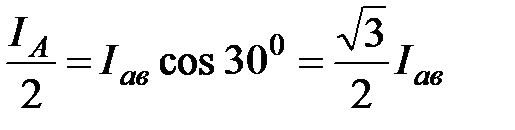 ; ;
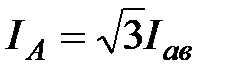 ; ;
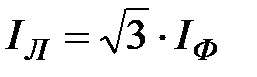 . .
|
При несимметричной нагрузке – при изменении сопротивления одной из фаз, режим работы других фаз останется неизменным, так как сохраняется постоянство напряжений на фазах нагрузки, что является важной особенностью соединения фаз приемника треугольником. Поэтому схему соединения треугольником используют для включения несимметричных однофазных приемников, например, осветительных приборов в трехпроводную осветительную сеть.
В зависимости от условий работы нагрузки целесообразно изменять способ соединения фаз – переключать со звезды на треугольник и обратно, при этом линейный ток нагрузки изменяется в три раза.
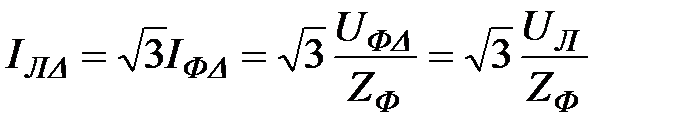 ;
;
 , тогда отношение
, тогда отношение  , т. е.
, т. е. 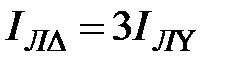 .
.
Активную мощность каждой фазы можно определить по формуле
 ,
,
а всей цепи – как  .
.
Активная мощность симметричного трехфазного приемника, как и при соединении фаз звездой: 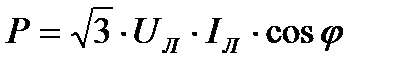 .
.
Реактивная мощность каждой фазы определяется по формуле
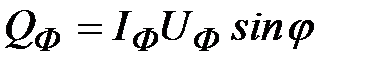 .
.
Задание
1. Исследовать трехфазную цепь при соединении приемников в треугольник для симметричной и несимметричной нагрузок.
2. Для всех режимов определить мощность, потребляемую каждой фазой и всей цепью.
3. Для симметричного режима определить отношение  .
.
4. Построить векторные диаграммы напряжений и токов.
Построение векторной диаграммы
1. Выбрать масштаб для тока 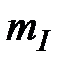 и для напряжения
и для напряжения 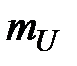 .
.
2. Построить равносторонний треугольник фазных (линейных) напряжений приемника Uав, Uвс, Uса (см. рис. 20).
3. С учетом характера нагрузки (активная, индуктивная, емкостная) строятся векторы фазных токов. При индуктивной нагрузке вектор фазного тока отстает от своего напряжения на 90о, при емкостной – вектор фазного тока опережает напряжение на 90о, при чисто активной нагрузке фазный ток совпадает по направлению со своим напряжением  .
.
|
|
|
4. На основании уравнений (21) построить векторы линейных токов.
|
|
|


